Buzz
Bài toán Königsberg diễn ra tại thành phố cổ Königsberg, nay là Kaliningrad. Ban đầu, Königsberg là một thành phố của Vương quốc Phổ, được thành lập năm 1255. Sau đó, nó trở thành thủ đô của Đức, và cuối cùng là địa điểm được quân đội Liên Xô chiếm vào năm 1945.
Câu chuyện bắt đầu vào thế kỷ 18, tại thị trấn Königsberg nằm bên bờ sông Pregel có 7 chiếc cầu, chia thành phố thành 4 vùng. Người dân Kaliningrad gặp khó khăn khi phải di chuyển qua các cầu này vì sự phức tạp của cấu trúc. Một câu đố đã được đưa ra: liệu có cách nào để đi qua tất cả 7 cây cầu mà không lặp lại bất kỳ cây cầu nào (mỗi cây cầu chỉ được qua một lần), từ bất kỳ điểm nào đến bất kỳ điểm nào. Câu đố này thu hút sự quan tâm của nhiều người, thậm chí có người đến Kaliningrad để tìm lời giải, nhưng cho đến nay vẫn chưa có ai giải quyết được.Euler và bài toán
Thực tế, Königsberg không cách xa Petersburg, nơi mà nhà toán học lỗi lạc Leonhard Euler sinh sống. Tuy nhiên, tại sao Euler lại quan tâm và dành thời gian cho một câu đố dường như không liên quan đến toán học như thế? Vào thời điểm đó, Euler đã bận rộn với nhiều dự án khác nhau, ước tính ông đã xuất bản hơn 500 cuốn sách và bản thảo trong cả cuộc đời. Chỉ trong năm 1775, trung bình mỗi tuần ông hoàn thành một bài báo khoa học. Trong suốt cuộc đời, ông nghiên cứu nhiều lĩnh vực khác nhau ngoài toán học như cơ học, quang học, thiên văn học, và thuỷ động lực học. Vì vậy, không có gì ngạc nhiên khi ông ban đầu coi câu đố này là không đáng chú ý.
Tuy vậy, Euler vẫn cảm thấy hứng thú với bài toán này. Trong một lá thư gửi cho nhà toán học và kỹ sư người Ý Giovanni Marioni cùng năm, Euler viết: “Câu đố này có vẻ đơn giản, nhưng tôi nghĩ rằng nó đáng được quan tâm khi cả hình học, đại số và phương pháp đếm đều không thể giải quyết được nó.” Euler tin rằng câu đố này liên quan đến một chủ đề mà Gottfried Wilhelm Leibniz từng thảo luận và đã bày tỏ mong muốn được nghiên cứu cùng, được gọi là geometria situs (hình học vị trí), sau này được biết đến là toán học Topo. Đây là tiền thân của lý thuyết đồ thị, một lĩnh vực toán học quan trọng trong tương lai. Chính nhờ vào bài toán này, Euler đã mở ra một nhánh mới cho toán học tổ hợp và lời giải của ông được xem là định lý đầu tiên của lý thuyết đồ thị, được gọi là đường đi Euler.
Chứng minh của Euler
Trong một bài báo xuất bản năm 1741, Euler đã giải quyết vấn đề của 7 cây cầu Königsberg và đề xuất lời giải tổng quát cho loại bài toán này, bất kể số lượng vùng đất hay số lượng cây cầu. Bài báo này được gọi là Giải vấn đề liên quan đến geometriam situs gồm 21 phần, mô tả và phân tích của Euler cho dạng bài toán như thế này.
Trong bài báo này, Euler cũng thừa nhận rằng bài toán này liên quan đến hình học, nhưng không phải là loại hình học thời điểm đó mà là một loại mới hoàn toàn, hình học vị trí. Ngoài ra, ông cũng cho rằng có thể liệt kê tất cả các con đường có thể trong bài toán, nhưng điều đó rất tốn thời gian và không hiệu quả khi áp dụng vào những bài toán lớn hơn cùng dạng. Vì vậy, Euler quyết định chọn một phương pháp khác.
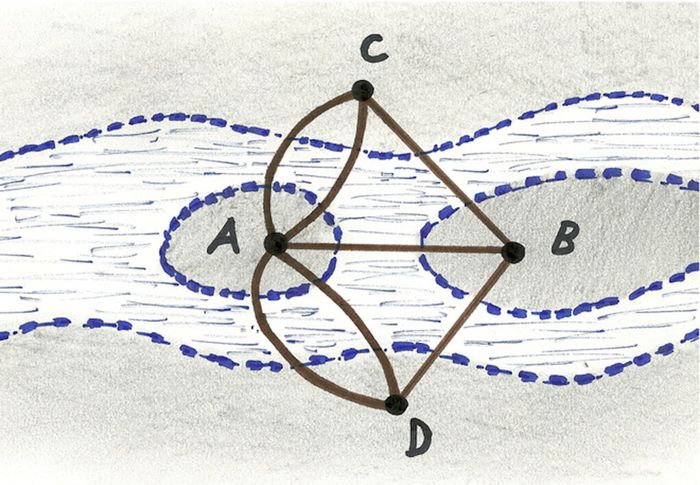
Euler đã đơn giản hóa và thay thế tất cả các chi tiết đất, cù lao bằng điểm và thay cầu bằng đoạn nối, sau đó ông thu được một đồ thị vô hướng như sau. Cách biểu diễn này bằng điểm và đoạn nối đã mở ra đường cho sự phát triển của lý thuyết đồ thị sau này.
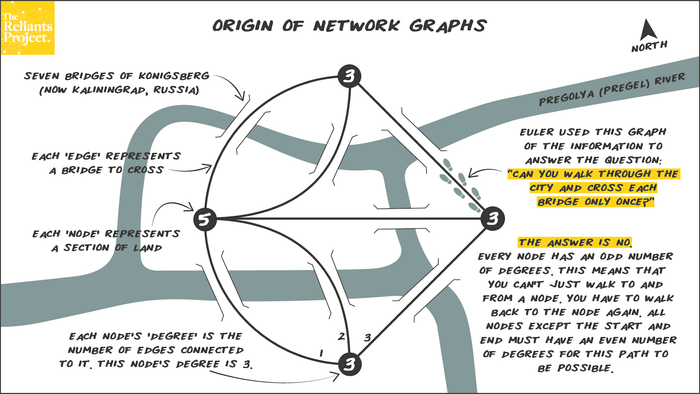
Quay trở lại với bài toán, khi đi qua một vùng, người ta phải băng qua một cây cầu và rời đi bằng cây cầu khác. Vì vậy, luôn tồn tại một cặp cạnh đến và đi. Điều này dẫn đến bậc của đồ thị phải là số chẵn (bậc của mỗi đỉnh bằng số cạnh kết nối với nó), ví dụ như A có bậc là 5, B là 3,… Sau đó, Euler đã nhận thấy và đưa ra định lý rằng một đồ thị có đường đi qua tất cả các cạnh và mỗi cạnh chỉ đi qua một lần gọi là đường đi Euler, khi và chỉ khi:
- Chỉ có thể tồn tại 2 đỉnh bắt đầu và kết thúc có bậc lẻ, còn các đỉnh khác trong đồ thị G phải là bậc chẵn.
- Đồ thị vô hướng liên thông G là đồ thị Euler khi và chỉ khi mọi đỉnh của G đều có bậc chẵn.
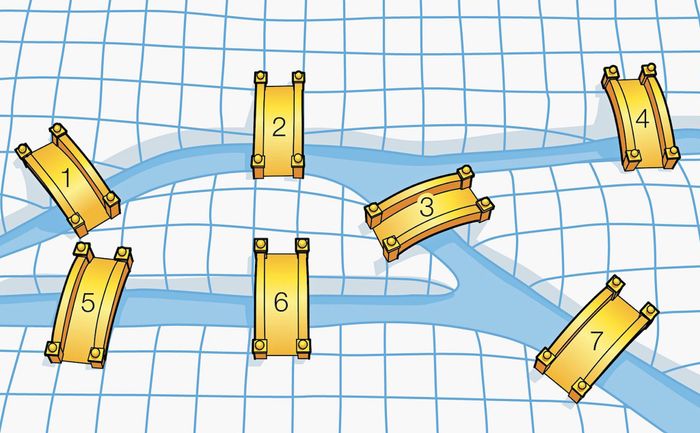
Trong bài toán 7 cây cầu này, có đến 4 nút có bậc lẻ, vì vậy điều này không thể tồn tại. Euler cũng đã chỉ ra rằng có thể sửa đổi câu đố này bằng cách xây thêm hoặc loại bỏ một cây cầu phù hợp. Thực tế, điều này đã xảy ra vào năm 1875, khi người dân thành phố Königsberg quyết định xây dựng thêm một cây cầu mới giữa 2 đỉnh và C, làm tăng số bậc của 2 nút này lên 4, điều này đảm bảo điều kiện của đường đi Euler, và bài toán sẽ có lời giải.
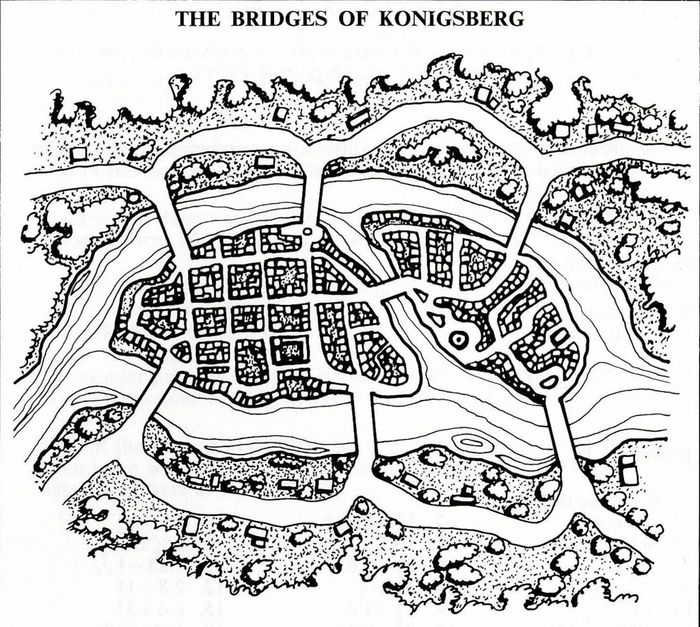
Khi ngắm nhìn lại lịch sử, chúng ta không thể không nhớ đến Königsberg - một thành phố từng nổi tiếng với bài toán bảy cây cầu. Nhưng số phận của nó lại đầy bi thương. Tận năm 1944, bom Anh đã vơ vét mọi dấu tích, và năm 1945, quân Nga bao vây, khiến thành phố chìm trong bi kịch. Ngày nay, dù đã thay đổi nhiều, Königsberg vẫn là biểu tượng của một thời kỳ đầy hy vọng và đau thương.
