Bất bình đẳng

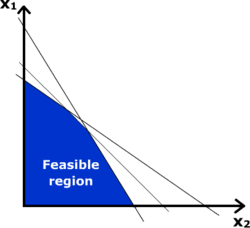
Trong toán học, một bất bình đẳng (tiếng Anh: Inequality) là phát biểu về mối quan hệ thứ tự và kích thước giữa hai số hoặc các biểu thức toán học. Nó thể hiện sự khác biệt về giá trị, do đó được gọi là bất bình đẳng, trái ngược với đẳng thức. Thường được dùng để so sánh hai số trên trục số dựa trên giá trị của chúng. Các ký hiệu khác nhau được dùng để biểu thị các bất bình đẳng khác nhau, chẳng hạn như:

• có nghĩa là a nhỏ hơn b.
• $a>b$ có nghĩa là a lớn hơn b.

Trong cả hai tình huống trên, a không bằng b. Những bất bình đẳng này được gọi là bất bình đẳng chặt chẽ, biểu thị rằng a hoàn toàn nhỏ hơn hoặc lớn hơn b.

Ngoài ra, còn có các bất bình đẳng không chặt chẽ:

• $a\le <!--\; \le \; -->b$ có nghĩa là a nhỏ hơn hoặc bằng b.
• $a\ge <!--\; \ge \; -->b$ có nghĩa là a lớn hơn hoặc bằng b.
• $|a|\ge <!--\; \ge \; -->a$ có nghĩa là giá trị tuyệt đối của a lớn hơn hoặc bằng a.

Quan hệ không lớn hơn (tức nhỏ hơn hoặc bằng) có thể được ký hiệu là a >/ b, trong đó ký hiệu > (lớn hơn) bị cắt ngang bởi dấu gạch chéo (nghĩa là không). Tương tự, quan hệ không nhỏ hơn (tức lớn hơn hoặc bằng) được biểu diễn là a ≮ b.

Một dạng bất bình đẳng khác là a ≠ b, có nghĩa là a không bằng b. Bất bình đẳng này đôi khi được xem là một dạng bất bình đẳng chặt chẽ. Nó không chỉ rõ rằng a lớn hơn b hoặc ngược lại, cũng không chỉ rõ rằng a bằng b. Nó chỉ đơn thuần thể hiện rằng giá trị của a khác giá trị của b.

Trong kỹ thuật, một số ký hiệu ít phổ biến hơn được dùng để chỉ ra rằng một giá trị 'lớn hơn nhiều' hoặc 'nhỏ hơn nhiều' so với giá trị khác:

• Ký hiệu a ≪ b cho thấy rằng a nhỏ hơn nhiều so với b.
• Ký hiệu a ≫ b chỉ ra rằng a lớn hơn nhiều so với b.

Các ký hiệu a, b trong bất đẳng thức có thể là các biểu thức chứa biến. Dưới đây, chúng ta sẽ chỉ xem xét các bất đẳng thức với các biến thuộc tập số thực hoặc các tập con của nó.

Nếu một bất đẳng thức đúng với mọi giá trị của các biến liên quan, thì đó được gọi là bất đẳng thức tuyệt đối hay không điều kiện. Ngược lại, nếu bất đẳng thức chỉ đúng với một số giá trị nhất định của các biến, và có thể không đúng hoặc bị đảo chiều với các giá trị khác, thì nó được gọi là bất đẳng thức có điều kiện. Một bất đẳng thức vẫn giữ đúng nếu cả hai vế của nó được cộng hoặc trừ cùng một giá trị, hoặc nhân hoặc chia với cùng một số dương. Tuy nhiên, bất đẳng thức sẽ bị đảo chiều nếu cả hai vế được nhân hoặc chia với một số âm.

Các bài toán thường gặp liên quan đến bất đẳng thức bao gồm

1. Chứng minh rằng bất đẳng thức đúng với các giá trị của các biến thuộc một tập hợp cho trước, đó là bài toán chứng minh bất đẳng thức.
2. Tìm tập các giá trị của biến sao cho bất đẳng thức đúng, đó là bài toán giải bất phương trình.
3. Xác định giá trị lớn nhất hoặc nhỏ nhất của một biểu thức với một hoặc nhiều biến, đây được gọi là tìm cực trị.

Các đặc điểm

Các đặc tính của bất bình đẳng bao gồm:

Đảo ngược

Các quan hệ < và >, ≤ và ≥ là các dạng đảo ngược của nhau, tức là với mọi số thực a và b:

• và $b>a$ là tương đương.
• $a\le <!--\; \le \; -->b$ và $b⪈<!--\; ⪈\; -->a$ là tương đương.

Đặc điểm bắc cầu

Tính chất bắc cầu của bất đẳng thức có thể được diễn đạt như sau:

• Với mọi số thực a, b,c:
  • Nếu $a>b$ và $b>c$
    thì $a>c$
  • Nếu và thì

Các tính chất liên quan đến phép cộng và phép trừ

Các đặc điểm liên quan đến phép cộng và phép trừ được nêu như sau:

Phép cộng và phép trừ với cùng một số thực giữ nguyên mối quan hệ thứ tự trên tập số thực. Cụ thể là

• Với mọi số thực a, b và c:
  • Nếu $a>b$ thì $a+c>b+c$ và $a-<!--\; -\; -->c>b-<!--\; -\; -->c$
  • Nếu thì và

Các tính chất liên quan đến phép nhân và phép chia

Các đặc điểm liên quan đến phép nhân và phép chia được trình bày như sau:

Phép nhân (hoặc chia) với một số thực dương giữ nguyên mối quan hệ thứ tự trên tập số thực, trong khi phép nhân (hoặc chia) với một số thực âm sẽ đảo ngược mối quan hệ thứ tự trên tập số thực. Cụ thể:

• Với mọi số thực a, b và c:
  • Nếu c là số dương và $a>b$ thì $a\times <!--\; \times \; -->c>b\times <!--\; \times \; -->c$ và $a/c>b/c$
  • Nếu c là số dương và thì và
  • Nếu c là số âm và $a>b$ thì và
  • Nếu c là số âm và thì $a\times <!--\; \times \; -->c>b\times <!--\; \times \; -->c$ và $a/c>b/c$

Áp dụng hàm đơn điệu lên hai vế của bất đẳng thức

Dựa vào định nghĩa của hàm đơn điệu (tăng hoặc giảm), chúng ta có thể biến hai vế của một bất đẳng thức thành các biến của một hàm đơn điệu tăng nghiêm ngặt mà bất đẳng thức vẫn đúng. Ngược lại, nếu ta áp dụng một hàm đơn điệu giảm nghiêm ngặt, thì phải đảo ngược chiều của bất đẳng thức ban đầu để đạt được một bất đẳng thức đúng.

Điều này có nghĩa là:

1. Nếu bất đẳng thức không nghiêm ngặt a ≤ b (hoặc a ≥ b) và
   1. $f\left(x\right)$ là hàm đơn điệu tăng thì$f\left(a\right)$ ≤ $f\left(b\right)$ hoặc $f\left(a\right)$ ≥ $f\left(b\right)$ nếu bất đẳng thức ban đầu là a ≥ b.
   2. Nếu $f\left(x\right)$ là hàm đơn điệu giảm thì$f\left(a\right)$ ≥ $f\left(b\right)$ hoặc $f\left(a\right)$ ≤ $f\left(b\right)$ nếu bất đẳng thức ban đầu là a ≥ b.

Những ký hiệu bất đẳng thức kép

Ký hiệu a<b<c diễn tả rằng a nhỏ hơn b và b nhỏ hơn c, từ đó suy ra a nhỏ hơn c. Tương tự, chúng ta có thể cộng hoặc trừ cùng một số vào tất cả các số hạng trong bất đẳng thức này, hoặc nhân/chia tất cả các số hạng với cùng một số khác. Tuy nhiên, cần lưu ý rằng nếu số đó là âm, chiều của bất đẳng thức có thể bị đảo ngược. Ví dụ, a < b + e < c tương đương với a - e < b < c - e.

Ký hiệu ghép nối có thể mở rộng với nhiều số hạng hơn. Ví dụ, a₁ ≤ a₂ ≤ ... ≤ a_n biểu thị rằng a_i ≤ a_i+1 với i = 1, 2, ..., n-1. Theo tính chất bắc cầu, điều này đồng nghĩa với việc a_i ≤ a_j cho mọi 1 ≤ i ≤ j ≤ n.

Ký hiệu ghép nối cũng có thể xuất hiện trong các bất đẳng thức ngược chiều, tức là các bất đẳng thức riêng biệt cho từng cặp số hạng kế tiếp. Ví dụ, a < b > c ≤ d có nghĩa là a < b, b > c và c ≤ d. Tuy nhiên, trong toán học, kiểu ký hiệu này ít được sử dụng và chỉ một số ngôn ngữ lập trình như Python mới hỗ trợ kiểu ký hiệu này.

Các bất đẳng thức nổi bật

Khi không thể hoặc gặp khó khăn trong việc tìm công thức chính xác cho các đại lượng, các nhà toán học thường sử dụng bất đẳng thức để xác định khoảng giá trị mà các đại lượng này có thể đạt được. Dưới đây là một số bất đẳng thức phổ biến và có tên gọi đặc trưng:

• Bất đẳng thức Azuma
• Bất đẳng thức Bernoulli
• Bất đẳng thức Boole
• Bất đẳng thức Cauchy-Schwarz
• Bất đẳng thức cộng Chebyshev
• Bất đẳng thức Chernoff
• Bất đẳng thức Cramer-Rao
• Bất đẳng thức Hoeffding
• Bất đẳng thức Holder
• Bất đẳng thức Jensen
• Bất đẳng thức Markov
• Bất đẳng thức Minkowski
• Bất đẳng thức Nesbitt
• Bất đẳng thức Pedoe
• Bất đẳng thức tam giác
• Bất đẳng thức trung bình cộng và trung bình nhân

• Quan hệ (toán học)
• Tập được sắp bộ phận
• Bất phương trình

• Hardy, G., Littlewood J.E., Polya, G. (1999). Bất đẳng thức. Thư viện Toán học Cambridge, Nhà xuất bản Cambridge University Press. ISBN 0521052068.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
• Beckenbach, E.F., Bellman, R. (1975). Giới thiệu về Bất đẳng thức. Random House Inc. ISBN 0394015592.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
• Drachman, Byron C., Cloud, Michael J. (1998). Bất đẳng thức: Ứng dụng trong Kỹ thuật. Springer-Verlag. ISBN 0387984046.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)