Sáng tạo bởi hai nhà toán học người Ba Lan Stefan Banach (1892-1945) và Alfred Tarski (1901-1983) vào năm 1924.
Năm 1924, Stefan Banach và Alfred Tarski phát hiện một hiện tượng toán học đầy bí ẩn: 'chia một quả bóng thành một số phần, rồi ghép các phần đó lại để tạo ra hai quả bóng giống hệt nhau với quả ban đầu'.

Nhiều người tự hỏi: 'Làm sao điều đó có thể xảy ra?'. Tuy nhiên, ngày nay định lý này đã được chứng minh và gọi là 'định lý Banach-Tarski'.
Tuy nhiên, định lý này không áp dụng được trong thế giới thực. 'Phân đoạn' ở đây chỉ là một phương pháp toán học và không thể thực hiện trong thực tế.

Vậy tại sao lúc đó hai nhà khoa học này lại nghĩ ra nghịch lý như vậy? Bối cảnh là đã có một cuộc tranh luận trong cộng đồng toán học vào thời điểm đó về việc liệu “Tiên đề lựa chọn” có đúng hay không. Đây là một chủ đề toán học rất khó nên chúng ta hãy phác thảo ngắn gọn nó ở đây.
Tiên đề lựa chọn là một trong những tiên đề trong “lý thuyết tập hợp” và được nhà toán học người Đức Ernst Zermelo (1871-1953) xuất bản năm 1904. Lý thuyết tập hợp đề cập đến trường sử dụng số, công thức, ký hiệu, v.v. để kiểm tra các thuộc tính của 'tập hợp' chứa các phần tử khác nhau.
Nội dung của tiên đề lựa chọn là “khi một tập hợp gồm nhiều tập con (một tập hợp chỉ gồm một phần các phần tử của tập hợp đó) thì từ mỗi tập hợp con có thể chọn ra một phần tử để tạo thành một tập hợp mới”. Nhiều người sẽ coi điều này là đương nhiên. Georg Cantor, nhà toán học người Đức, người đã xây dựng nền tảng của lý thuyết tập hợp, cũng tin rằng tiên đề lựa chọn là một điều đã cho. Trong thực tế, khi số lượng tập hợp con bị giới hạn thì việc chọn các phần tử từ mỗi tập hợp con là không có vấn đề gì.
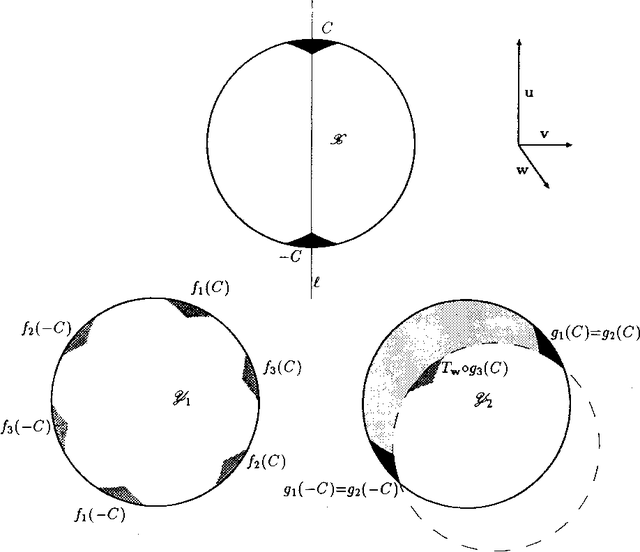
Tuy nhiên, nếu số lượng tập hợp con là vô hạn thì thao tác chọn phần tử cũng đòi hỏi số lần vô hạn. Do đó, thao tác lựa chọn phần tử không thể hoàn thành và không rõ liệu một tập hợp mới có thể được hình thành hay không. Kết quả là cuộc tranh luận về việc liệu tiên đề lựa chọn có đúng hay không đã tiếp tục kéo dài trong nhiều năm.
Trong bối cảnh này, nếu sử dụng tiên đề lựa chọn, có thể rút ra kết quả dẫn đến nghịch lý Banach-Tarski. Khi phân đoạn quả bóng (chọn một phần các điểm tạo nên quả bóng để tạo thành một tập hợp mới), bạn cần sử dụng tiên đề chọn lọc.
Sau đó, cuộc tranh luận về tiên đề lựa chọn tiếp tục nóng lên và cuối cùng kết thúc vào năm 1938. Nhà toán học gốc Séc Kurt Gödel (1906-1978), nổi tiếng với “Định lý không đầy đủ”, đã chứng minh rằng “ngay cả khi tiên đề lựa chọn là đúng thì nó cũng sẽ không dẫn đến những mâu thuẫn mới trong lý thuyết tập hợp”. Dựa trên điều này, 'Nghịch lý Banach-Tarski' cuối cùng đã chính thức trở thành 'Định lý Banach-Tarski'.
Tham khảo: Zhihu
