Có thể Bạn Tính Số Pi bằng cách Vẽ Hình Tròn?

Nếu bạn nghĩ về nó, pi thực sự kỳ quặc. Số vô tỷ này xuất hiện ở những nơi kỳ cục nhất. Nếu bạn đưa một khối lượng đi lại trên một sợi dây, có một pi ở đó. Nó xuất hiện trong nguyên lý không chắc chắn Heisenberg, lý thuyết tương đối chung của Einstein và sự tương tác giữa hai điện tích.

Tất nhiên, hầu hết mọi người liên kết pi với hình tròn. Điều đó là dễ hiểu, vì định nghĩa cơ bản nhất của pi là tỉ lệ giữa chu vi và đường kính của một hình tròn:

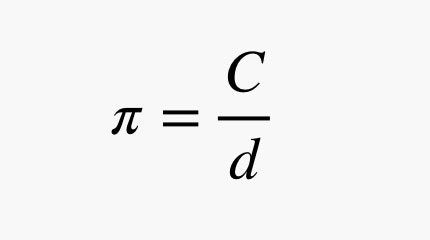
Bây giờ đến phần quan trọng. Hôm nay, như bạn có thể biết, là Ngày Pi. Tại sao lại là hôm nay? Bởi vì đó là ngày 14 tháng 3—đúng, 3/14—và 3.14 là giá trị của pi đến hai chữ số thập phân. Tất nhiên, con số thực tế tiếp tục với vô số chữ số thập phân: 3.14159265359 … và cứ thế, mãi mãi. Đó là lý do tại sao nó được gọi là vô tỷ.

Tôi nên thêm rằng Hoa Kỳ hầu như là nơi duy nhất sử dụng định dạng ngày tháng/năm trung-endian. Nếu bạn chọn định dạng little-endian là ngày/tháng/năm, thì hôm nay là 14/3—rõ ràng là không phải là pi. (Trong trường hợp đó, tôi đề xuất ngày 22 tháng 7, vì tỷ lệ 7/22 là một sự ước lượng khá tốt cho pi.)

Dù sao, cách truyền thống của tôi để chào mừng Ngày Pi là tìm một cách mới mỗi năm để tính giá trị số cho pi. Đó chỉ là điều tôi làm. Tôi đã làm điều này đã khá lâu nay, vì vậy đây là một số cách tôi thích nhất:

• Tìm pi bằng số ngẫu nhiên (và Python)
• Xác định giá trị của pi bằng cách một khối lượng dao động trên một lò xo
• Thực sự đo chu vi và đường kính của những hình tròn thực tế

Tôi có thêm nhiều bài viết về Ngày Pi ở đây. Nhưng bây giờ hãy thử một cách mới. Hãy xem chúng ta có thể đến gần pi bằng cách vẽ một hình tròn.

Dưới đây là cách nó sẽ hoạt động. Bạn vẽ một hình tròn. Từ hình tròn đó, bạn có thể xác định cả chu vi và bán kính. Sau đó, giá trị của pi sẽ là chu vi chia cho hai lần bán kính. Đơn giản, phải không?

Oh, nhưng những nếu hình tròn của bạn không hoàn hảo? Ý tôi là, ai lại vẽ hình tròn hoàn hảo chứ? Hãy tưởng tượng rằng hình tròn không hoàn hảo này thực sự là một loạt các điểm rời rạc được kết nối bằng các đoạn đường. Nếu bạn phóng to lên một phần nó, nó có thể trông như thế này:

Bây giờ tôi có thể tìm khoảng cách giữa từng điểm kế tiếp bằng công thức sau:

Đối với chu vi tổng cộng, tôi có thể chỉ cần cộng tất cả những khoảng cách này. Điều đó nên hoạt động rất tốt. Nhưng còn về bán kính? Hãy giả sử rằng có một trung tâm biết đến của hình tròn không hoàn hảo. Trong trường hợp đó, tôi có thể tính toán bán kính như là khoảng cách trung bình từ trung tâm đến tất cả các điểm tạo thành hình tròn.

Vì vậy, tôi đã viết một đoạn mã Python để thực hiện phép toán này. Hãy thử nghiệm nó dưới đây! Hãy vẽ hình tròn tốt nhất bạn có thể bằng cách kéo quả bóng màu vàng xung quanh quả bóng trắng ở giữa. Sau khi bạn đi xung quanh hết, chương trình sẽ tính toán chu vi và bán kính của hình tròn của bạn—và từ đó, giá trị của pi. Bạn có thể xem mã bằng cách nhấp vào biểu tượng bút. Để chạy nó lại, hãy nhấp vào nút Phát.

Tôi sẽ trung thực—điều này có thể tốt hơn. Mọi thứ luôn trở nên hơi lộn xộn khi bạn thêm tương tác chuột vào VPython (ít nhất là với tôi), vì vậy đây là một bộ vấn đề độc đáo. Nhưng tôi thích giữ mọi thứ càng đơn giản càng tốt.

Bây giờ là Thách thức Ngày Pi. (Vâng, tôi tự đặt ra thách thức cho mình.) Bạn có thể vẽ một hình tròn cho giá trị pi được tính toán gần với 3.14159265359 không? Bạn có thể nhận đúng bao nhiêu chữ số thập phân? Bạn có thể có giá trị tốt hơn so với bạn bè không? Hãy xem nào!

• Cách tự làm nước rửa tay
• Singapore đã sẵn sàng cho Covid-19—các quốc gia khác, hãy chú ý
• Liệu việc đặt đồ ăn có đạo đức trong đại dịch không?
• Không thể ngừng chạm vào khuôn mặt? Khoa học có một số lý thuyết về điều đó
• Mẹo làm việc từ nhà mà không mất trí
• Đọc tất cả bài viết về coronavirus của chúng tôi tại đây