Bí quyết tính diện tích hình chóp & minh họa độc đáo

Buzz

Nội dung bài viết

I. Hình chóp là gì? Hình chóp đều là gì?

1. Định nghĩa về hình chóp

2. Đặc điểm của hình chóp

3. Hình chóp đều là gì?

II. Công thức tính diện tích hình chóp

1. Công thức tính diện tích xung quanh hình chóp

2. Công thức tính diện tích toàn phần hình chóp

III. Ví dụ minh họa

Xem thêm

Đọc tóm tắt

- Hình chóp là hình đa diện, đáy là đa giác lồi, mặt bên hình tam giác, và đỉnh không nằm trên đáy.
- Có nhiều loại hình chóp khác nhau, được đặt tên theo hình đáy.
- Đường cao của hình chóp là đường thẳng đi qua đỉnh và vuông góc với mặt đáy.
- Hình chóp đều có đáy là đa giác đều với các tam giác bên bằng nhau.
- Công thức tính diện tích xung quanh hình chóp là Sxq = p.d.
- Công thức tính diện tích toàn phần hình chóp là Stp = Sxq + Sđáy.
- Ví dụ minh họa về tính diện tích hình chóp trong bài toán thực tế.

Để đắp đầy kiến thức thiếu sót về hình chóp, hãy cùng Mytour khám phá những công thức tính diện tích hình chóp & ví dụ minh họa. Bài viết này sẽ là nguồn thông tin hữu ích cho bạn.

I. Hình chóp là gì? Hình chóp đều là gì?

1. Định nghĩa về hình chóp

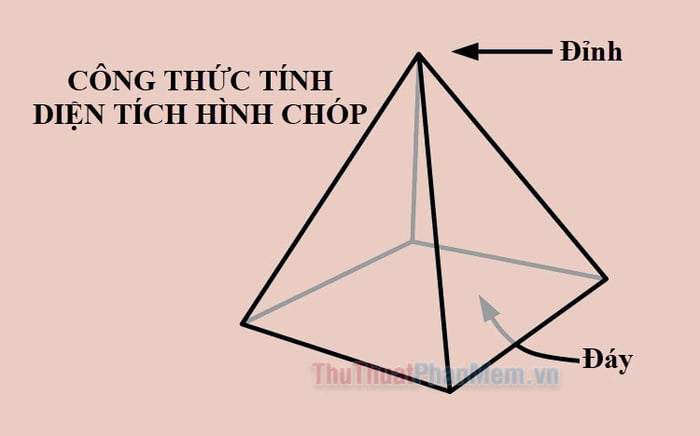
Hình chóp trong không gian là hình đa diện, đáy là đa giác lồi, mặt bên hình tam giác, và đỉnh là điểm không nằm trên đáy.

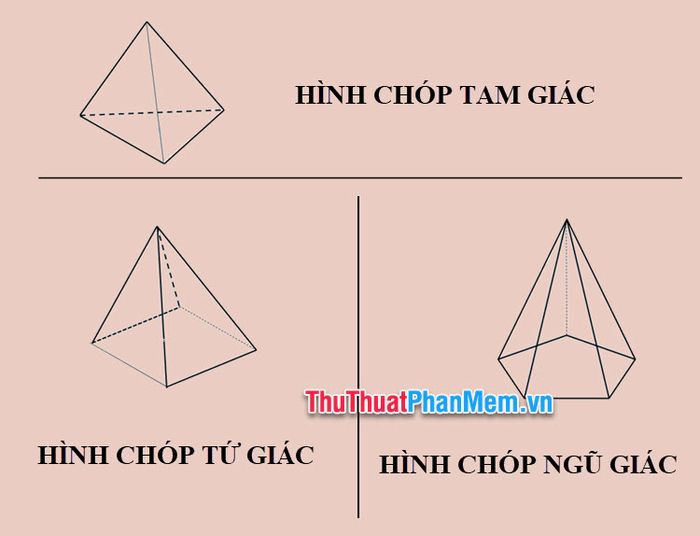
Có nhiều loại hình chóp khác nhau, được đặt tên theo hình đáy. Ví dụ: Hình chóp tam giác đều có đáy là tam giác đều, hình chóp tam giác có đáy là tam giác, hình chóp tứ giác có đáy là tứ giác, hình chóp thang có đáy là hình thang, hình chóp bình hành có đáy là hình bình hành,...

2. Đặc điểm của hình chóp

Đường cao của hình chóp là đường thẳng đi qua đỉnh và vuông góc với mặt đáy
Nếu các cạnh bên hoặc các góc ở đỉnh bằng nhau, hoặc các cạnh bên bằng nhau, thì đường cao chính là tâm đường tròn ngoại tiếp đáy
Nếu mặt bên hoặc mặt chéo vuông góc với mặt đáy, đường cao của hình chóp sẽ là đường cao của mặt đó
Nếu các mặt bên hợp với mặt đáy ở các góc bằng nhau, hoặc các đường cao xuất phát từ đỉnh đều trùng nhau, thì chân đường cao là tâm đường tròn nội tiếp mặt đáy

3. Hình chóp đều là gì?

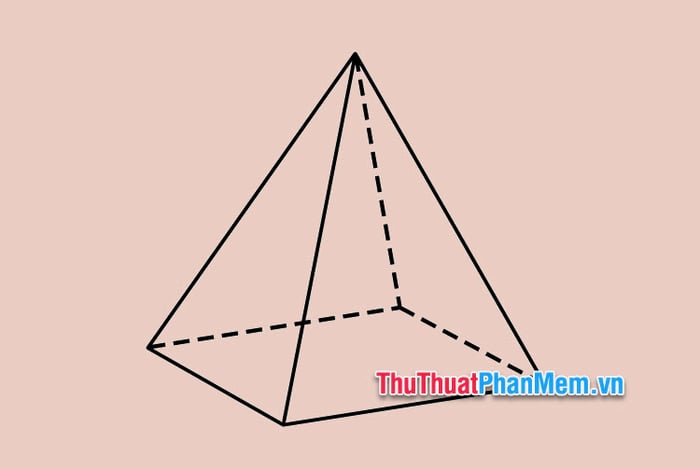
Hình chóp đều trong không gian là một dạng đặc biệt, đáy là đa giác đều với các tam giác bên bằng nhau. Ví dụ: Hình chóp tam giác đều, hình chóp tứ giác đều,...

Đặc điểm của hình chóp đều:

Đáy là đa giác đều như hình vuông, tam giác đều, ngũ giác đều,...
Tâm của đa giác đáy trùng với chân đường cao của hình chóp đều

II. Công thức tính diện tích hình chóp

1. Công thức tính diện tích xung quanh hình chóp

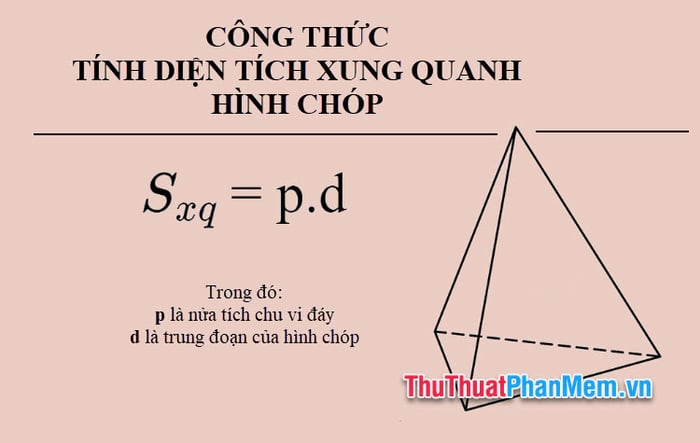
Diện tích xung quanh của hình chóp là tổng diện tích các mặt bên. Sử dụng công thức:

$S_{x q}$ = p.d

Trong công thức:

$S_{x q}$ là diện tích xung quanh của hình chóp
p là nửa tích chu vi đáy
d là trung điểm của hình chóp (đường cao vẽ từ đỉnh xuống trung điểm mỗi cạnh đa giác đáy là trung điểm của hình chóp đó)

Ghi chú: Công thức trên chỉ dành cho các hình chóp có các mặt bên là hình tam giác đều. Đối với hình chóp có các mặt bên khác nhau, cần tính diện tích từng mặt rồi cộng tổng để có diện tích xung quanh.

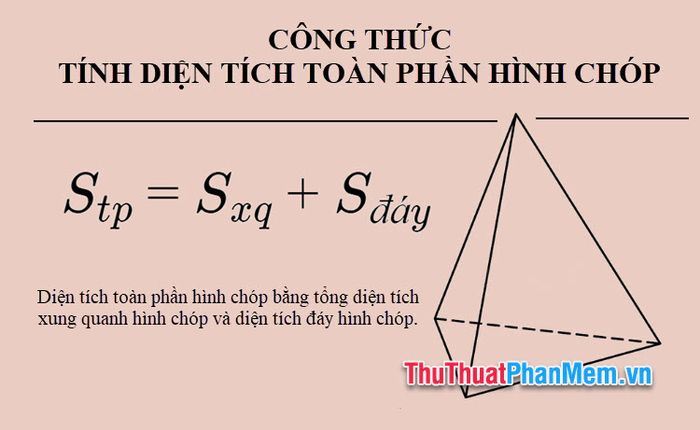
2. Công thức tính diện tích toàn phần hình chóp

Diện tích toàn phần của hình chóp là tổng diện tích xung quanh và diện tích đáy.

$S_{t p}$

S_{t p}

S_{x q}

S_{đ á y}

III. Ví dụ minh họa

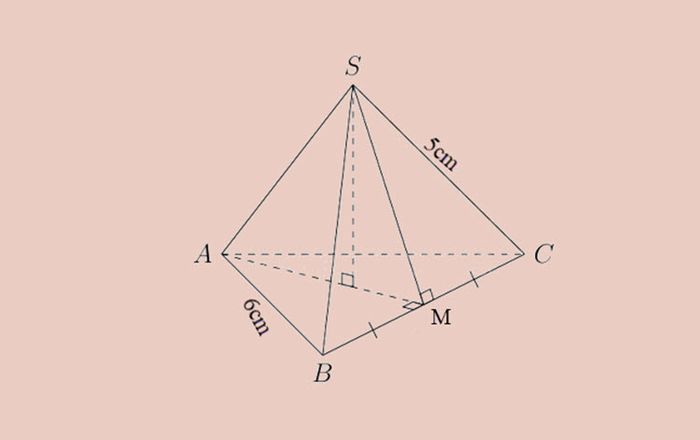
Ví dụ 1: Cho hình chóp tam giác đều, cạnh đáy dài 6 cm, các cạnh bên 5cm. Tính diện tích xung quanh và diện tích toàn phần.

Bài giải

- Hình chóp tam giác đều có đáy dài 6cm, với các cạnh bên là 5cm.

- Gọi hình chóp tam giác đều là S.ABC, vẽ đường thẳng từ đỉnh S đến trung điểm AC (đặt là M). Đây là trung đoạn d của hình chóp.

- Vì tam giác SBC là tam giác cân tại S, tam giác SBM là tam giác vuông tại M. Bản chất BM bằng 1 nửa BC và độ dài là 3 cm. Sử dụng định lý Pytago cho tam giác vuông SBM, ta có:

Kết quả là: SM2=SB2−BM2=52−32=16S_M^2 = S_B^2 - B_M^2 = 52 - 32 = 16SM2=SB2−BM2=52−32=16

=> SM=4SM = 4SM=4 cm (SM là trung đoạn d của hình chóp).

Áp dụng công thức tính diện tích xung quanh hình chóp, ta có:

Diện tích xung quanh Sxq=pcdotd=frac6times32cdot4=9.4=36cm2S_{xq} = p \cdot d = \frac{6 \times 3}{2} \cdot 4 = 9.4 = 36 \ cm^2Sxq=pcdotd=frac6times32cdot4=9.4=36cm2

Diện tích tam giác đáy là: Sđaˊy=a2timesfracsqrt34=62timesfracsqrt34=9sqrt3cm2S_{đáy} = a^2 \times \frac{\sqrt{3}}{4} = 62 \times \frac{\sqrt{3}}{4} = 9\sqrt{3} \ cm^2Sđaˊy=a2timesfracsqrt34=62timesfracsqrt34=9sqrt3cm2

Áp dụng công thức diện tích toàn phần hình chóp, ta có: Stp=Sxq+Sd=36+9sqrt3approx51.59cm2S_{tp} = S_{xq} + S_d = 36 + 9\sqrt{3} \approx 51.59 \ cm^2Stp=Sxq+Sd=36+9sqrt3approx51.59cm2

Ví dụ 2: Hình chóp tứ giác đều, chiều cao tam giác mỗi mặt bằng 10 cm, cạnh đáy là 20 cm. Diện tích toàn phần là bao nhiêu?

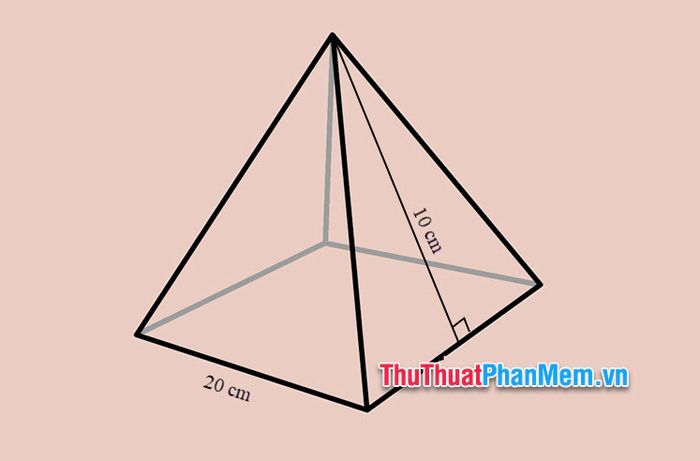
Ví dụ 2: Cho hình chóp tứ giác đều có chiều cao tam giác mỗi mặt bên bằng 10 cm, độ dài cạnh đáy bằng 20 cm. Tính diện tích toàn phần hình chóp tứ giác đều.

Bài toán giải quyết

Hình chóp tứ giác đều có các cạnh đáy bằng nhau, mỗi cạnh là 20 cm.

Diện tích mặt bên (tam giác) của hình chóp là:

S=frac12times10times20=100cm2S = \frac{1}{2} \times 10 \times 20 = 100 \ cm^2S=frac12times10times20=100cm2

Diện tích xung quanh của hình chóp là: Sxq=400cm2S_{xq} = 400 \ cm^2Sxq=400cm2

Áp dụng công thức diện tích toàn phần hình chóp, ta có: Stp=Sxq+Sa=400+20.20=800cm2S_{tp} = S_{xq} + S_a = 400 + 20.20 = 800 \ cm^2Stp=Sxq+Sa=400+20.20=800cm2

Áp dụng công thức tính diện tích toàn phần hình chóp, ta có:

$S_{t p} = S_{x q} + S_{a} = 400 + 20.20 = 800 {c m}^{2}$

Diện tích toàn phần của hình chóp là 800 cm².

Mytour hy vọng bạn sẽ áp dụng thành công công thức tính diện tích hình chóp trong các bài toán thực tế. Cảm ơn sự quan tâm và theo dõi bài viết!

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]

Các câu hỏi thường gặp

Hình chóp là gì và đặc điểm của nó như thế nào?

Hình chóp là một hình đa diện với đáy là một đa giác lồi và mặt bên là các hình tam giác. Đặc điểm nổi bật của hình chóp bao gồm đường cao vuông góc với mặt đáy, và tâm của đa giác đáy trùng với chân đường cao nếu đáy là đa giác đều.

Công thức tính diện tích xung quanh của hình chóp là gì?

Công thức tính diện tích xung quanh hình chóp là Sxq = p.d, trong đó p là nửa tích chu vi đáy, và d là chiều cao từ đỉnh đến trung điểm của các cạnh đáy. Công thức này chỉ áp dụng cho hình chóp có mặt bên là tam giác đều.

Cách tính diện tích toàn phần của hình chóp là gì?

Diện tích toàn phần của hình chóp được tính bằng công thức Stp = Sxq + Sđáy, trong đó Sxq là diện tích xung quanh và Sđáy là diện tích của đáy. Việc tính toán này giúp tổng hợp tất cả diện tích của hình chóp.

Hình chóp tứ giác đều có diện tích toàn phần là bao nhiêu?

Diện tích toàn phần của hình chóp tứ giác đều được tính bằng công thức Stp = Sxq + Sa. Ví dụ, nếu diện tích xung quanh là 400 cm² và diện tích đáy là 20 x 20, thì tổng diện tích toàn phần là 800 cm².

Có nhiều loại hình chóp khác nhau không?

Có, hình chóp được phân loại dựa trên hình dáng của đáy, chẳng hạn như hình chóp tam giác, hình chóp tứ giác, và hình chóp thang. Mỗi loại hình chóp có những đặc điểm riêng biệt về cấu trúc và công thức tính diện tích.