Bí quyết Tính Thể tích

Thể tích của một hình là khối lượng không gian mà hình đó chiếm trong không gian ba chiều. Bạn có thể hiểu thể tích như lượng nước (hoặc không khí, hoặc cát, v.v.) mà hình đó có thể chứa khi được đổ đầy. Đơn vị phổ biến của thể tích bao gồm cm³, m³, in³, và ft³. Hướng dẫn này sẽ chỉ cho bạn cách tính thể tích của 6 hình khối thường gặp trong toán học, bao gồm hình lập phương, hình hộp chữ nhật, hình trụ, hình chóp, hình nón và hình cầu. Bạn có thể nhận ra rằng các công thức tính thể tích có nhiều điểm tương đồng và có thể ghi nhớ dễ dàng từ đó. Hãy theo dõi các bước sau để kiểm tra xem bạn đã hiểu các điểm đó chưa!

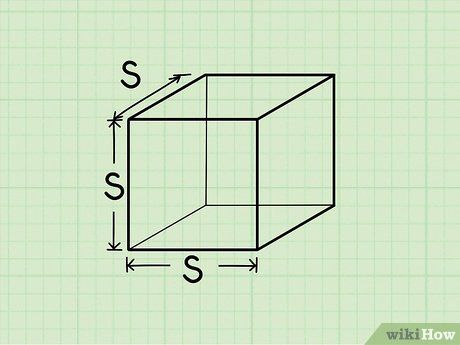
Nhận biết hình lập phương. Hình lập phương là một hình khối ba chiều có 6 mặt là hình vuông. Nói cách khác, đây là một hình hộp mà tất cả các cạnh đều bằng nhau. Ví dụ như viên xúc xắc 6 mặt hoặc khối đường nén là các ví dụ về hình lập phương phổ biến mà bạn có thể gặp hàng ngày.

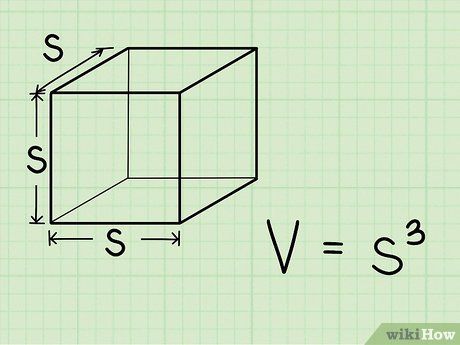
Bí quyết Tính Thể tích Hình lập phương.

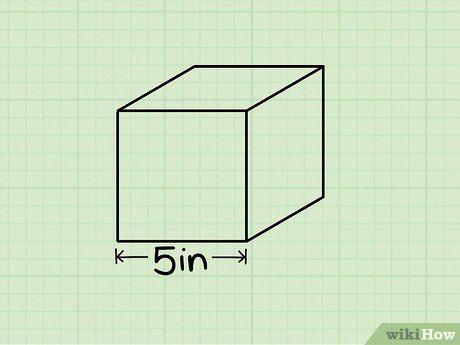
Bước 1: Xác định cạnh của hình lập phương. Nếu cạnh của hình lập phương được cho sẵn, bạn đã có một bước nhanh chóng vào việc tính toán. Nếu không, hãy sử dụng thước kẻ để đo cạnh của nó.

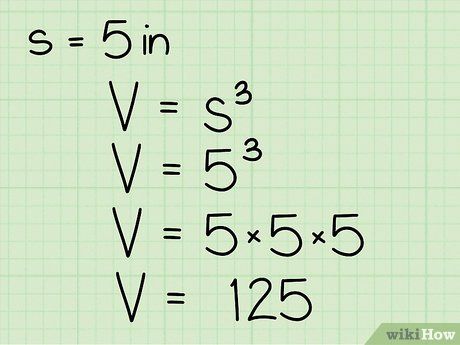
Bước 2: Thay chiều dài cạnh vào công thức thể tích. Với ví dụ, nếu cạnh của hình lập phương là 5 inches, thì thể tích sẽ là 125 in³.

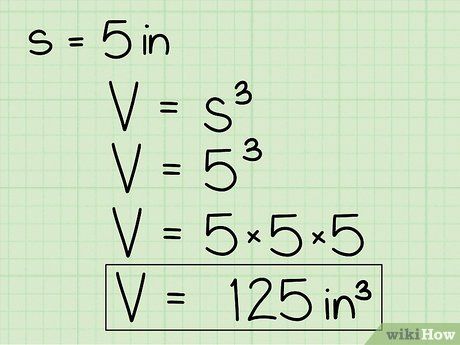
Bước 3: Ghi kết quả với đơn vị khối. Trong ví dụ này, nếu cạnh của hình lập phương là inch, kết quả sẽ là 125 inch khối.

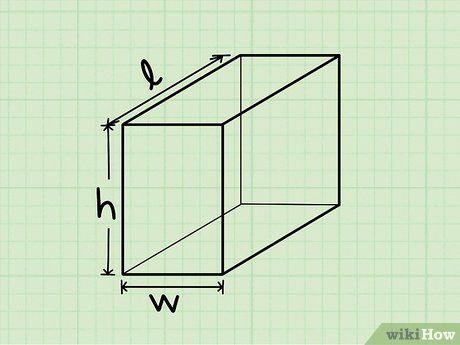
Bí quyết Tính Thể tích Hình hộp chữ nhật.

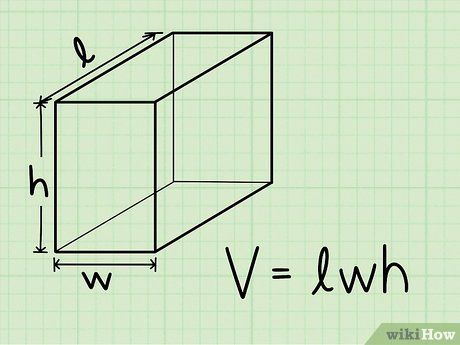
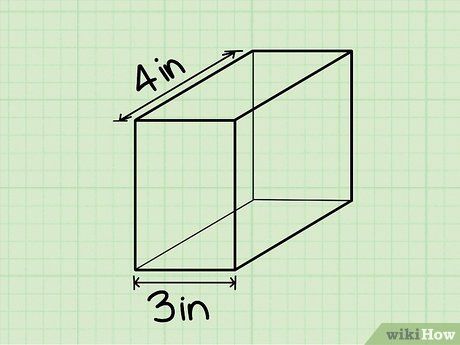
Bước 1: Xác định chiều dài, chiều rộng và chiều cao. Lấy các giá trị đo được từ biểu đồ hoặc bằng cách sử dụng thước.

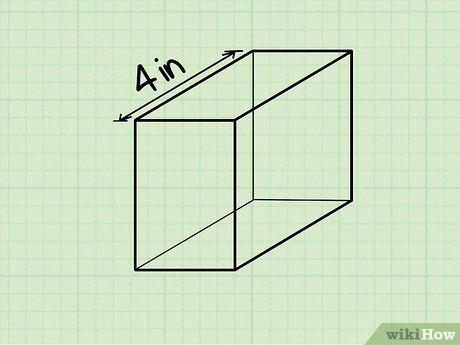
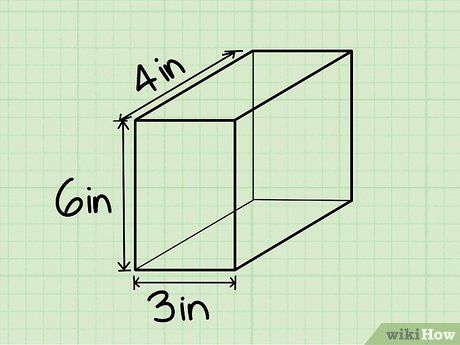
Bước 2: Thay các giá trị vào công thức tính thể tích. Ví dụ, nếu chiều dài, chiều rộng và chiều cao lần lượt là 4, 3 và 6 inches, thì thể tích sẽ là 72 in³.

Bước 3: Ghi kết quả với đơn vị khối. Trong ví dụ này, nếu các cạnh được đo bằng inch, kết quả sẽ là 72 inch khối.

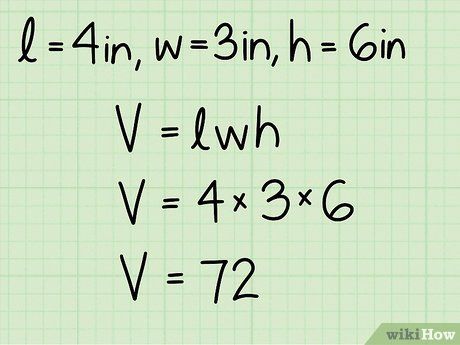
Thay các giá trị đã xác định vào công thức tính thể tích hình trụ tròn: V = πr²h. Từ các ví dụ trên, ta có: r = 4 in, h = 6 in. Vậy, V = 3.14 * 4² * 6, hay 301.44.

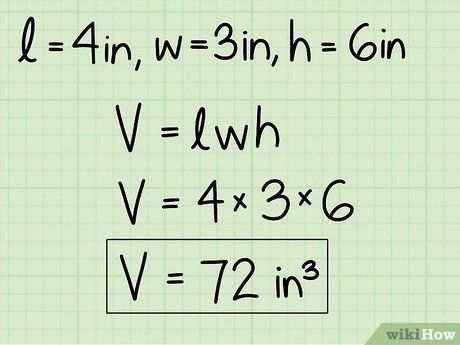
Đảm bảo kết quả được ghi theo đơn vị khối (mũ 3 của đơn vị đo). Ví dụ: Nếu chiều cao và bán kính của hình trụ tròn lần lượt là: r = 2 cm, h = 4 cm, thì thể tích sẽ là: 3.14 * 2² * 4, hoặc 50.24 cm³.

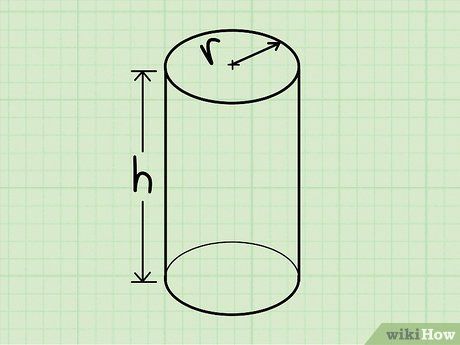
Biết ngay hình trụ. Hình trụ là một dạng hình khối không gian có 2 đáy hình tròn giống nhau và một mặt dạng hình vòng cung kết nối hai đáy đó.

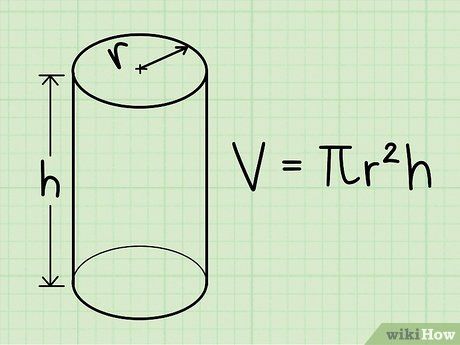
Công thức tính thể tích hình trụ tròn. Thể tích = πr²h, với r là bán kính đáy, h là chiều cao, và π là hằng số pi. Trong phần lớn trường hợp, giá trị của π được làm tròn thành 3.14. Ví dụ, nếu r = 5 cm và h = 8 cm, thì thể tích sẽ là 3.14 * 5² * 8, hoặc 628 cm³.

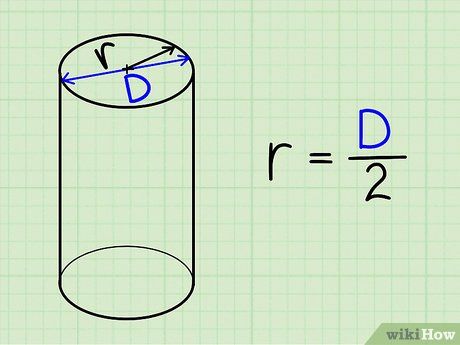
Xác định bán kính của mặt đáy. Ví dụ: Nếu đường kính của mặt đáy là 6 cm, bán kính sẽ là 3 cm.

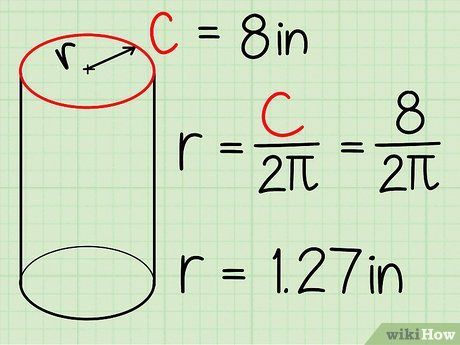
Đo và tính bán kính mặt đáy. Ví dụ: Nếu chu vi mặt đáy là 12 inches, bán kính sẽ là 1.91 inches.

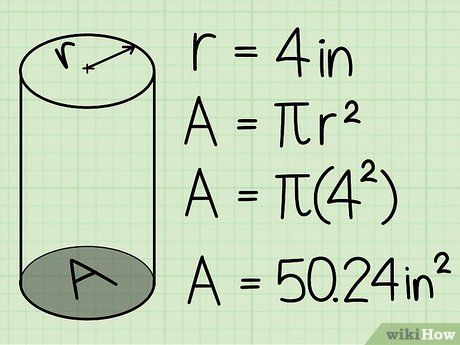
Tính diện tích mặt đáy của hình trụ tròn. Ví dụ: Nếu bán kính mặt đáy là 5 cm, diện tích mặt đáy sẽ là 78.5 cm².

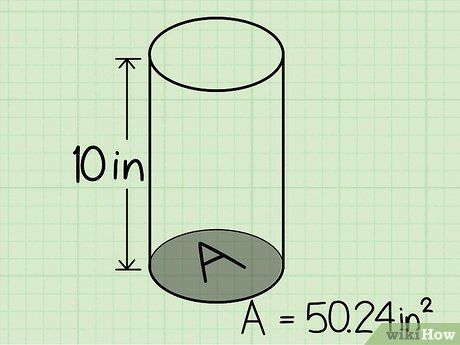
Xác định chiều cao của hình trụ tròn. Hãy đo chiều cao bằng thước kẻ hoặc xem trên giản đồ.

Tính thể tích của hình trụ tròn. Ví dụ: Nếu bán kính mặt đáy là 4 cm và chiều cao là 10 cm, thể tích sẽ là 502.4 cm³.

Kết quả tính thể tích cần được biểu thị bằng khối (mũ 3 của đơn vị đo). Ví dụ: Nếu hình chóp có đáy là hình vuông được đo bằng inches và có diện tích là 36 in², thì thể tích sẽ là 72 in³.

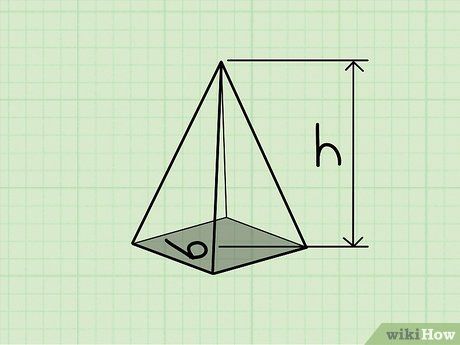
Tính diện tích mặt đáy của hình chóp. Ví dụ: Nếu mặt đáy là hình vuông với cạnh là 6 inches, diện tích mặt đáy sẽ là 36 in².

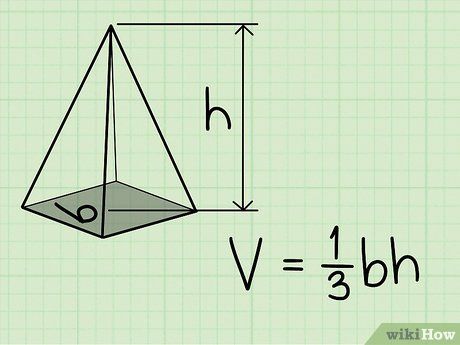
Tính thể tích của hình chóp đa giác đều. Ví dụ: Nếu diện tích mặt đáy là 36 in² và chiều cao là 10 inches, thể tích sẽ là 120 in³.

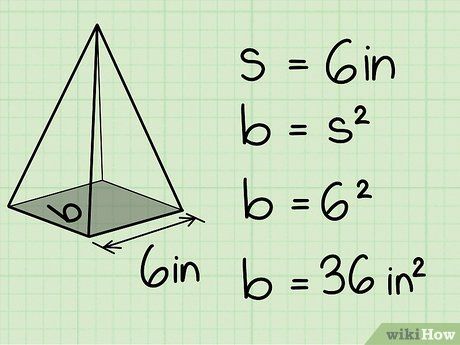
Tính diện tích mặt đáy của hình chóp. Ví dụ: Nếu mặt đáy là hình vuông với cạnh là 6 inches, diện tích mặt đáy sẽ là 36 in².

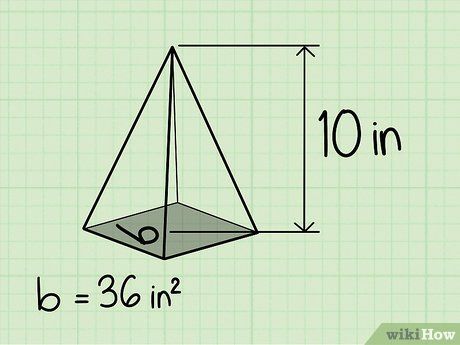
Chiều cao của hình chóp là 10 inches.

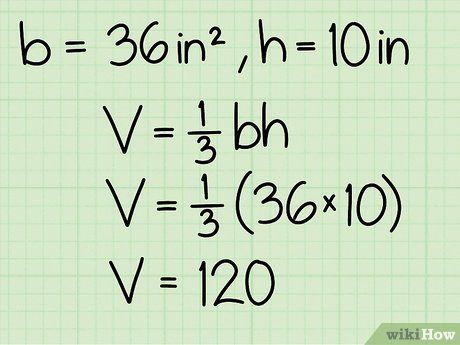
Thể tích của hình chóp là 120 inches khối.

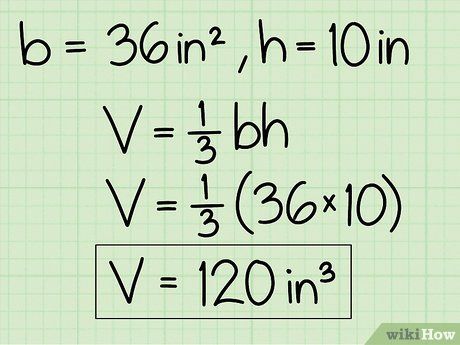
Thể tích của hình chóp là 120 inches khối.

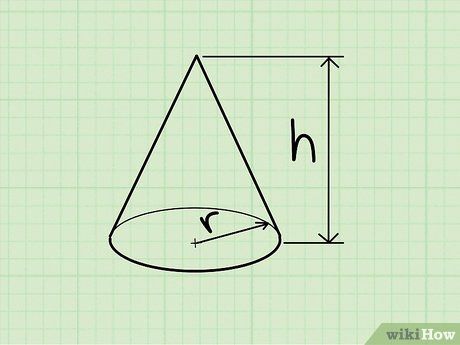
Thể tích của hình nón được tính bằng công thức: V=1/3πr²h, với r là bán kính đáy và h là chiều cao.

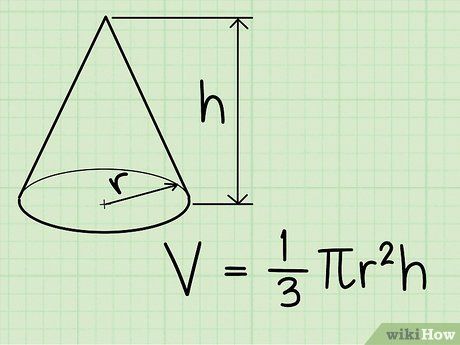
Thể tích của hình nón là 1/3πr²h.

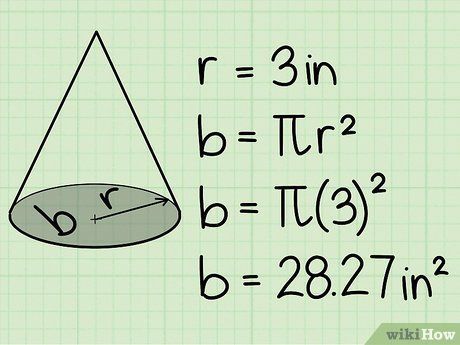
Diện tích mặt đáy của hình nón là 28.27 in².

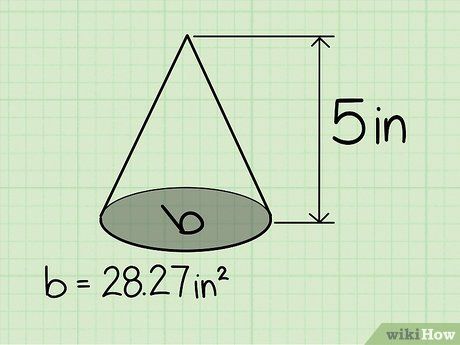
Chiều cao của hình nón là 5 inches.

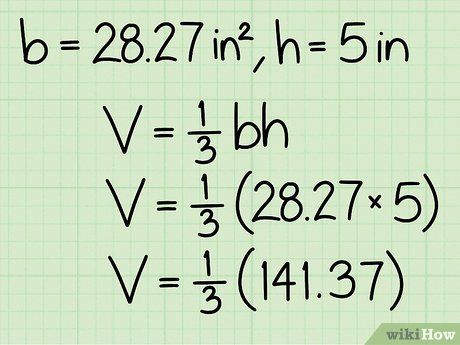
Thể tích của hình nón là 47.12 inches khối.

Thể tích của hình nón là 47.12 inches khối.

Thể tích của hình cầu là 47.12 in³.

Thể tích của hình cầu là 47.12 in³.

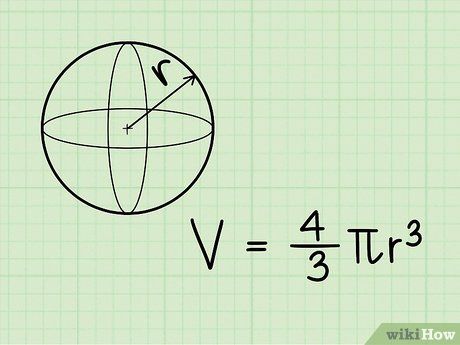
Thể tích của hình cầu là 47.12 in³.

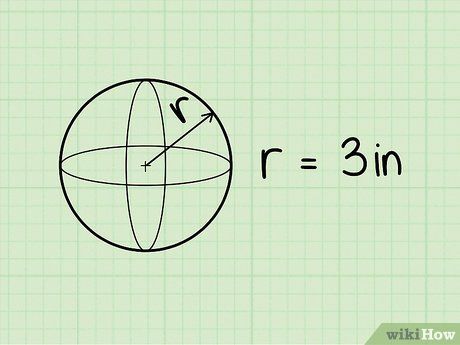
Thể tích của hình cầu là 47.12 in³.

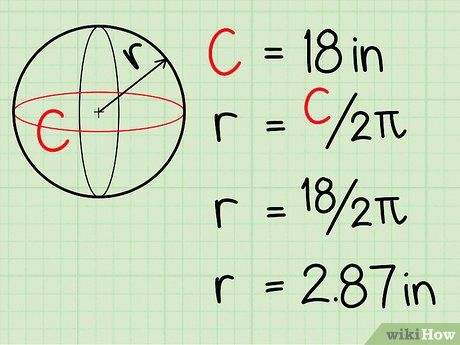
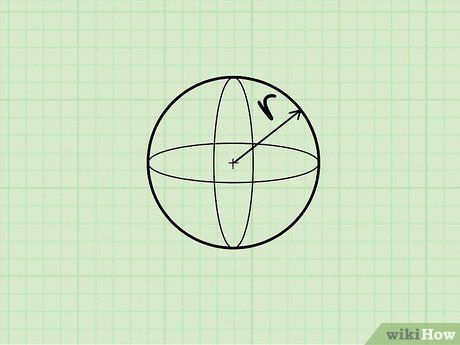
Bán kính của hình cầu là 2.87 in.

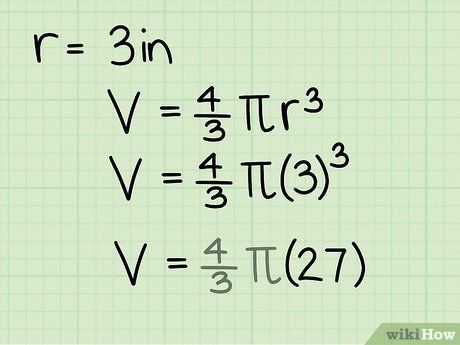
Bán kính của hình cầu là 2.87 in.

Thể tích của hình cầu là 36 inch khối (36 in³).

Thể tích của hình cầu là 113.04 inch khối (113.04 in³).

Thể tích của hình cầu là 113.04 inch khối (113.04 in³).