Biểu đồ của hàm số

Biểu đồ của hàm số f trong toán học là tập hợp tất cả các cặp có thứ tự (x, f(x)). Nếu đầu vào x là một cặp có thứ tự các số thực (x₁, x₂) thì biểu đồ của hàm số f là tập hợp tất cả các bộ ba có thứ tự (x₁, x₂, f(x₁, x₂)), và đối với một hàm liên tục thì đó là một mặt.

Nói một cách đơn giản, nếu x là một số thực và f là một hàm số thực thì biểu đồ là sự biểu diễn trực quan sinh động của tập hợp này trong hệ tọa độ Descartes.

Có thể tổng quát hóa biểu đồ hàm số về mặt đồ thị của một tương đối. Ghi chú rằng mặc dù hàm số luôn liên kết với biểu đồ của nó nhưng hàm số và biểu đồ không đồng nhất với nhau, bởi vì có trường hợp hai hàm số có tập giá trị (codomain) khác nhau nhưng biểu đồ vẫn như nhau.

Do hệ tọa độ Descartes được sử dụng để biểu diễn các chiều không gian (biểu thị), tối đa có 3 chiều kích thước, nên hệ tọa độ Descartes cũng chỉ biểu diễn được biểu đồ hàm số một biến và biểu đồ hàm số 2 biến mà thôi.

Trong các lĩnh vực như khoa học, công nghệ, tài chính và nhiều lĩnh vực khác, đồ thị hàm số được sử dụng rất phổ biến, thường dùng hệ tọa độ Descartes.

Biểu đồ hàm số một biến

Đồ thị của hàm số một biến là biểu đồ của hàm số y = f(x) là tập hợp các điểm trên mặt phẳng R2 có tọa độ [x, f(x)]. Đồ thị của hàm số

$f\left(x\right)=\{\begin{array}{cc}a,& \text{nếu }x=1\\ \end{array}$

d , nếu  x = 2 c , nếu  x = 3. {\displaystyle f(x)=\left\{{\begin{matrix}a,&{\mbox{nếu }}x=1\\d,&{\mbox{nếu }}x=2\\c,&{\mbox{nếu }}x=3.\end{matrix}}\right.}

là

{(1,a), (2,d), (3,c)}.

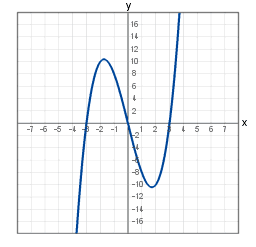
Đồ thị của đa thức bậc ba trên đường thẳng số thực

$f\left(x\right)=x^3-<!--\; -\; -->9x$

là

{(x, x − 9x): x là một số thực}

Nếu vẽ tập này trên mặt phẳng, sẽ thu được một đường cong (xem hình minh hoạ).

Hàm hai biến

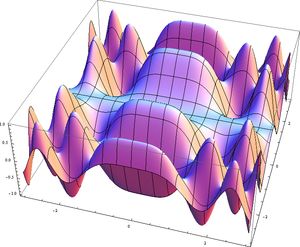
Đồ thị của hàm số lượng giác trên đường thẳng số thực

f(x, y) = sin(x) · cos(y)

là

{(x, y, sin(x) · cos(y)): x và y là hai số thực}.

Nếu biểu diễn tập này trên hệ tọa độ Decartes, ta sẽ thu được một mặt (xem hình minh hoạ).

Đường tiếp tuyến của đồ thị

Giả sử hàm số f có n biến số: $x=x_1,\dots <!--\; \dots \; -->,x_n$, đường tiếp tuyến của đồ thị là

$(\mathrm{\nabla <!--\; \nabla \; -->}f,-<!--\; -\; -->1)$

Phương pháp kiểm nghiệm

Để kiểm tra xem một đường có phải là đồ thị của hàm số theo biến x hay không, ta sử dụng phương pháp kiểm nghiệm đường dọc; tương tự, để kiểm tra xem nó có phải là đồ thị của hàm số theo biến y hay không, ta sử dụng phương pháp kiểm nghiệm đường ngang. Nếu hàm số có hàm nghịch đảo, ta có thể xác định đồ thị của hàm nghịch đảo bằng cách vẽ đối xứng của đồ thị gốc qua trục đối xứng là đường y = x.

Tổng quát hóa

Đồ thị của một hàm số được lưu trong một tích của các tập hợp Descartes. Mặt phẳng X-Y là tích Descartes của hai đường thẳng X và Y, trong khi hình trụ là tích Descartes của một đường thẳng và một đường tròn (có chiều cao, bán kính và góc xác định chính xác vị trí các điểm).

Liên kết bên ngoài.

• Bộ dụng cụ vẽ đồ thị hàm số, đạo hàm và nguyên hàm Lưu trữ 2016-03-18 tại Wayback Machine
• Weisstein, Eric W. 'Đồ thị hàm số.' Từ MathWorld—Tài nguyên trang web của Wolfram.