Biểu đồ tương quan là gì? Tính chất và chức năng của biểu đồ này

1. Định nghĩa biểu đồ tương quan

Biểu đồ tương quan (biểu đồ phân tán) là cách thể hiện các cặp giá trị của biến độc lập và biến phụ thuộc qua hình ảnh. Để các số liệu có ý nghĩa, cần phải vẽ một đường phù hợp qua các điểm thể hiện mối quan hệ giữa hai biến. Biểu đồ này hữu ích khi một biến liên tục được kiểm soát và biến còn lại phụ thuộc vào nó, hoặc khi cả hai biến đều độc lập. Tham số thay đổi được vẽ trên trục hoành, còn biến phụ thuộc vẽ trên trục tung. Nếu không có biến phụ thuộc, một trong hai biến có thể được vẽ trên bất kỳ trục nào và độ phân tán sẽ chỉ cho thấy mức độ tương quan giữa chúng.

Biểu đồ tương quan được vẽ bằng các điểm trên mặt phẳng tọa độ, với trục hoành đại diện cho biến độc lập (nguyên nhân) và trục tung cho biến phụ thuộc (kết quả). Biểu đồ này giúp nhận diện mức độ và hướng của sự tương quan giữa hai biến. Nếu các điểm gần một đường thẳng, hai biến có tương quan tuyến tính. Nếu đường thẳng có dốc dương, hai biến có tương quan dương, nghĩa là khi biến độc lập tăng thì biến phụ thuộc cũng tăng. Ngược lại, nếu dốc âm, hai biến có tương quan âm. Nếu các điểm không gần đường thẳng nào, hai biến có thể không có tương quan hoặc có tương quan phi tuyến.

Biểu đồ tương quan, còn được gọi là biểu đồ phân tán hoặc Scatter diagram, là một loại biểu đồ dùng để thể hiện mối liên hệ giữa các yếu tố ảnh hưởng đến chất lượng. Biểu đồ này được tạo ra bằng các điểm trên hệ tọa độ, giúp xác định các mối quan hệ giữa hai biến hoặc giữa hai bộ dữ liệu trên đồ thị.

- Trục X biểu diễn biến được dự đoán - Biến phụ thuộc

- Trục Y đại diện cho biến dùng để dự đoán - Biến độc lập

Khi đã xác định được mối liên hệ giữa các biến, bạn có thể dự đoán giá trị của biến phụ thuộc dựa trên số liệu của biến độc lập.

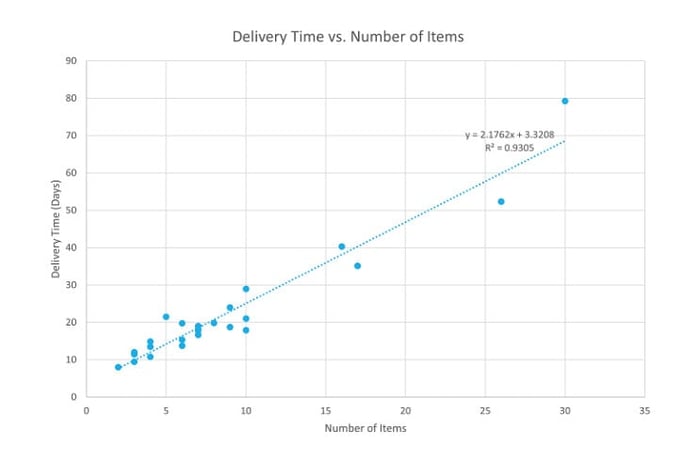
Biểu đồ phân tán là dạng biểu đồ sử dụng các điểm để biểu thị mối liên hệ giữa hai biến định lượng. Nó giúp phân tích các mẫu hình, tuyến tính, độ dốc và mức độ tập trung của dữ liệu. Dưới đây là một số ví dụ về biểu đồ phân tán:

- Biểu đồ phân tán thể hiện mối quan hệ giữa nhiệt độ và tốc độ làm đông nước đá. Biểu đồ này cho thấy mối liên hệ nghịch biến, tức là khi nhiệt độ tăng thì tốc độ làm đông giảm và ngược lại. Mối quan hệ này khá mạnh vì các điểm gần gũi với một đường thẳng.

- Biểu đồ phân tán về mối liên hệ giữa chiều cao và cân nặng của một nhóm người. Biểu đồ cho thấy mối quan hệ thuận biến, nghĩa là khi chiều cao tăng thì cân nặng cũng tăng. Mối quan hệ này yếu vì các điểm phân tán không theo một hướng rõ ràng.

- Biểu đồ phân tán về mối quan hệ giữa số lượng bài viết trên blog và số lượt xem. Biểu đồ cho thấy không có mối liên hệ rõ ràng, vì các điểm phân tán không có hình mẫu hay xu hướng cụ thể. Số lượt xem có thể bị ảnh hưởng bởi các yếu tố khác như chất lượng bài viết, chủ đề, thời gian, v.v…

2. Tính chất của biểu đồ tương quan

- Một chỉ tiêu chất lượng được hình thành nhờ sự kết hợp và ảnh hưởng của nhiều yếu tố khác nhau. Mối quan hệ giữa chất lượng và các yếu tố này là rất chặt chẽ.

- Để đánh giá tình trạng chất lượng, người ta có thể sử dụng hai hoặc nhiều dữ liệu cùng lúc để thể hiện mối tương quan giữa các yếu tố trên đồ thị.

- Thông qua biểu đồ, có thể xác định xu hướng tác động của nguyên nhân đang được xem xét đến kết quả đạt được.

- Biểu đồ này thể hiện mối quan hệ giữa hai biến định lượng bằng cách sử dụng các điểm trên hệ tọa độ. Nó giúp nhận diện các mẫu hình, độ dốc và mức độ tập trung của dữ liệu. Nó cũng có thể dự đoán kết quả của biến phụ thuộc dựa trên biến độc lập nếu có một mối liên hệ rõ ràng.

- Để đảm bảo tính chính xác của mối quan hệ giữa hai biến, cần có một lượng dữ liệu đủ lớn và đại diện cho toàn bộ phạm vi quan sát. Biểu đồ không thể xác định nguyên nhân và kết quả, chỉ có thể cho biết sự tương quan thống kê giữa chúng.

Trước khi bắt đầu phân tích tương quan hoặc hồi quy, bạn nên kiểm tra dữ liệu bằng biểu đồ tương quan. Biểu đồ này cung cấp cái nhìn hữu ích về mối quan hệ tuyến tính giữa hai biến và giúp phát hiện các điểm bất thường. Ngoài ra, biểu đồ cũng cung cấp cái nhìn ban đầu về mối quan hệ giữa hai biến. Ví dụ, bạn có thể sử dụng biểu đồ phân tán để kiểm tra mối quan hệ giữa chi phí quảng cáo và doanh số sản phẩm, xem có xu hướng tăng giảm doanh số khi chi phí quảng cáo thay đổi và ảnh hưởng của chi phí quảng cáo đến doanh số là bao nhiêu. Tương tự, bạn có thể khảo sát mối quan hệ giữa nhiệt độ và lượng CO2 trong không khí hoặc so sánh hiệu suất làm việc của các nhân viên trong công ty để đánh giá sự khác biệt về hiệu suất.

3. Mục đích và ý nghĩa áp dụng

3.1 Mục đích

Biểu đồ tương quan được dùng để phân tích các vấn đề và xác định điều kiện tối ưu thông qua việc đánh giá định lượng mối quan hệ nhân quả giữa hai yếu tố. Biểu đồ này giúp bạn xác định mức độ tương quan giữa hai biến số.

- Xác định mức độ tương quan giữa hai biến số

- Xác định sự tồn tại mối quan hệ giữa hai đặc tính bằng cách vẽ các cặp số liệu trên hệ tọa độ Oxy hoặc đặt một đặc tính trên trục Oy và đặc tính còn lại trên trục Ox.

- Khi xác định mối quan hệ giữa hai đặc tính, nếu một đặc tính tăng thì đặc tính kia cũng tăng, chứng tỏ chúng có mối quan hệ thuận và các điểm dữ liệu sẽ nằm trong vùng elip nghiêng về phía bên phải. Ngược lại, nếu một đặc tính giảm còn đặc tính kia tăng, chúng có mối quan hệ nghịch với các điểm dữ liệu nằm trong vùng elip nghiêng về phía bên trái.

- Nếu hai đặc tính không có mối quan hệ, các điểm dữ liệu sẽ phân tán thành hình tròn. Mối quan hệ giữa các đặc tính được thể hiện qua hệ số hồi quy hoặc hệ số tương quan r. Nếu giá trị gần -1 (<0,85), có mối quan hệ nghịch rất lớn (nghịch chặt). Nếu giá trị gần +1 (>0,85), có mối quan hệ thuận rất lớn (thuận chặt). Nếu giá trị gần 0, mối quan hệ giữa hai đặc tính rất kém. Dựa trên phân tích biểu đồ tương quan, hệ số tương quan r và phương trình hồi quy, có thể dự đoán chất lượng đặc tính và quá trình, cũng như xác định các yếu tố cần kiểm soát để đảm bảo chất lượng sản phẩm.

3.2 Vai trò và ý nghĩa

Việc phân tích và sử dụng dữ liệu chỉ dựa vào bảng biểu thường thiếu chính xác và không bao quát. Biểu đồ tương quan giúp thể hiện rõ ràng mối quan hệ giữa hai biến số, điều mà bảng biểu khó thể hiện được. Nhờ có biểu đồ tương quan, chúng ta có thể nhìn nhận mối liên hệ giữa các biến số một cách trực quan hơn.

- Nó giúp bạn nhận diện hướng và mức độ liên hệ giữa hai biến định lượng. Nếu đường xu hướng có độ dốc dương, điều này cho thấy hai biến có mối tương quan thuận, tức là khi một biến gia tăng, biến kia cũng tăng theo và ngược lại. Nếu đường xu hướng có độ dốc âm, nghĩa là hai biến có mối tương quan nghịch, tức là khi một biến tăng thì biến kia giảm và ngược lại. Nếu đường xu hướng gần như ngang hoặc không rõ ràng, điều đó cho thấy hai biến không có hoặc có mối tương quan rất yếu.

- Giúp bạn dự đoán giá trị của biến phụ thuộc từ giá trị của biến độc lập. Bạn có thể áp dụng công thức của đường xu hướng để tính giá trị dự đoán của biến phụ thuộc khi đã biết giá trị của biến độc lập. Ví dụ: với công thức đường xu hướng y = 2x + 5, khi x = 10, giá trị của y sẽ là 25.

- Nó hỗ trợ bạn kiểm tra mức độ phù hợp của mô hình hồi quy với dữ liệu. Bạn có thể so sánh các điểm phân tán với đường xu hướng để xác định sự gần gũi của chúng. Nếu các điểm phân tán gần với đường xu hướng, mô hình hồi quy khớp với dữ liệu và giải thích được phần lớn biến thiên. Ngược lại, nếu các điểm phân tán xa khỏi đường xu hướng, mô hình hồi quy không khớp với dữ liệu và không giải thích được nhiều biến thiên.

- Bạn có thể phát hiện và đánh giá các mối quan hệ giữa hai biến định lượng, có thể là quan hệ nguyên nhân - kết quả hoặc tương tác lẫn nhau. Nó giúp dự đoán kết quả của một biến dựa trên giá trị của biến khác, có thể nhằm tối ưu hóa hoặc kiểm soát một quá trình nào đó. Hơn nữa, bạn có thể kiểm tra sự phù hợp của mô hình hồi quy với dữ liệu để xác nhận hoặc bác bỏ một giả thuyết.

4. Quy trình lập biểu đồ tương quan

Để tạo biểu đồ tương quan trên Excel, bạn có thể thực hiện các bước sau để hoàn thiện biểu đồ của mình.

Bước 1: Chuẩn bị dữ liệu cho biểu đồ. Bạn cần có một bảng dữ liệu với hai cột: một cột cho biến độc lập và một cột cho biến phụ thuộc. Các giá trị của hai biến này phải là số liên tục. Ví dụ, bạn có thể có bảng dữ liệu về chi phí quảng cáo và doanh số bán hàng của một sản phẩm.

Bước 2: Lựa chọn dữ liệu cho biểu đồ. Bạn có thể chọn toàn bộ bảng dữ liệu hoặc chỉ hai cột chứa giá trị của các biến. Sau đó, vào tab Insert > biểu đồ phân tán > và chọn loại biểu đồ phân tán bạn muốn, chẳng hạn như biểu đồ phân tán với các điểm tròn.

Bước 3: Thêm đường xu hướng vào biểu đồ. Đường xu hướng giúp thể hiện xu hướng của dữ liệu thông qua các điểm phân tán. Để thêm đường xu hướng, nhấp chuột phải vào một điểm trên biểu đồ, chọn Add Trendline và chọn loại đường xu hướng bạn muốn trong hộp thoại Format Trendline2, chẳng hạn như đường xu hướng tuyến tính.

Bước 4: Tùy chỉnh biểu đồ theo ý thích của bạn. Bạn có thể thay đổi tên biểu đồ, tên các trục, nhãn dữ liệu, chú thích, màu sắc và kiểu nét vẽ để làm cho biểu đồ trở nên rõ ràng và sinh động hơn. Sử dụng các công cụ trong tab Design và Format để thực hiện các chỉnh sửa, ví dụ như thay đổi tên biểu đồ thành 'Mối quan hệ giữa chi phí quảng cáo và doanh số bán hàng'.

Khi các hệ số đã được vẽ trên đồ thị, bạn cần tiến hành so sánh hai biến số dựa trên sự tương quan của chúng. Các mối tương quan này được thể hiện như sau:

- Tương quan dương: Là mối quan hệ mà sự gia tăng của biến số nguyên nhân dẫn đến sự gia tăng của biến số kết quả.

- Tương quan âm: Là mối quan hệ mà sự gia tăng của biến số nguyên nhân dẫn đến sự giảm sút của biến số kết quả.

- Không có tương quan: Hai biến số không có mối liên hệ nào với nhau. Tình trạng này chỉ ra rằng có thể có vấn đề chất lượng từ các nguyên nhân khác.