1. Tổng hợp kiến thức môn Toán lớp 6 học kỳ 1 - Phần số học
1.1. Tập hợp và các phần tử của tập hợp
Tập hợp là khái niệm cơ bản trong toán học và đời sống, cho phép nhóm các đối tượng theo một tiêu chí chung. Ký hiệu a thuộc tập hợp A được biểu thị bằng a ∈ A, trong khi ký hiệu b không thuộc tập hợp A được viết là b ∉ A.
Lưu ý: Tập hợp các số tự nhiên được ký hiệu là N (bao gồm số 0), trong khi tập hợp các số tự nhiên khác 0 được ký hiệu là N*.
Các ví dụ về tập hợp:
- Tập hợp A bao gồm các môn học: A = {Toán, Lý, Hóa, Sinh, Anh văn}.
- Tập hợp B chứa các số chẵn từ 1 đến 10: B = {2, 4, 6, 8, 10}.
- Tập hợp C gồm các sinh viên trong lớp: C = {Thảo, Nguyên, Hương, Quỳnh, Tươi, Toàn, Thúy, Thăng}
1.2. Số lượng phần tử trong một tập hợp và các tập hợp con
Một tập hợp có thể chứa một hoặc nhiều phần tử, hoặc thậm chí không chứa phần tử nào. Theo đó:
- Tập hợp rỗng là tập hợp không chứa bất kỳ phần tử nào. Nó thường được ký hiệu bằng ø hoặc {}.
- Tập hợp con A của tập hợp B là tập hợp mà mọi phần tử của A đều nằm trong B. Để biểu thị điều này, ta sử dụng ký hiệu A ⊂ B. Ký hiệu A ⊆ B có nghĩa là A là tập hợp con của B hoặc bằng B, tức là A có thể bằng B hoặc chỉ là một phần của B.
Ví dụ: Tập hợp A = {1, 2} là tập hợp con của B = {1, 2, 3}, vì tất cả các phần tử của A đều thuộc B. Do đó, ta có A ⊂ B.
1.3. Phép cộng và phép nhân
- Tính chất giao hoán:
- Trong phép cộng: Đổi chỗ các số hạng trong một tổng không làm thay đổi tổng đó. Ví dụ: a + b = b + a.
- Trong phép nhân: Đổi chỗ các thừa số trong một tích không làm thay đổi tích đó. Ví dụ: a * b = b * a.
- Tính chất kết hợp:
- Về phép cộng: Khi cộng một tổng của hai số với một số thứ ba, bạn có thể cộng số thứ nhất với số thứ hai trước, rồi cộng kết quả với số thứ ba. Ví dụ: (a + b) + c = a + (b + c).
- Về phép nhân: Khi nhân một tích của hai số với một số thứ ba, bạn có thể nhân số thứ nhất với tích của số thứ hai và số thứ ba. Ví dụ: (a * b) * c = a * (b * c).
- Tính chất phân phối: Đối với phép nhân và phép cộng: Để nhân một số với một tổng, bạn có thể nhân số đó với từng số hạng của tổng rồi cộng tất cả các kết quả lại. Ví dụ: a * (b + c) = (a * b) + (a * c).
1.4. Phép trừ và phép chia
- Điều kiện thực hiện phép trừ: Để thực hiện phép trừ, số bị trừ cần phải lớn hơn hoặc bằng số trừ. Nếu không, phép trừ không thực hiện được trong tập số tự nhiên. Ví dụ: 3 - 5 không thể thực hiện trong tập số tự nhiên.
- Điều kiện để một số a chia hết cho số b (a, b ∈ N, b ≠ 0) là phải có một số tự nhiên q sao cho a = b * q. Nói cách khác, số b phải là ước của số a. Ví dụ: 10 chia hết cho 2 vì tồn tại số tự nhiên 5 sao cho 10 = 2 * 5.
- Đặc điểm của phép chia có dư: Trong phép chia có dư, số bị chia có thể được biểu diễn dưới dạng tổng của tích số chia và thương, cộng với số dư. Cụ thể, số bị chia = số chia * thương + số dư, với số chia khác 0 và số dư nhỏ hơn số chia. Ví dụ: 10 = 3 * 3 + 1 là phép chia có dư, trong đó số chia là 3, thương là 3 và số dư là 1.
1.5. Lũy thừa và số mũ tự nhiên
- Lũy thừa bậc n của số a: Lũy thừa bậc n của một số a là tích của n bản sao của số a. Ví dụ: a^n = a * a * ... * a (n lần nhân), với n là số nguyên dương.
- Quy tắc nhân lũy thừa: Khi nhân hai lũy thừa có cùng cơ số, bạn giữ nguyên cơ số và cộng các số mũ với nhau. Ví dụ: a^m * a^n = a^(m+n), với m và n là số nguyên.
- Quy tắc chia lũy thừa: Khi thực hiện phép chia giữa hai lũy thừa có cùng cơ số, bạn giữ nguyên cơ số và trừ số mũ của lũy thừa thứ hai từ số mũ của lũy thừa đầu tiên. Ví dụ: a^m / a^n = a^(m-n), với m và n là các số nguyên.
- Quy ước đặc biệt: a^0 = 1 (với a ≠ 0). Mọi số được mũ 0 đều bằng 1, ngoại trừ trường hợp 0^0 vì nó không xác định.
1.6. Các dấu hiệu chia hết cho 2, 5, 3, 9
- Chia hết cho 2: Nếu chữ số cuối cùng của số là một số chẵn như 0, 2, 4, 6 hoặc 8, thì số đó chia hết cho 2. Ngược lại, nếu chữ số cuối cùng là số lẻ, thì số đó không chia hết cho 2.
- Chia hết cho 5: Nếu chữ số cuối cùng của số là 0 hoặc 5, thì số đó chia hết cho 5. Ngược lại, nếu chữ số cuối cùng không phải là 0 hoặc 5, thì số đó không chia hết cho 5.
- Chia hết cho 9: Một số chia hết cho 9 nếu tổng các chữ số của nó chia hết cho 9. Ví dụ: 135 (1 + 3 + 5 = 9) và 1,098 (1 + 0 + 9 + 8 = 18) đều chia hết cho 9. Ngược lại, nếu tổng các chữ số không chia hết cho 9, số đó không chia hết cho 9.
- Chia hết cho 3: Tương tự như quy tắc chia hết cho 9, một số chia hết cho 3 nếu tổng các chữ số của nó chia hết cho 3. Ví dụ: 123 (1 + 2 + 3 = 6) và 990 (9 + 9 + 0 = 18) đều chia hết cho 3. Ngược lại, nếu tổng các chữ số không chia hết cho 3, số đó không chia hết cho 3.
1.7. Ước và bội, số nguyên tố, phân tích số thành thừa số nguyên tố
- Bội số và ước số:
- Nếu số tự nhiên a chia hết cho số tự nhiên b, thì a là bội số của b, còn b là ước số của a.
- Để tìm bội số của một số, bạn nhân số đó với các số tự nhiên như 0, 1, 2, 3,... Bội số của số b có dạng b.k với k là số tự nhiên.
- Để xác định ước số của một số, bạn chia số đó cho các số tự nhiên như 1, 2, 3,... và kiểm tra xem số đó có chia hết cho các số này không.
- Số nguyên tố và hợp số:
- Số nguyên tố là các số tự nhiên lớn hơn 1, chỉ có hai ước số duy nhất là 1 và chính nó. Số nguyên tố chẵn duy nhất là số 2.
- Số hợp số là các số tự nhiên lớn hơn 1 có ít nhất một ước số khác 1 và khác chính nó.
- Phân tích thành thừa số nguyên tố:
- Để phân tích một số tự nhiên thành các thừa số nguyên tố, ta biểu diễn số đó dưới dạng tích của các thừa số nguyên tố.
- Mọi số tự nhiên lớn hơn 1 đều có thể phân tích thành tích của các thừa số nguyên tố.
1.8. Ước chung và bội chung
- Ước chung và bội chung:
- Ước chung của hai hoặc nhiều số là số mà tất cả các số đó đều chia hết.
- Bội chung của hai hoặc nhiều số là số mà tất cả các số đó đều là ước số của nó.
- Ước chung lớn nhất (ƯCLN) là số lớn nhất trong tập hợp các ước chung của hai hoặc nhiều số.
- Bội chung nhỏ nhất (BCNN) là số nhỏ nhất khác 0 trong tập hợp các bội chung của hai hoặc nhiều số.
- Phương pháp tính ƯCLN:
- Chia mỗi số thành tích của các thừa số nguyên tố.
- Chọn các thừa số nguyên tố chung giữa các số.
- Tính tích của các thừa số đó với số mũ nhỏ nhất của chúng để tìm ƯCLN.
- Phương pháp tính BCNN:
- Phân tích từng số thành tích của các thừa số nguyên tố cơ bản.
- Chọn các thừa số nguyên tố chung và riêng giữa các số đó.
- Tính tích của những thừa số này với số mũ lớn nhất của chúng để xác định BCNN.
- Đặc điểm của ƯCLN và BCNN:
- Hai số có ƯCLN bằng 1 khi chúng không có ước chung nào ngoài 1, tức là chúng là các số nguyên tố cùng nhau.
- ƯCLN của tập hợp số là số nhỏ nhất nếu nó chia hết cho tất cả các số trong tập hợp.
- BCNN của tập hợp số là số lớn nhất nếu nó là bội của tất cả các số trong tập hợp.
1.9. Số nguyên
- Tập hợp số nguyên (Z): Bao gồm các số nguyên dương, số nguyên âm và số 0.
- Số đối: Đối của một số nguyên a là -a. Ví dụ, số đối của +1 là -1.
- Giá trị tuyệt đối: Giá trị tuyệt đối của một số nguyên a là khoảng cách từ số đó đến 0 trên trục số, ký hiệu là |a|. Ví dụ: | -20 | = 20, |13| = 13.
- Quy tắc cộng:
- Cộng hai số nguyên cùng dấu: Tương đương với việc cộng hai số tự nhiên dương. Ví dụ: (+4) + (+2) = 4 + 2 = 6.
- Cộng hai số nguyên trái dấu: So sánh giá trị tuyệt đối của hai số, lấy hiệu giữa chúng và gán dấu của số có giá trị lớn hơn. Ví dụ: (-17) + (-55) = -(17 + 55) = -72.
2. Hệ thống kiến thức môn Toán lớp 6 học kỳ 1 phần hình học
2.1. Điểm và đường thẳng
| Cách viết thông thường | Hình vẽ | Ký hiệu |
| Điểm M | M | |
| Đường thẳng a | A | |
| Điểm M thuộc a | M ∈ d | |
| Điểm N không thuộc a | N ∈ d |
2.2. Ba điểm thẳng hàng
Khi ba điểm nằm trên cùng một đường thẳng, chúng được gọi là thẳng hàng. Trong trường hợp này, chỉ có một điểm nằm giữa hai điểm còn lại.
Ví dụ: Xét ba điểm M, N, và P nằm trên cùng một đường thẳng. Khi đó:
- Điểm N và điểm P nằm cùng một phía so với điểm M trên đường thẳng.
- Điểm M và điểm P cũng nằm cùng một phía so với điểm N trên đường thẳng.
Điểm nằm giữa hai điểm còn lại trên một đường thẳng được gọi là điểm chính giữa.
2.3. Đường thẳng qua hai điểm
Khi có hai điểm khác biệt, chỉ tồn tại duy nhất một đường thẳng có thể đi qua cả hai điểm đó. Đây là nguyên lý độc nhất của đường thẳng.
Hai đường thẳng khác nhau được gọi là hai đường thẳng phân biệt. Có hai tình huống có thể xảy ra:
- Hai đường thẳng có một điểm chung duy nhất: Đây là trường hợp hai đường thẳng cắt nhau, và điểm giao nhau là điểm mà cả hai đường thẳng đều đi qua.
- Hai đường thẳng không có điểm chung: Đây là trường hợp hai đường thẳng song song, không bao giờ cắt nhau và không có điểm chung.
2.4. Tia
- Một tia gốc O (hay còn gọi là nửa đường thẳng gốc O) là một phần của đường thẳng bắt đầu từ điểm O và mở rộng về một phía. Tia gốc O được ký hiệu là tia Ox, với O là gốc và x là điểm nằm trên tia.
- Hai tia Ox và Oy có cùng gốc O và hợp thành một đường thẳng xy. Hai tia đối nhau là những tia có chung gốc O, được ký hiệu là tia Ox và tia Oy. Mọi điểm trên đường thẳng xy đều là điểm chung của hai tia đối nhau Ox và Oy.
- Hai tia phân biệt là những tia không trùng nhau và không có điểm chung, nghĩa là chúng không chồng lắp lên nhau và không có điểm nào mà cả hai tia đều đi qua.
2.5. Đoạn thẳng và độ dài đoạn thẳng
- Đoạn thẳng AB được xác định bởi hai điểm A và B và bao gồm tất cả các điểm nằm trên đường thẳng AB giữa hai điểm đó. Điểm A và B là hai đầu của đoạn thẳng AB. Khi nói về đoạn thẳng AB, chúng ta chỉ xem xét các điểm nằm trên đoạn thẳng này, không bao gồm các điểm ngoài đoạn thẳng. Độ dài của đoạn thẳng AB là khoảng cách giữa hai điểm A và B.
- Nếu hai đoạn thẳng có độ dài giống nhau, chúng được ký hiệu là AB = CD. Điều này có nghĩa là đoạn thẳng AB và đoạn thẳng CD có cùng khoảng cách giữa các điểm đầu và cuối của chúng.
2.6. Khi nào thì AM + MB = AB?
Nếu điểm M nằm giữa hai điểm A và B trên cùng một đường thẳng, ta có thể tính AM + MB = AB. Đây là tính chất cơ bản của đoạn thẳng và vị trí điểm giữa. Ngược lại, nếu AM + MB = AB, thì điểm M nhất định phải nằm giữa hai điểm A và B. Điều này đúng vì AM + MB chính là tổng khoảng cách từ M đến A và từ M đến B, và nó phải bằng khoảng cách từ A đến B nếu M nằm giữa A và B.
2.7. Vẽ đoạn thẳng theo độ dài cho trước
- Trên tia Ox, với bất kỳ giá trị dương a nào, ta luôn có thể xác định được một điểm M sao cho OM = a. Điều này có nghĩa là từ điểm O, ta có thể di chuyển một khoảng a đơn vị theo hướng dương của tia Ox để tới điểm M.
- Nếu trên tia Ox có hai điểm M và N với OM = a và ON = b, trong đó a < b, thì điểm M sẽ nằm giữa điểm O và điểm N trên tia Ox. Khoảng cách từ O đến M (OM) sẽ nhỏ hơn khoảng cách từ O đến N (ON), chứng tỏ M gần điểm O hơn N.
2.8. Trung điểm của đoạn thẳng
Trung điểm M của đoạn thẳng AB là điểm nằm chính giữa đoạn thẳng, và cách đều hai điểm A và B. Khi đó, MA = MB, nghĩa là khoảng cách từ M đến A bằng khoảng cách từ M đến B. Trung điểm chia đoạn thẳng AB thành hai đoạn bằng nhau về độ dài.
3. Đề thi học kỳ 1 môn Toán lớp 6 (kèm đáp án)
I. Phần trắc nghiệm (2 điểm)
Câu 1: Số lượng phần tử trong tập hợp A = {1; 5; 6; 8; 10} là:
A) 10
B) 4
C) 5
D) 2
Câu 2: Số nào dưới đây chia hết cho 3?
A) 26
B) 223
C) 109
D) 2019
Câu 3: Kết quả của phép tính 34.32 là bao nhiêu?
A) 36
B) 32
C) 38
D) -3
Câu 4: Số đối của 3 là gì?
A) 3
B) -3
C) 1
D) -1
Câu 5: Trong số các biển báo dưới đây, biển báo nào có tính đối xứng trục?
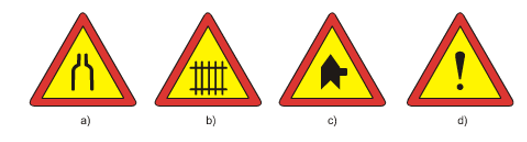
B) b, c, d.
C) a, c, d.
D) a, b, d.
Câu 6: Trong các số 2, 3, 6, 8, số nào là ước chung của cả 6 và 16?
A) 3
B) 2
C) 6
D) Hình số 8
Câu 7: Trong các hình dưới đây, hình nào có tính chất đối xứng qua tâm?
a) Tam giác đều
b) Cánh quạt
c) Hình cánh diều
d) Hình trái tim.
Câu 8: Khẳng định nào dưới đây là không đúng?
a) Trong tam giác đều, tất cả các góc đều bằng nhau.
b) Hình lục giác đều có ba đường chéo chính bằng nhau.
c) Trong hình thoi, hai đường chéo vuông góc với nhau.
d) Hình thang cân có hai góc kề cạnh bên bằng nhau.
II. Phần tự luận
Bài 1 (2 điểm): Thực hiện các phép tính sau đây:
a) (4 + 32 + 6) + (10 – 32 – 2)
b) 300 chia 4 cộng 300 chia 6 trừ 25
c) 17.[29 – (-111)] + 29.(-17)
d) 19.43 + (-20).43 + 40
Bài 2 (1,5 điểm): Tìm giá trị của x:
a) 200 – 8.(2x + 7) = 112
b) (2x – 123) chia 3 = 33
c) H = {x ∈ ℤ | -3 < x ≤ 3}
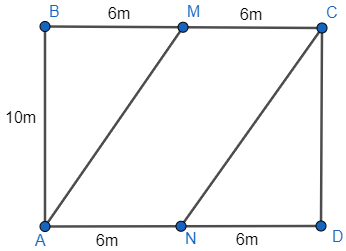
Bài 3 (2 điểm): Trên một mảnh đất hình chữ nhật dài 12m, rộng 10m, được chia thành khu vực trồng hoa và trồng cỏ như hình vẽ. Hoa được trồng trong khu vực hình bình hành AMCN, còn cỏ sẽ được trồng ở phần đất còn lại. Tiền công trồng hoa là 50.000 đồng/m² và trồng cỏ là 40.000 đồng/m². Tính tổng số tiền công cần chi trả để trồng hoa và cỏ.
Bài 4 (2 điểm): Trong dịp Tết trồng cây, ba nhóm học sinh lớp 6 tham gia trồng cây. Mỗi học sinh của nhóm đầu tiên trồng 8 cây, nhóm thứ hai trồng 9 cây, và nhóm thứ ba trồng 12 cây. Tính số cây mỗi nhóm đã trồng, biết rằng số cây trồng của mỗi nhóm nằm trong khoảng từ 200 đến 250 cây.
Bài 5 (0,5 điểm): Xét A = 7 + 72 + 73 + ... + 7119 + 7120. Chứng minh rằng A chia hết cho 57.
ĐÁP ÁN:
I. Phần trắc nghiệm
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| C | D | A | B | D | B | B | D |
II. Phần tự luận
Bài 1:
a) (4 + 32 + 6) + (10 – 32 – 2) = (36 + 6) + (-22 – 2) = 42 + (-24) = 42 – 24 = 18
b) 300:4 + 300:6 – 25 = 75 + 50 – 25 = 125 – 25 = 100
c) 17.[29 – (-111)] + 29.(-17) = 17.(29 + 111) – 29.17 = 17.29 + 17.111 – 29.17 = (17.29 – 29.17) + 17.111 = 0 + 1887 = 1887
d) 19.43 + (-20).43 – (-40) = 19.43 – 20.43 + 40 = 43(19 – 20) + 40 = 43.(-1) + 40 = -43 + 40 = -3
Bài 2:
a) 200 – 8.(2x + 7) = 112
-8.(2x + 7) = 112 – 200
-8.(2x + 7) = -88
2x + 7 = (-88):(-8)
2x + 7 = 11
2x = 11 – 7
2x = 4
x = 4 chia 2
x = 2
b) (2x – 123):3 = 33
2x – 123 = 33 nhân 3
2x – 123 = 99
2x = 99 cộng 123
2x = 222
x = 222 chia 2
x = 111
c) H = {x ∈ ℤ | -3 < x ≤ 3}
Vì H = nên H = {-2; -1; 0; 1; 2; 3}
Vậy x ∈ {-2; -1; 0; 1; 2; 3}
Bài 3
Rõ ràng, trong hình bình hành AMCN, chiều cao tương ứng với cạnh AN chính là MN và MN = AB = 10m
Vì vậy, diện tích của hình bình hành AMCN là: 6 x 10 = 60 (m2)
Diện tích của hình chữ nhật ABCD là: 10 x 12 = 120 (m2)
Diện tích còn lại để trồng cỏ là: 120 - 60 = 60 (m2)
Chi phí để trồng hoa là: 50.000 x 60 = 3.000.000 (đồng)
Chi phí để trồng cỏ là: 40.000 x 60 = 2.400.000 (đồng)
Tổng số tiền cần chi trả để trồng hoa và cỏ là: 3.000.000 + 2.400.000 = 5.400.000 (đồng)
Như vậy, tổng số tiền cần để trồng hoa và cỏ là 5.400.000 đồng.
Bài 4
Gọi số cây mà mỗi nhóm trồng được là x (x ∈ ℕ*; 200 < x < 250)
Mỗi thành viên nhóm đầu tiên trồng 8 cây, nhóm thứ hai trồng 9 cây, và nhóm thứ ba trồng 12 cây, do đó,
x chia hết cho 8 nên x là bội số của 8
x chia hết cho 9 nên x là bội số của 9
x chia hết cho 12 nên x là bội số của 12
Do đó, số cây mà mỗi nhóm trồng được là bội số chung của 8, 9 và 12.
Chúng ta có:
8 = 2 x 2 x 2 = 2^3
9 = 3 x 3 = 3^2
12 = 3 x 2 x 2 = 3 x 2^2
BCNN(8, 9, 12) = 2^3 x 3^2 = 72
Vậy BCNN(8, 9, 12) =
Do số cây mỗi nhóm trồng nằm trong khoảng từ 200 đến 250, số cây mà mỗi nhóm trồng được là 216 cây.
Vì vậy, mỗi nhóm trồng được 216 cây.
Bài 5
A = 7 + 72 + 73 + ... + 7119 + 7120
A = (71 + 72 + 73) + (74 + 75 + 76) + ... + (7118 + 7119 + 7120)
A = 7(1 + 7 + 72) + 74(1 + 7 + 72) + ... + 7118(1 + 7 + 72)
A = 7 × 57 + 74 × 57 + ... + 7118 × 57
A = 57 × (7 + 74 + ... + 7118)
Vì 57 chia hết cho 57, nên 57 × (7 + 74 + ... + 7118) cũng chia hết cho 57
Vì vậy, A chia hết cho 57 (điều này cần được chứng minh)
- Đề thi học kỳ 2 môn Toán lớp 6 sách Cánh diều với đáp án
- Đề thi học kỳ 2 Toán lớp 6 với đáp án được chọn lọc mới nhất
Hy vọng những thông tin chia sẻ từ Mytour giúp bạn đọc có cái nhìn rõ hơn về hệ thống kiến thức môn Toán lớp 6 học kỳ 1 một cách chi tiết và đầy đủ. Chúng tôi mong rằng bài viết này sẽ là tài liệu tham khảo hữu ích cho bạn, chúc bạn có một học kỳ hiệu quả và đạt kết quả cao.
