Bộ sưu tập bài toán hình học lớp 9 với đáp án cập nhật mới nhất

1. Bài 1 - Bài tập hình học lớp 9

1. Cho tam giác ABC với ba góc nhọn tiếp xúc với đường tròn (O). Các đường cao AD, BE, CF giao nhau tại H và cắt đường tròn (O) tại M, N, P.

a. Chứng minh rằng tứ giác CEHD là tứ giác nội tiếp

b. Các điểm B, C, E, F đều nằm trên một đường tròn.

c. AE × AC = AH × AD ; AD × BC = BE × AC

d. H và M là hai điểm đối xứng qua BC

e. Tìm tâm của đường tròn nội tiếp tam giác DÈ.

Hướng dẫn giải:

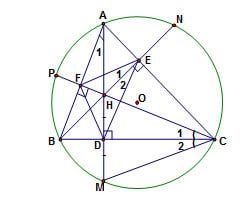
a. Xem xét tứ giác CEHD, ta có:

Góc CEH = 90⁰ vì BE là đường cao.

Góc CDH = 90⁰ vì AD là đường cao.

Do đó, góc CEH cộng góc CDH bằng 180⁰.

Góc CEH và góc CDH là hai góc đối diện trong tứ giác CEHD, do đó CEHD là tứ giác nội tiếp.

2. Theo giả thiết: BE là đường cao.

Do đó, BE vuông góc với AC.

Vì vậy, góc BEC = 90⁰.

CF là đường cao.

Do đó, CF vuông góc với AB.

Vì vậy, góc BCF = 90⁰.

Như vậy, E và F cùng nhìn BC dưới một góc 90 độ.

Do đó, E và F đều nằm trên đường tròn có đường kính BC.

Vậy bốn điểm B, C, E, F đều nằm trên cùng một đường tròn.

3. Xem xét hai tam giác AEH và ADC, ta có:

Góc AEH bằng góc ADC, đều bằng 90⁰.

Góc A là góc chung của hai tam giác.

Suy ra: AE // AD và AH // AC, do đó AE . AC = AH . AD

- Xem xét hai tam giác BEC và ADC, ta có:

Góc BEC bằng góc ADC, đều bằng 90⁰, và góc C là góc chung.

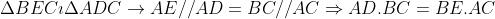
d. Ta có: góc C1 = góc A1 vì chúng đều bù với góc ABC

Góc C2 = góc A1 vì hai góc nội tiếp cùng chắn cung BM.

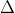
⇒ CB cũng chính là đường trung trực của HM, do đó H và M là hình chiếu đối xứng qua BC.

e. Theo các bước chứng minh trên, bốn điểm B, C, E và F cùng nằm trên một đường tròn.

⇒ góc C1 = góc E1 vì chúng là hai góc nội tiếp cùng chắn cung BF

Như đã chứng minh, CEHD là một tứ giác nội tiếp

Góc C1 = góc E2 vì hai góc nội tiếp cùng chắn cung HD

Góc E1 = góc E2, do đó EB là tia phân giác của góc FED

Tương tự, ta có FC là tia phân giác của góc DFE. Vì BE và CF cắt nhau tại H, nên H là tâm đường tròn nội tiếp của tam giác DEF.

2. Bài 2 - Bài tập hình học lớp 9

Xét tam giác cân ABC (AB = AC) với các đường cao AD, BE cắt nhau tại H. O là tâm của đường tròn ngoại tiếp tam giác AHE.

a. Chứng minh rằng tứ giác CEHD là tứ giác nội tiếp

b. Xác minh rằng bốn điểm A, E, D và B đều nằm trên một đường tròn.

c. Chứng minh rằng ED = 1/2 BC

d. Chứng minh rằng DE là đường tiếp tuyến với đường tròn (O)

e. Tính chiều dài của DE khi biết DH = 2 cm và AH = 6 cm

Lời giải chi tiết:

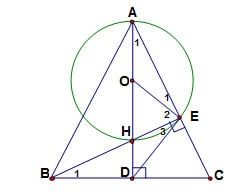
a. Xem xét tứ giác CEHD và ta có:

Góc CEH = 90⁰ do BE là đường cao

Góc CDH = 90⁰ vì AD là đường cao

Như vậy, góc CEH cộng góc CDH bằng 180⁰

Góc CEH và góc CDH là hai góc đối diện của tứ giác CEHD, vì vậy CEHD là tứ giác nội tiếp.

b. Theo giả thuyết, BE là đường cao, do đó BE vuông góc với AC và góc BED = 90⁰

AD là đường cao, vì vậy AD vuông góc với BC. Do đó, góc BDA = 90⁰

Như vậy, E và D cùng nhìn AB dưới một góc 90⁰. Suy ra, E và D cùng nằm trên đường tròn có đường kính AB.

Vì vậy, bốn điểm A, E, D, B đều nằm trên cùng một đường tròn.

c. Theo giả thiết, tam giác ABC cân tại A với AD là đường cao, nên AD cũng là đường trung tuyến.

Do đó, D là trung điểm của BC. Như đã nêu, góc BEC = 90⁰

Do đó, trong tam giác BEC vuông tại E, ED là trung tuyến nên DE = 1/2 BC

d. Vì O là tâm đường tròn ngoại tiếp tam giác AHE, nên O là trung điểm của AH. Do vậy, OA = OE, suy ra tam giác AOE cân tại O. Kết quả là góc E1 = góc A1 (1)

Theo đó, DE = 1/2 BC, dẫn đến tam giác DBE cân tại D, vì vậy góc E3 = góc B1 (2)

Hơn nữa, góc B1 = góc A1 vì cùng phụ với góc ACB, suy ra góc E1 = góc E3, và vì vậy góc E1 + góc E2 = góc E2 + góc E3

Vì góc E1 + góc E2 = góc BEA = 90^o, suy ra góc E2 + góc E3 = 90^o = góc OED

Do đó, DE vuông góc với OE tại E

Như vậy, DE là tiếp tuyến của đường tròn (O) tại điểm E.

e. Theo giả thiết, AH = 6 cm

Suy ra OH = OE = 3 cm và DH = 2 cm, nên OD = 5 cm

Áp dụng định lý Pythagoras cho tam giác OED vuông tại E

Ta có: ED² = OD² - OE² ⇒ ED² = 5² - 3² ⇒ ED = 4 cm

3. Các dạng bài toán tham khảo

1. Cho đường tròn (O; R), từ một điểm A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d, chọn điểm M khác A, vẽ cắt tuyến MNP và gọi K là trung điểm của NP. Kẻ tiếp tuyến MB (B là điểm tiếp xúc). Vẽ các đường AC - MB, BD - MA, và gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB.

a. Chứng minh rằng tứ giác AMBO là tứ giác nội tiếp

b. Chứng minh rằng năm điểm O, K, A, M, B đều nằm trên cùng một đường tròn

c. Chứng minh rằng OI · OM = R² và OI · IM = IA²

d. Chứng minh rằng OAHB là hình thoi.

e. Chứng minh ba điểm O, H, M nằm trên cùng một đường thẳng.

f. Xác định quỹ tích của điểm H khi điểm M di chuyển trên đường thẳng d.

2. Từ kết quả trên, ta thấy rằng OAHB là hình thoi với AH = AO = R. Khi M thay đổi vị trí trên đường d, H cũng di chuyển nhưng luôn giữ khoảng cách cố định với A bằng R. Do đó, quỹ tích của điểm H khi M di chuyển trên đường thẳng d là nửa đường tròn có tâm A và bán kính AH = R.

3. Xét tam giác ABC vuông tại A với đường cao AH. Vẽ một đường tròn nội tiếp có tâm tại A và bán kính AH. Gọi HD là đường kính của đường tròn (A; AH). Tiếp tuyến của đường tròn tại D cắt cạnh CA tại E.

a. Chứng minh rằng tam giác BEC là tam giác cân.

b. Gọi I là hình chiếu của A lên BE, chứng minh rằng AI = AH.

c. Chứng minh rằng BE là tiếp tuyến của đường tròn (A; AH).

d. Chứng minh rằng BE = BH + DE.

4. Xét tam giác cân ABC với AB = AC, các đường cao AD và BE cắt nhau tại điểm H. Gọi O là tâm của đường tròn ngoại tiếp tam giác AHE.

a. Chứng minh rằng tứ giác CEHD là tứ giác nội tiếp.

b. Các điểm A, E, D, B nằm trên cùng một đường tròn.

c. Chứng minh rằng ED = 1/2 BC.

d. Chứng minh rằng DE là tiếp tuyến của đường tròn (O).

e. Tính độ dài của DE biết DH = 2 cm và AH = 6 cm.

5. Xét tam giác cân ABC với AB = AC, I là tâm đường tròn nội tiếp, K là tâm của đường tròn tiếp xúc với góc A, và O là trung điểm của IK.

a. Chứng minh rằng các điểm B, C, I, K nằm trên cùng một đường tròn.

b. Chứng minh rằng AC là tiếp tuyến của đường tròn (O).

c. Tính bán kính của đường tròn (O) biết AB = AC = 20 cm và BC = 24 cm.

6. Cho đường tròn (O; R). Từ điểm A trên đường tròn, vẽ tiếp tuyến d tại A. Trên đường thẳng d, chọn điểm M khác A, vẽ cát tuyến MNP và gọi K là trung điểm của NP. Vẽ tiếp tuyến MB tại điểm B, vẽ AC vuông góc với MB và BD vuông góc với MA. Gọi H là giao điểm của AC và BD, I là giao điểm của OM với AB.

a. Chứng minh rằng tứ giác AMBO là tứ giác nội tiếp.

b. Chứng minh rằng năm điểm O, K, A, M, B đều nằm trên một đường tròn.

c. Chứng minh rằng OI × OM = R² và OI × IM = IA²

d. Chứng minh rằng OAHV là hình thoi.

e. Chứng minh rằng ba điểm O, H và M nằm trên một đường thẳng.

f. Xác định quỹ tích của điểm H khi điểm M thay đổi trên đường thẳng d.

Bạn đọc có thể tải xuống tuyển tập các bài toán hình học lớp 9 qua liên kết sau: Tại đây