Các dạng bài Toán thực tiễn thường gặp trong kỳ thi vào lớp 10

Buzz

Nội dung bài viết

1. Dạng 1. Bài toán thực tiễn về chuyển động

2. Loại 2. Bài toán thực tế liên quan đến năng suất và công việc

3. Dạng 3. Bài toán thực tế liên quan đến lĩnh vực kinh doanh

4. Dạng 4: Bài toán thực tế liên quan đến hình học

5. Dạng 5. Bài toán thực tế liên quan đến hóa học

6. Dạng 6: Bài toán thực tế liên quan đến môn Vật lý.

Xem thêm

Dưới đây là thông tin chi tiết về các bài toán thực tiễn phổ biến trong kỳ thi tuyển sinh lớp 10, được Mytour gửi đến các bạn đọc. Hy vọng rằng bài viết này sẽ hỗ trợ các em học sinh ôn tập hiệu quả.

1. Dạng 1. Bài toán thực tiễn về chuyển động

Phương pháp giải: Cần chú ý đến công thức S = vt, trong đó S là quãng đường, v là vận tốc và t là thời gian. Bên cạnh đó, áp dụng nguyên lý cộng vận tốc cho các bài toán về tàu thuyền trên mặt nước, ta có:

- Vận tốc xuôi dòng = Vận tốc thực tế + Vận tốc của dòng nước.

- Vận tốc ngược dòng = Vận tốc thực tế - Vận tốc của dòng nước.

- Vận tốc thực tế luôn lớn hơn vận tốc của dòng nước.

Bài tập ứng dụng: Hai chiếc ca nô xuất phát từ điểm A và B, cách nhau 85 km, và di chuyển về hướng ngược nhau. Sau 1 giờ 40 phút, chúng gặp nhau. Tính vận tốc của từng chiếc ca nô khi nước đứng yên, biết rằng ca nô đi xuôi dòng nhanh hơn ca nô đi ngược dòng 9 km/h và vận tốc dòng nước là 3 km/h.

Hướng dẫn giải:

Gọi vận tốc thực tế của ca nô đi xuôi dòng từ A là x (km/h) (x > 6), do đó, vận tốc của ca nô khi đi xuôi dòng là x + 3 (km/h).

Gọi vận tốc thực tế của ca nô di chuyển ngược dòng từ B là y (km/h) (y > 3), vì vậy vận tốc của ca nô đi ngược dòng sẽ là y - 3 (km/h).

Vận tốc của ca nô đi xuôi dòng lớn hơn vận tốc của ca nô đi ngược dòng 9 km/h, ta thiết lập phương trình: x + 3 - (y - 3) = 9 ⇔ x - y = 3 (1)

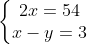
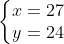
$\frac{5}{3}$ $\frac{5}{3}$ $\frac{5}{3}$ $\frac{5}{3}$ $\frac{5}{3}$ $\frac{5}{3}$ $\frac{5}{3}$ $\frac{5}{3}$ $\left\{\begin{matrix} x - y = 3 & \\ x + y = 51 & \end{matrix}\right.$ $\left\{\begin{matrix} 2x = 54 & \\ x - y = 3 & \end{matrix}\right.$ $\left\{\begin{matrix} x = 27 & \\ y = 24 & \end{matrix}\right.$

Do đó, vận tốc thực của ca nô khi đi xuôi dòng là 27 km/h, còn khi đi ngược dòng là 24 km/h.

2. Loại 2. Bài toán thực tế liên quan đến năng suất và công việc

Phương pháp giải quyết:

- Xem khối lượng công việc như một đơn vị

- NS 1 cộng NS 2 bằng tổng NS

$\frac{1}{x}$ $\frac{1}{x}$ $\frac{1}{x}$

Bài tập ứng dụng: Hai nhóm công nhân cùng thực hiện một công việc và hoàn thành trong 4 giờ. Nếu mỗi nhóm làm việc riêng lẻ, nhóm đầu tiên cần ít thời gian hơn nhóm thứ hai là 6 giờ. Tìm thời gian mà mỗi nhóm cần để hoàn thành công việc khi làm riêng.

Giải pháp:

Gọi thời gian để nhóm đầu tiên hoàn thành công việc một mình là: x (giờ), với điều kiện x > 4

Vậy thời gian để nhóm thứ hai hoàn thành công việc một mình là: x + 6 (giờ)

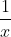
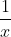
$\frac{1}{x}$ $\frac{1}{x + 6}$ $\frac{1}{4}$ $\frac{1}{x}$ $\frac{1}{x + 6}$ $\frac{1}{4}$ $x^{2}$ $x^{2}$ $x^{2}$

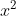
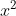
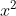
So sánh với điều kiện, x = 6 là giá trị phù hợp.

Do đó, thời gian để đội đầu tiên hoàn thành công việc một mình là 6 giờ, trong khi đội thứ hai cần 12 giờ để hoàn thành công việc một mình.

3. Dạng 3. Bài toán thực tế liên quan đến lĩnh vực kinh doanh

Bài 1. Nhà máy A sản xuất một lô hàng gồm 200 chiếc áo với tổng chi phí là 30.000.000 đồng và giá bán mỗi chiếc áo là 300.000 đồng. Hãy gọi K (đồng) là số tiền lãi (hoặc lỗ) mà nhà máy thu được khi bán t chiếc áo.

a) Xây dựng hàm số K theo biến t.

b) Cần bán bao nhiêu chiếc áo để thu hồi được số vốn đầu tư ban đầu? c) Để có lãi 6.000.000 đồng, cần bán bao nhiêu chiếc áo?

Giải pháp:

a) Hàm số của K theo t được xác định như sau: K = 300000.t - 30000000 (với 0 ≤ t ≤ 200)

b) Để tìm số áo cần bán để thu hồi vốn, thay K = 0 vào công thức K = 300000.t - 30000000, ta có: 0 = 300000.t - 30000000 ⇔ t = 100 (đúng)

Vậy, để thu hồi vốn ban đầu, cần bán 100 chiếc áo.

c) Để có lợi nhuận 6.000.000 đồng, thay K = 6000000 vào công thức K = 300000.t - 30000000, ta có: 6000000 = 300000.t - 30000000 ⇔ t = 120 (đúng)

Do đó, để có lợi nhuận 6.000.000 đồng, cần bán 120 chiếc áo.

Bài 2. Siêu thị AEON MALL Bình Tân đang có chương trình giảm giá cho sản phẩm nước rửa chén Sunlight trà xanh 4,5 lít như sau: Mua 1 can được giảm 8.000 đồng so với giá gốc. Mua 2 can, can đầu tiên giảm 8.000 đồng và can thứ hai giảm 15.000 đồng. Mua từ 3 can trở lên, ngoài hai can đầu được giảm theo mức trên, từ can thứ ba trở đi, mỗi can được giảm 20% so với giá niêm yết. Ông A mua 5 can nước rửa chén Sunlight trà xanh 4,5 lít tại AEON MALL Bình Tân, vậy ông phải trả bao nhiêu tiền, với giá niêm yết là 115.000 đồng/can.

Giải pháp:

Chi phí mua can nước rửa chén Sunlight trà xanh đầu tiên: 115.000 - 8.000 = 107.000 đồng

Chi phí mua can nước rửa chén Sunlight trà xanh thứ hai: 115.000 - 15.000 = 100.000 đồng

Chi phí cho ba can nước rửa chén Sunlight trà xanh còn lại: 115.000 x 80% x 3 = 276.000 đồng

Tổng số tiền ông A phải thanh toán cho 5 can nước rửa chén Sunlight trà xanh là: 107.000 + 100.000 + 276.000 = 483.000 đồng

Kết quả: 483.000 đồng

4. Dạng 4: Bài toán thực tế liên quan đến hình học

Bài 1. Một tàu đánh cá khi ra khơi cần mang theo 50 thùng dầu, mỗi thùng dầu hình trụ với chiều cao 90 cm và đường kính đáy 60 cm. Tính tổng lượng dầu mà tàu cần mang theo khi ra khơi (lấy π ≈ 3,14 và làm tròn đến số nguyên).

Giải pháp:

Bán kính đáy thùng dầu là R = 60 / 2 = 30 (cm)

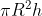
Diện tích đáy thùng được tính bằng công thức πR², với h là chiều cao của thùng

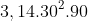
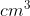
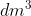
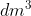
Do đó, tàu cần mang theo 12717 lít dầu khi ra khơi.

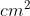
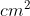
Giải pháp:

Thể tích nước dâng lên trong ly chính là thể tích của bức tượng ngựa đá.

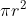
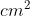
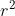
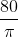
$\frac{80}{π}$

Chiều cao của mực nước dâng lên là h = 1,5 (cm)

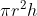
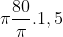
$π × \frac{80}{π} × 1,5$

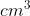
5. Dạng 5. Bài toán thực tế liên quan đến hóa học

Bài 1. Một miếng hợp kim đồng và thiếc nặng 12 kg, trong đó chứa 45% đồng nguyên chất. Tính khối lượng thiếc nguyên chất cần thêm vào để hợp kim mới có 40% đồng nguyên chất?

Lời giải:

Gọi khối lượng thiếc nguyên chất cần thêm là x (kg) (x > 0).

Khối lượng của hợp kim sau khi thêm x kg thiếc nguyên chất là 12 + x (kg).

Vì hợp kim nặng 12 kg chứa 45% đồng nguyên chất nên lượng đồng trong đó là: 12 x 45% = 5,4 kg.

Khi thêm vào thiếc, lượng đồng vẫn không đổi và chiếm 40% tổng khối lượng mới. Ta có phương trình: 40% x (x + 12) = 5,4 ⇔ 0,4x + 4,8 = 5,4 ⇔ 0,4x = 0,6 ⇔ x = 1,5 (đáp án hợp lệ).

Do đó, cần thêm 1,5 kg thiếc nguyên chất để có hợp kim với 40% đồng nguyên chất.

Bài 2. Nước biển có nồng độ muối 3,5% (giả sử không có tạp chất). Có 10 kg nước biển. Cần thêm bao nhiêu kg nước tinh khiết để đạt nồng độ muối 2%?

Lời giải:

Khối lượng muối trong 10 kg nước biển với nồng độ 3,5% là: 10 x 3,5% = 0,35 kg.

Gọi x là số kg nước tinh khiết cần thêm để đạt nồng độ 2%. Ta thiết lập phương trình: (10 + x) x 2% = 0,35.

Giải phương trình trên, ta tìm được x = 7,5.

6. Dạng 6: Bài toán thực tế liên quan đến môn Vật lý.

$t^{2}$

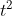
a) Sau 2 giây, khoảng cách của vật từ mặt đất là bao nhiêu mét?

b) Vật này sẽ chạm đất sau bao lâu?

Lời giải:

$2^{2}$

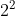
Vậy sau 2 giây, vật này còn cách mặt đất 84 mét (tính từ độ cao ban đầu 100 mét).

$t^{2}$ $t^{2}$

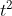
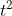
Do đó, vật sẽ chạm đất sau 5 giây.

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]