Buzz
1. Khám phá đề thi tuyển sinh môn Toán lớp 10
1.1. Phạm vi kiến thức
Đề thi môn Toán vào lớp 10 thường bám sát chương trình THCS, đặc biệt là lớp 9 theo quy định của Bộ GD&ĐT. Đề thi cần đánh giá đa dạng các cấp độ nhận thức của học sinh, bao gồm nhận biết, hiểu biết, vận dụng và vận dụng cao. Thời gian làm bài thi cũng được điều chỉnh phù hợp với yêu cầu kiến thức của đề.
1.2. Độ khó của đề thi
Do ảnh hưởng của dịch bệnh trong các năm qua, các đề thi trước đây đã được điều chỉnh để dễ hơn. Tuy nhiên, theo thông báo từ Sở GD&ĐT Hà Nội, đề thi sắp tới sẽ tập trung vào các câu hỏi theo chuẩn kiến thức của Bộ GD&ĐT, chủ yếu là chương trình lớp 9 và không yêu cầu kiến thức giảm tải.
Thêm vào đó, theo định hướng của Bộ GD&ĐT, đề thi sẽ tập trung vào những phần kiến thức cơ bản và không bao gồm các phần kiến thức đã giảm tải. Điều này nhằm giúp học sinh ôn tập hiệu quả hơn.
1.3. Cấu trúc của đề thi
Dựa trên đề thi của các tỉnh thành, cấu trúc đề thi môn Toán vào lớp 10 có thể được phân thành bốn nhóm chính như sau:
Nhóm 1 (hay nhóm T1): bao gồm các câu hỏi ở mức độ cơ bản, thường là nhận biết hoặc thông hiểu.
Nhóm 2 (hay nhóm T2): đòi hỏi các yêu cầu ở mức độ khá, cần có khả năng vận dụng tốt kiến thức.
Nhóm 3: tập trung vào các yêu cầu ở mức độ cao, chủ yếu dành cho học sinh tại Hà Nội.
Nhóm 4: theo cấu trúc đề thi mới, yêu cầu học sinh áp dụng kiến thức vào giải quyết các bài toán thực tiễn, dành riêng cho học sinh tại thành phố Hồ Chí Minh.
2. Đề thi Toán vào lớp 10 được chọn lọc mới nhất
Trong những năm gần đây, dịch Covid-19 đã ảnh hưởng sâu rộng đến nhiều lĩnh vực, bao gồm cả giáo dục. Do đó, cấu trúc và xu hướng đề thi đã có nhiều thay đổi. Theo dõi bài viết của Mytour để cập nhật các dạng đề thi Toán vào lớp 10 mới nhất.
2.1. Đề thi số 01
Câu 1: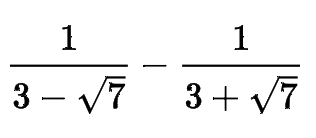
b) Giải phương trình: x2 – 7x + 3 = 0.
Câu 2: a) Xác định tọa độ giao nhau của đường thẳng d: y = -x + 2 và Parabol (P): y = x2.
Câu 3:
Câu 4: Từ điểm A ngoài đường tròn (O; R), ta vẽ hai tiếp tuyến AB và AC với đường tròn (B và C là các điểm tiếp xúc). Trên cung nhỏ BC, chọn điểm M và vẽ các đường vuông góc MI ⊥ AB, MK ⊥ AC (I nằm trên AB, K nằm trên AC).
a) Chứng minh rằng tứ giác AIMK là tứ giác nội tiếp đường tròn.
c) Tìm điểm M trên cung nhỏ BC sao cho tích MI.MK.MP đạt giá trị tối đa.
Câu 5: Giải phương trình sau:
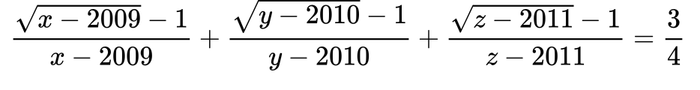
2.2. Đề thi số 02
Câu 1:
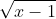
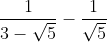
Câu 2: Giải phương trình và bất phương trình sau:
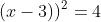
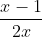Câu 3: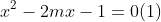 
a) Chứng minh rằng phương trình trên luôn có hai nghiệm phân biệt x1 và x2.
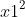
Câu 4: Xét đường tròn (O; R) với đường kính AB. Vẽ dây cung CD vuông góc với AB (CD không đi qua tâm O). Trên tia đối của tia BA, chọn điểm S sao cho SC cắt (O; R) tại điểm M.
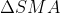
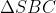
b) Đặt H là điểm giao của MA và BC; K là điểm giao của MD và AB. Chứng minh rằng BMHK là tứ giác nội tiếp và HK song song với CD.
c) Chứng minh rằng: OK \cdot OS = R^2
Câu 5
2.3. Đề số 03
Bài 1: (5 điểm) Giải các phương trình và hệ phương trình dưới đây:
a) 3x^2 - 5x - 8 = 0
b) x^4 - (1 - \sqrt{3})x^2 - \sqrt{3} = 0
Bài 2: (1,5 điểm) Xét Parabol (P) với phương trình y = x^2 và đường thẳng (d) có phương trình y = (2m - 1)x - m + 2 (m là tham số)
a) Vẽ đồ thị của hàm số Parabol (P)
b) Chứng minh rằng với mọi giá trị của m, đường thẳng (d) luôn cắt Parabol (P) tại hai điểm khác biệt. Tìm các giá trị của m để đường thẳng (d) luôn cắt Parabol (P) tại hai điểm phân biệt A(x1; y1) và B(x2; y2) sao cho x1y1 + x2y2 = 0
Bài 3: (1,5 điểm) Xem xét biểu thức sau:
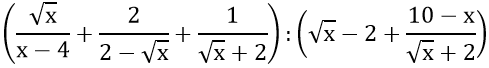
với điều kiện x ≥ 0 và x ≠ 4
a) Rút gọn biểu thức B;
b) Xác định giá trị của x để biểu thức B > 0.
Bài 4: (1,5 điểm)
Một phòng họp có 360 ghế được sắp xếp thành các hàng đều nhau. Tuy nhiên, khi có 400 người đến dự, cần thêm một hàng ghế và mỗi hàng phải thêm một ghế để đủ chỗ. Hãy tính số hàng ghế và số ghế trong mỗi hàng ban đầu.
Bài 5: (3,5 điểm) Cho nửa đường tròn có tâm O và đường kính AB = 2R. Một đường thẳng đi qua O và vuông góc với AB cắt cung AB tại điểm C. Gọi E là trung điểm của đoạn BC, AE cắt nửa đường tròn tại điểm F (F khác A). Đường thẳng qua C và vuông góc với AF cắt AB tại điểm H.
1) Chứng minh tứ giác CGOA là tứ giác nội tiếp và tính số đo của góc OGH.
2) Chứng minh OG là tia phân giác của góc COF.
3) Chứng minh hai tam giác CGO và CFB là đồng dạng.
3. Những điều cần lưu ý khi tham gia kỳ thi Toán vào lớp 10
Chuẩn bị tâm lý vững vàng
Khi ôn tập cho kỳ thi, học sinh cần tập trung để tạo sự tự tin và tránh mắc lỗi trong phòng thi. Đồng thời, nên đến phòng thi sớm để làm quen với không khí và giao tiếp với các bạn cùng phòng, giúp giữ tinh thần thoải mái trước khi bắt đầu.
Đọc qua toàn bộ đề thi và lên kế hoạch làm bài
Nhiều học sinh nhận đề thi và bắt đầu làm ngay mà không đọc qua toàn bộ đề. Đọc qua toàn bộ đề thi là rất quan trọng để xác định thứ tự làm bài, tránh mất thời gian vào các câu khó và bỏ lỡ các câu dễ ở phía dưới.
Kiểm tra đáp án ngay sau khi hoàn thành từng câu
Một điểm quan trọng khác cần lưu ý là 'làm đến đâu, đúng đến đó'. Đặc biệt khi làm các câu hỏi có nhiều phần, nếu phần đầu bị sai và không kiểm tra lại, các phần sau cũng sẽ bị ảnh hưởng, làm cho bài toán trở nên phức tạp hơn.
Tránh mất điểm không đáng có
Khi làm bài thi môn Toán, học sinh cần tránh những lỗi sai phổ biến để không mất điểm đáng tiếc như: tính toán sai; chép sai đề hoặc đọc nhầm; vẽ hình không chính xác hoặc thiếu chi tiết; trình bày quá ngắn gọn; thiếu điều kiện cần thiết hoặc không so sánh với điều kiện đề bài.
Ngoài ra, thực hành với các đề thi của các năm trước là rất quan trọng. Điều này giúp học sinh hiểu rõ cấu trúc và kiểu dáng đề thi, từ đó có thể lập kế hoạch ôn tập hiệu quả. Học sinh nên tham khảo tài liệu của Mytour để luyện tập và đánh giá kiến thức đã ôn.
