Các trường hợp đồng dạng của tam giác vuông và ứng dụng

Buzz

Nội dung bài viết

I. Lý thuyết về các trường hợp đồng dạng của tam giác vuông

II. Loại bài toán về trường hợp đồng dạng của tam giác vuông

III. Bài tập về các trường hợp đồng dạng của tam giác vuông

Xem thêm

Đọc tóm tắt

- Tài liệu quý giá về các trường hợp đồng dạng của tam giác vuông được chia sẻ bởi Mytour cho học sinh lớp 8.
- Tài liệu bao gồm lý thuyết, bài tập và lời giải chi tiết về các trường hợp đồng dạng của tam giác vuông.
- Định lý và tỉ số đường cao, diện tích của hai tam giác đồng dạng.
- Loại bài toán và phương pháp giải.
- Bài tập thực hành với các ví dụ cụ thể và gợi ý đáp án.

Các trường hợp đồng dạng của tam giác vuông là tài liệu quý giá mà Mytour muốn chia sẻ đến quý thầy cô và các bạn học sinh lớp 8. Tài liệu này áp dụng cho cả 3 sách Kết nối tri thức, Cánh diều và Chân trời sáng tạo.

Tổng hợp kiến thức lý thuyết về các trường hợp đồng dạng của tam giác vuông kèm theo các bài tập có đáp án và lời giải chi tiết. Đây là tài liệu hỗ trợ học sinh lớp 8 trong quá trình học tập và ôn luyện tại nhà hiệu quả. Ngoài ra, các em cũng có thể tham khảo thêm: Bài tập về các trường hợp đồng dạng của tam giác.

I. Lý thuyết về các trường hợp đồng dạng của tam giác vuông

Từ các trường hợp đồng dạng của tam giác đã học, có thể suy ra: Hai tam giác vuông đồng dạng nếu thỏa một trong các điều kiện sau:

Một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia;
Hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.

Định lý:

Trường hợp đồng dạng đặc biệt: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đồng dạng.

Tỉ số đường cao, tỉ số diện tích của hai tam giác đồng dạng

Nếu hai tam giác đồng dạng với nhau thì:

+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.

+ Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.

+ Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.

+ Tỉ số chu vi tương ứng bằng tỉ số đồng dạng.

+ Tỉ số diện tích tương ứng bằng bình phương tỉ số đồng dạng.

Ví dụ: Cho tam giác đồng dạng với tam giác ABC theo tỉ số k = 4/3. Tính chu vi của tam giác ABC, biết chu vi của tam giác A'B'C' bằng 27cm.

II. Loại bài toán về trường hợp đồng dạng của tam giác vuông

Bài toán 1: Áp dụng tam giác đồng dạng, tỉ số đường cao và tỉ số diện tích để tính toán.

Phương pháp:

+ Dựa vào tam giác đồng dạng, suy ra các cặp cạnh tỉ lệ và các góc tương đương, từ đó suy ra tỉ số diện tích và tỉ số đường cao.

+ Từ đó, tính các cạnh, góc và điều kiện cần thiết.

Bài toán 2: Chứng minh hai tam giác đồng dạng và các vấn đề liên quan.

Phương pháp:

+ Áp dụng các trường hợp đồng dạng của tam giác để chứng minh tam giác đồng dạng.

+ Từ đó suy ra các hệ thức cần chứng minh.

III. Bài tập về các trường hợp đồng dạng của tam giác vuông

Bài 1: Cho một tam giác vuông, trong đó cạnh huyền dài 20cm và một cạnh góc vuông dài 12cm. Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền.

Gợi ý đáp án

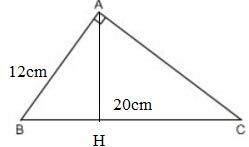
∆ABC vuông tại A có đường cao AH, BC = 20cm, AB = 12cm. Ta tính HC.

Ta có: ∆ABH tương đồng ∆CBA vì:

$\widehat B$ $\widehat{H} = \widehat{A}=90^o$ $\Rightarrow \dfrac{AB}{CB}= \dfrac{BH}{BA}$ $\Rightarrow AB^2= HB.CB$ $\Rightarrow BH = \dfrac{AB^{2}}{CB}= \dfrac{12^{2}}{20} = 7,2 \,(cm)$ $\Rightarrow CH = BC - BH = 20 - 7,2 = 12,8\,cm$

Bài 2: Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành hai đoạn thẳng có độ dài 25cm và 36cm. Tính chu vi và diện tích của tam giác vuông đó

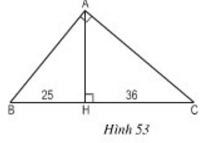
Gợi ý đáp án

$\widehat{AHB} = \widehat{AHC}=90^o , \widehat{BAH} = \widehat{ACH}$ $\widehat {HAC}$ $\Rightarrow \dfrac{AH}{CH }= \dfrac{BH}{AH}$ $\Rightarrow A{H^2}=CH.BH = 25.36$ $\Rightarrow A{H^2}= 900 \Rightarrow AH = 30cm$ $S_{ABC} = \dfrac{1}{2}.AH.BC = \dfrac{1}{2}.30.(25 + 36) = 915 cm2$

Áp dụng Định lý Pythagoras cho 2 tam giác vuông ABH và ACH ta có:

$\begin{array}{l} A{B^2} = B{H^2} + A{H^2}\\ \Rightarrow A{B^2} = {25^2} + {30^2} = 1525\\ \Rightarrow AB \approx 39,05cm\\ A{C^2} = C{H^2} + A{H^2}\\ \Rightarrow A{C^2} = {36^2} + {30^2} = 2196\\ \Rightarrow AC \approx 46,86cm \end{array}$

Chu vi tam giác ABC là: P = AB + AC + BC= 39,05 + 46,86 + 61 = 146,91cm

Bài 3: Bóng của một ống khói nhà máy trên mặt đất có độ dài là 36,9m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 1,62m. Tính chiều cao của ống khói

Gợi ý đáp án

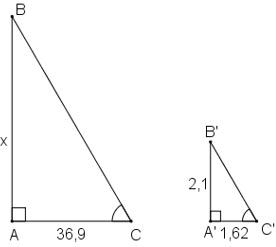
Giả sử thanh sắt là A'B', có bóng là A'C'.

Vì ống khói và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A'B'C' đều là tam giác vuông.

$\widehat {ACB} = \widehat {A'C'B'}$ $\Rightarrow$ $Khi \dfrac{AB}{A'B'} = \dfrac{AC}{A'C'}, ta suy ra$ $AB= \dfrac{A'B'.AC}{A'C'}, từ đó$ $AB= \dfrac{2,1.36,9}{1,62}, kết quả thu được là$ $AB ≈ 47,8m$

Bài 4: Trong tam giác vuông ABC vuông tại A, chân đường cao AH chia cạnh huyền BC thành hai phần, với BH = 4cm và HC = 9cm. Hãy tính diện tích của tam giác ABC?

A. S_ABC = 39cm²
B. S_ABC = 36cm²C. S_ABC = 78cm²
D. S_ABC = 18cm²

Áp dụng công thức diện tích trong tam giác ABC vuông tại A

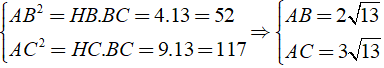
Vậy S_ABC = 1/2AB.AC = 1/2.2√(13) .3√(13) = 39( cm² )

Lựa chọn đáp án A.

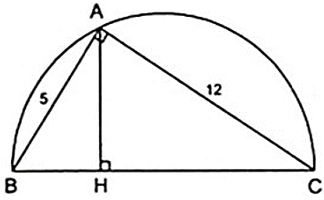
Bài 5: Cho hình bên là tam giác ABC vuông tại A, đường cao AH

a) Trong hình trên có bao nhiêu cặp tam giác đồng dạng với nhau. Hãy chỉ ra các cặp đồng dạng và theo các đỉnh tương ứng.

b) Cho biết AB = 5cm, AC = 12cm. Tính độ dài các đoạn thẳng BC, AH, BH và CH.

Hướng dẫn:

a) Trong hình trên có 3 cặp tam giác đồng dạng là BHA và BAC; CHA và CAB; HAB và HCA.

b) Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A ta có:

BC² = CA² + AB² ⇒ BC² = 12² + 5² = 13² ⇔ BC = 13 cm

Vì S_ABC = 1/2AB.AC = 1/2AH.BC ⇒ AH.BC = AB.AC

Hay 12.5 = AH.13 ⇒ AH = 60/13 cm

Từ phần a ta có: Δ BHA ∼ Δ BAC ⇒ BH/BA = BA/BC hay BH/5 = 5/13 ⇔ BH = 25/13 cm

Do đó: CH = BC - BH = 13 - 25/13 = 144/13 cm

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]