Hai tam giác tương tự khi các góc tương ứng của chúng bằng nhau và các cạnh tương ứng tỉ lệ với nhau. Vậy các trường hợp tương tự của tam giác là gì? Mời quý thầy cô cùng các bạn học sinh theo dõi bài viết dưới đây nhé.
Các trường hợp tương tự của tam giác được tổng hợp đầy đủ lý thuyết, đặc điểm, cách nhận biết và các dạng bài tập kèm theo. Qua đó giúp các bạn lớp 8 có thêm nhiều tư liệu tham khảo, trau dồi kiến thức để học tốt Toán 8.
1. Hai tam giác tương tự là gì?
Hai tam giác được gọi là tương tự khi các góc tương ứng của chúng bằng nhau và các cạnh tương ứng tỉ lệ với nhau.
2. Đặc điểm của hai tam giác đồng dạng
Đặc điểm hoán vị: Nếu tam giác A’B’C’ đồng dạng với tam giác ABC thì tam giác ABC cũng đồng dạng với tam giác A’B’C’
Đặc điểm thứ hai: Nếu tam giác A’B’C’ đồng dạng với tam giác A’’B’’C’’, tam giác A’’B’’C’’ đồng dạng với tam giác ABC thì chúng ta có cặp tam giác đồng dạng A’B’C’ và ABC
3. Các tình huống đồng dạng của tam giác
Dưới đây là cách nhận biết hai tam giác đồng dạng trong hình học.
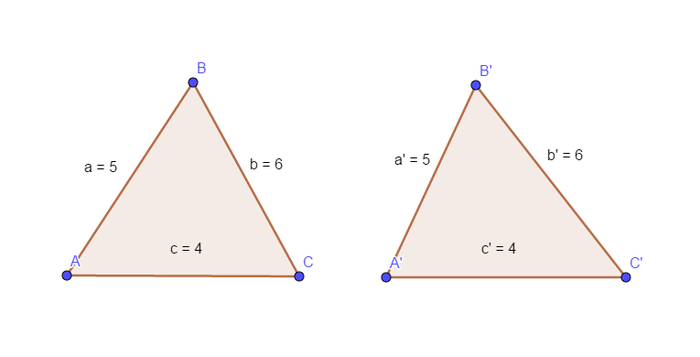
Tình huống 1: Cạnh- cạnh- cạnh
Trong tình huống này hai tam giác đồng dạng với nhau khi ba cạnh của tam giác này bằng ba cạnh của tam giác kia. Đối với tình huống này chúng ta sẽ không cần phải so sánh giá trị góc của hai tam giác với nhau.
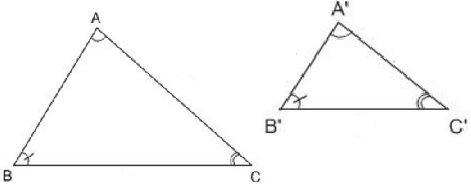
Tình huống 2: góc - góc
Hai tam giác được gọi là hai tam giác đồng dạng với nhau nếu một trong hai cặp góc và một cặp cạnh của chúng tương ứng bằng nhau.
Tình huống 3: góc - cạnh - góc
Trong tình huống góc - cạnh- góc này, hai tam giác được xem là hai tam giác đồng dạng với nhau khi hai góc và cạnh bên của cả hai tam giác đó bằng nhau.
Hoặc chúng ta có thể hiểu rằng, trường hợp này là hai tam giác đồng dạng khi hai cạnh có tỉ lệ bằng nhau và góc xen giữa hai cạnh của hai cạnh bằng nhau.
4. Bài tập chứng minh hai tam giác đồng dạng
Bài tập 1: Cho tam giác ABC có các cạnh tương ứng AB= 6cm, AC= 7cm và BC = 9cm. Tam giác A’B’C’ là một tam giác vuông tại A có A’B’= 12 cm, A’C’ = 14 cm. Hãy chứng minh hai tam giác trên đồng dạng với nhau.
Bài tập 2: Cho tam giác ABC có AB = 15 cm, AC = 20 cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD = 8cm, AE = 6cm. Chứng minh Δ AED ∼ Δ ABC.
Bài tập 3: Trên một cạnh của một góc xOy ( Ox ≠ Oy ) đặt các đoạn thẳng OA = 5cm, OB = 16cm Trên cạnh thứ hai của góc đó đặt các đoạn thẳng OC = 8cm, OD = 10cm.
a) Chứng minh Δ OCB ∼ Δ OAD
b) Gọi I là giao điểm của các cạnh AD và BC. Chứng minh rằng Δ IAB và Δ ICD có các góc bằng nhau từng đôi một
