Cách làm bài Advanced Math trong SAT Math, kèm theo ví dụ và bài tập luyện tập

Tổng quan về các dạng bài Advanced Math trong SAT Math

Cụ thể, yêu cầu của những câu hỏi thuộc phần này có thể xoay quanh việc chứng minh sự hiểu biết về giá trị tuyệt đối, phương trình bậc hai, hàm mũ, đa thức, phân thức, căn thức và các phương trình phi tuyến khác. Ngoài ra, phần này cũng đánh giá khả năng làm việc với hệ phương trình có hai biến và các hàm số phi tuyến.

Các đặc điểm nổi bật của phần Advanced Math

Thời gian làm bài và số lượng câu hỏi cần hoàn thành

Dạng bài Advanced Math chiếm tỉ lệ khoảng 35% trong tổng số câu hỏi của phần Toán, với số câu hỏi giao động từ 13-15 câu. Với thời gian làm bài Toán là 70 phút, thí sinh có thể xem xét phân bổ khoảng 25 phút cho dạng bài này.

Các loại câu hỏi trong phần Advanced Math

Theo hướng dẫn từ College Board, phần Advanced Math thường bao gồm các dạng câu hỏi sau:

• Biến đổi các biểu thức tương đương

• Giải phương trình phi tuyến với một biến

• Giải hệ phương trình với hai biến

• Vận dụng các

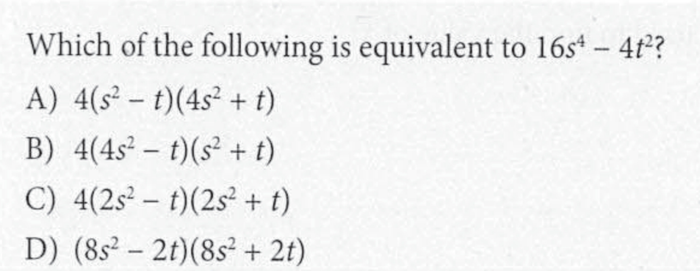
Các tiêu chí đánh giá quan trọng cần lưu ý

Nhìn chung, phần thi SAT Math sẽ đánh giá kiến thức toán học và khả năng vận dụng linh hoạt của thí sinh vào đa dạng chuyên đề nói chung và dạng Advanced Math nói riêng. Để hoàn thành tốt các câu hỏi dạng này, thí sinh có thể tham khảo để cải thiện những yếu tố dưới đây:

• Khả năng nắm bắt vấn đề: Trước khi bắt đầu giải bài toán, người học cần đảm bảo đã hiểu rõ yêu cầu của vấn đề. Đọc đề cẩn thận để xác định những thông tin quan trọng và mục tiêu của bài toán, đặc biệt là trong các bài toán liên quan đến phương trình phi tuyến và hàm số phi tuyến.

• Khả năng xác định thông tin chính xác: Tìm các thông tin được cung cấp trong đề bài và xác định những dữ liệu quan trọng cần thiết để giải quyết các phương trình phi tuyến và hệ phương trình.

• Khả năng phân tích và giải phương trình: Đối với các bài toán yêu cầu giải phương trình phi tuyến hoặc hệ phương trình, người học cần thực hiện các bước phân tích cẩn thận và chọn phương pháp giải phù hợp.

• Khả năng ứng dụng kiến thức với biểu thức: Đảm bảo người học nắm vững cách biến đổi và sử dụng các biểu thức đại số, đặc biệt là các biểu thức tương đương, để giải quyết các vấn đề phức tạp.

Phương pháp thực hiện dạng bài Advanced Math trong SAT Math

Bước 1: Phân tích đề bài và xác định yêu cầu cần giải quyết

Trước tiên, đọc kỹ đề bài để xác định những yêu cầu cụ thể của câu hỏi. Xác định loại phương trình hoặc biểu thức nào cần giải quyết (ví dụ: phương trình bậc hai, phương trình căn thức, phương trình đa thức, hệ phương trình, v.v.).

Nếu đề bài liên quan đến hàm số hoặc biểu đồ, hãy xác định dạng hàm số (bậc hai, đa thức, hàm mũ, v.v.) và những đặc điểm chính của đồ thị hoặc biểu thức đó (ví dụ: đỉnh của parabol, nghiệm của phương trình).

Bước 2: Xây dựng biểu thức hoặc phương trình cần thiết

Sau khi xác định yêu cầu đề bài, lập phương trình hoặc biểu thức cần giải dựa trên thông tin đã phân tích. Có thể sử dụng các công thức hoặc quy tắc đã học, như cộng, trừ, nhân, chia đa thức, hoặc áp dụng các bước rút gọn phương trình.

Trong trường hợp đề bài yêu cầu giải một hệ phương trình, hãy thiết lập các phương trình và kiểm tra xem có bao nhiêu biến cần giải.

Bước 3: Tiến hành giải phương trình hoặc biểu thức đã lập

Thực hiện các phép toán cần thiết để giải phương trình hoặc biểu thức. Có thể cần phải sử dụng phương pháp phân tích, đặt ẩn phụ, hoặc khai triển các đa thức.

Nếu đề bài yêu cầu xây dựng hoặc phân tích hàm số, hãy áp dụng các quy tắc về hàm số để giải quyết bài toán (ví dụ: tìm đạo hàm để xác định cực trị, sử dụng tính chất đối xứng của hàm bậc hai, v.v.).

Bước 4: Kiểm tra kết quả và so sánh với đề bài

Sau khi có đáp án, kiểm tra lại các bước giải để đảm bảo không có sai sót nào trong quá trình tính toán.

Đối chiếu kết quả với yêu cầu của đề bài để đảm bảo rằng đáp án đáp ứng đúng mục tiêu (ví dụ: nghiệm của phương trình, giá trị của hàm số, biểu thức đã rút gọn, v.v.).

Nếu cần, có thể thử lại với các giá trị cụ thể hoặc kiểm tra xem kết quả có phù hợp với ngữ cảnh của bài toán không.

Ví dụ áp dụng chiến lược 4 bước vào câu hỏi thực tế

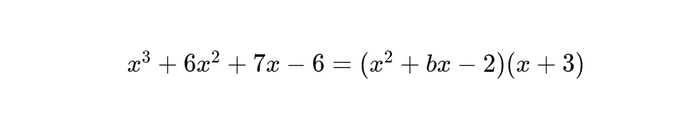
In the given equation, b is a constant. If the equation is true for all values of x, what is the value of b?

A) 2

B) 3

C) 7

D) 9

Bước 1: Phân tích đề bài và xác định yêu cầu

Đề bài yêu cầu xác định giá trị của b trong phương trình đa thức đã cho: x^3 + 6x^2 + 7x - 6 = (x^2 + bx - 2)(x + 3). Đây là một bài toán liên quan đến việc xác định hệ số trong một phương trình bậc ba.

Bước 2: Lập biểu thức hoặc phương trình

Để tìm b, bạn cần nhân hai biểu thức (x^2 + bx - 2) và (x + 3), rồi so sánh kết quả với phương trình đã cho để đối chiếu các hệ số của các số hạng có cùng bậc của x.

Bước 3: Giải phương trình hoặc biểu thức

Thực hiện phép nhân:

(x^2 + bx - 2)(x + 3) = x^3 + 3x^2 + bx^2 + 3bx - 2x - 6 = x^3 + (3 + b)x^2 + (3b - 2)x - 6

So sánh với phương trình đã cho: x^3 + 6x^2 + 7x - 6, ta có:

Hệ số của x^2: 3 + b = 6 ⇒ b = 3.

Bước 4: Kiểm tra kết quả và đối chiếu với đề bài

Sau khi tìm được b = 3, kiểm tra lại phép nhân và các hệ số đã đối chiếu để đảm bảo không có sai sót. Kết quả này khớp với yêu cầu của đề bài, do đó đáp án là B) 3.

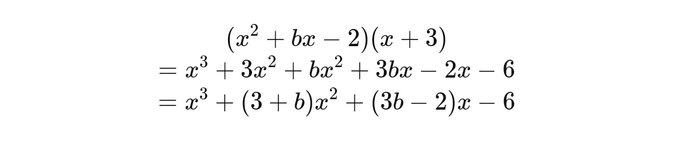
Câu hỏi 2: Giải phương trình một biến

A car is traveling at x feet per second. The driver sees a red light ahead, and after 1.5 seconds reaction time, the driver applies the brake. After the brake is applied, the car takes x/24 seconds to stop, during which time the average speed of the car is x/2 feet per second. If the car travels 165 feet from the time the driver saw the red light to the time it comes to a complete stop, which of the following equations can be used to find the value of x?

A) x^2 + 48x - 3960 = 0

B) x^2 + 48x - 7920 = 0

C) x^2 + 72x - 3960 = 0

D) x^2 + 72x - 7920 = 0

Bước 1: Phân tích đề bài và xác định yêu cầu

Đề bài cho: Một chiếc xe đang di chuyển với vận tốc x feet/s. Sau khi phanh, xe đi thêm một quãng đường và dừng lại.

Yêu cầu: Tìm phương trình để tính vận tốc ban đầu x của xe, biết tổng quãng đường xe đi được và thời gian phanh.

Bước 2: Lập phương trình hoặc biểu thức

Quãng đường đi được trong 1.5s đầu: 1.5x (feet)

Thời gian phanh: x/24 (s)

Quãng đường đi được trong khi phanh: (x/2) * (x/24) = x^2/48 (feet) (vì vận tốc trung bình trong quá trình phanh là x/2 feet/s)

Tổng quãng đường: 1.5x + x^2/48 = 165

Bước 3: Giải phương trình hoặc biểu thức

Quy đồng mẫu số: 48 * 1.5x + x^2 = 165 * 48

Rút gọn: 72x + x^2 = 7920

Đưa về dạng phương trình bậc hai: x^2 + 72x - 7920 = 0

Bước 4: Kiểm tra kết quả và đối chiếu với đề bài

Phương trình thu được là x^2 + 72x - 7920 = 0

So sánh với các đáp án: Đáp án đúng là D) x^2 + 72x - 7920 = 0

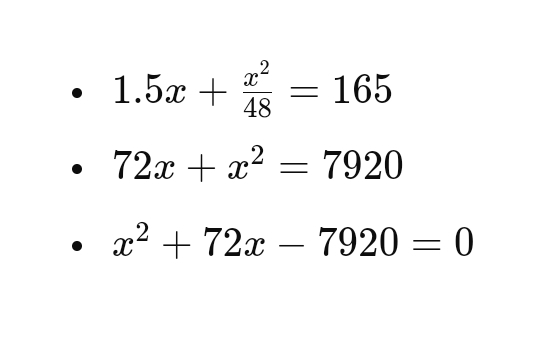
Câu hỏi 3:  Hàm số phi tuyến

The population of a city is increasing at a rate of 0.6% per year. The current population is 80,000 people. Choose the mathematical expression that describes the population of the city after t years:

A) 80,000(1 + 0.006)^t

B) 80,000 + 0.6t

C) 80,000 * 0.6^t

D) 80,000 / (1 + 0.006)^t

Bước 1: Phân tích đề bài và xác định yêu cầu

Đề bài cho: Dân số của một thành phố đang tăng với tốc độ 0.6% mỗi năm. Dân số hiện tại là 80,000 người.

Yêu cầu: Tìm biểu thức toán học mô tả dân số của thành phố sau t năm.

Bước 2: Lập biểu thức hoặc phương trình

Phân tích: Để tính dân số sau t năm, ta cần nhân dân số ban đầu với tỷ lệ tăng trưởng (1 + tỷ lệ tăng trưởng) lũy thừa t.

Biểu thức: Dân số sau t năm = Dân số ban đầu * (1 + Tỷ lệ tăng trưởng)^t

Áp dụng vào bài toán:

Dân số ban đầu = 80,000

Tỷ lệ tăng trưởng = 0.6% = 0.006

Biểu thức: 80,000 * (1 + 0.006)^t = 80,000 * (1.006)^t

Bước 3: Giải phương trình hoặc biểu thức

Trong trường hợp này, chúng ta không cần giải phương trình mà chỉ cần xây dựng biểu thức.

Biểu thức cuối cùng: 80,000 * (1.006)^t

Bước 4: Kiểm tra kết quả và đối chiếu với đề bài

Kiểm tra: Biểu thức ta tìm được hoàn toàn phù hợp với công thức tính lãi kép, thường được sử dụng trong các bài toán liên quan đến tăng trưởng dân số, lãi suất,...

Đối chiếu: Biểu thức này cho ta biết dân số của thành phố sau t năm, bắt đầu từ dân số ban đầu là 80,000 và tăng 0.6% mỗi năm. Vậy đáp án đúng là: A) 80,000(1 + 0.006)^t

Thực hành

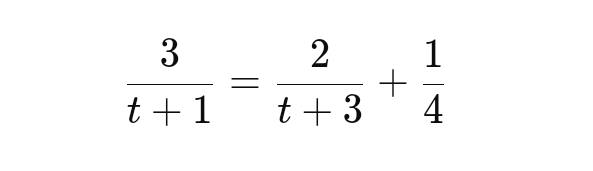
If t is a solution to the given equation and t > 0, what is the value of t?

A) 0

B) 5

C) 10

D) 15

Câu hỏi luyện tập 2:

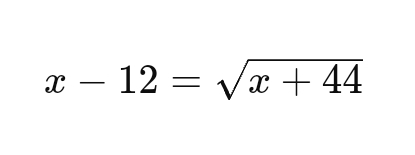
What are all possible solutions to the given equation?

A) 5

B) 20

C) -5 and 20

D) 5 and 20

Câu hỏi luyện tập 3:

For a certain reservoir, the function f gives the water level fn), to the nearest whole percent of capacity, on the nth day of 2016. Which of the following is the best interpretation of f(37) = 70?

A) The water level of the reservoir was at 37% capacity for 70 days in 2016

B) The water level of the reservoir was at 70% capacity for 37 days in 2016.

C) On the 37th day of 2016, the water level of the reservoir was at 70% capacity.

D) On the 70th day of 2016, the water level of the reservoir was at 37% capacity

Đáp án:

Câu hỏi 1: Đáp án B

Câu hỏi 2: Đáp án B

Câu hỏi 3: Đáp án C

Tóm tắt