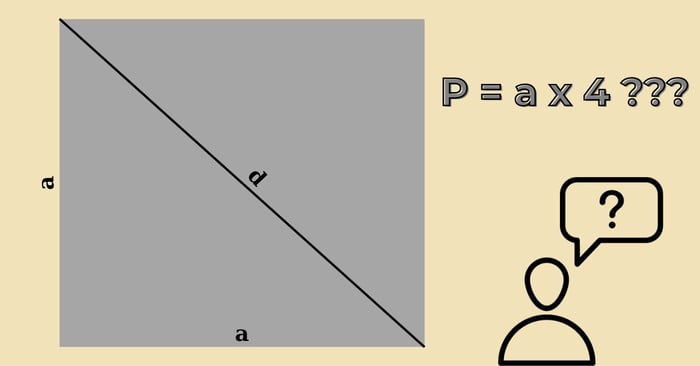
Công thức tính chu vi và đường chéo của hình vuông không chỉ là kiến thức cơ bản mà còn là kỹ năng quan trọng được áp dụng rộng rãi trong nhiều lĩnh vực. Việc hiểu rõ những công thức này giúp bạn có nền tảng kiến thức vững chắc và có thể áp dụng linh hoạt khi cần thiết. Dưới đây là cách chi tiết để tính chu vi hình vuông và đường chéo, được tổng hợp từ Mytour để bạn tham khảo.
Chu vi hình vuông là gì?
Để tính chu vi hình vuông, trước tiên bạn cần hiểu rõ về định nghĩa và bản chất của hình vuông. Dưới đây là những thông tin cơ bản để bạn tiếp cận với cách tính này một cách dễ dàng.
Định nghĩa cơ bản về chu vi hình vuông
Chu vi của hình vuông là tổng chiều dài của các cạnh của hình. Với hình vuông, mỗi cạnh đều bằng nhau nên công thức tính chu vi là chiều dài cạnh nhân 4, được đo bằng đơn vị chiều dài như centimet hoặc mét.
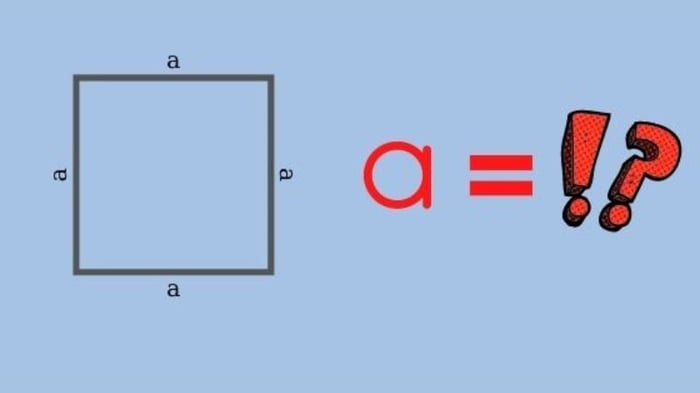
Công thức và cách tính chu vi hình vuông cơ bản
Công thức tính chu vi hình vuông được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau, đặc biệt là trong môn toán. Đây là những kiến thức cơ bản mà mọi học sinh cần nắm để giải quyết các bài toán phức tạp hơn.
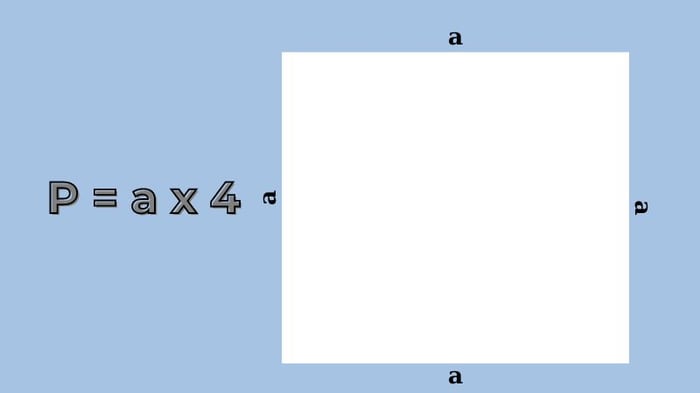
Công thức tính chi tiết chu vi hình vuông bạn có thể tham khảo như sau:
Chu vi = Chiều dài cạnh x Số cạnh
Theo đó:
- Chu vi là tổng chiều dài của các cạnh của hình vuông.
- Chiều dài cạnh là độ dài của từng cạnh của hình vuông, thường ký hiệu là a.
- Số cạnh là số lượng cạnh của hình vuông và mỗi hình vuông có 4 cạnh.
Ví dụ minh họa: Giả sử chúng ta có một hình vuông có cạnh dài a = 5 cm. Để tính chu vi của hình vuông này, áp dụng công thức như sau:
Chu vi = Chiều dài cạnh x Số cạnh = 5 x 4 = 20 cm.
Chú thích: Vì mỗi cạnh của hình vuông đều có cùng độ dài và hình vuông có 4 cạnh, nên chu vi của hình vuông này là 20 cm. Đây là một ví dụ minh họa về cách tính chu vi hình vuông dựa trên công thức cơ bản. Bạn có thể áp dụng công thức và cách tính chu vi hình vuông này cho các hình vuông khác trong các bài toán khác.
Những lưu ý khi tính chu vi hình vuông
Quá trình áp dụng công thức tính chu vi hình vuông dường như đơn giản nhưng thực tế lại có thể phức tạp và dẫn đến sai sót nếu bạn không chính xác trong việc xác định hoặc tính toán các thông số. Để tránh điều này, hãy lưu ý một số điều sau đây.
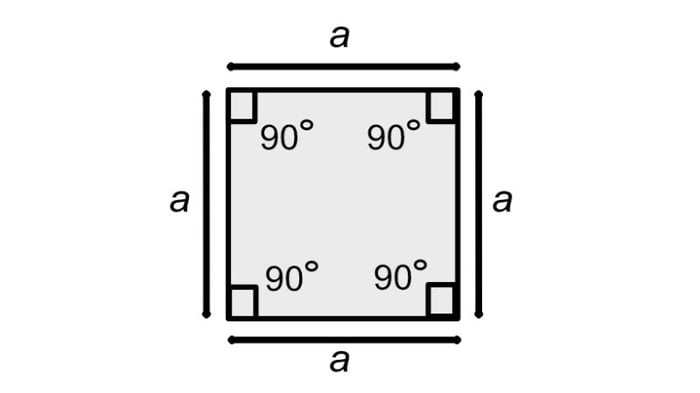
- Trong các bài thi có nhiều hình vuông, cần xác định chính xác độ dài cạnh hình vuông để tính toán. Đồng thời, phải đảm bảo đã đo đúng độ dài cạnh bằng các công cụ đo như thước đo hoặc rè.
- Khi tính toán, tránh làm tròn quá nhiều số, đặc biệt là khi đo trong các đơn vị nhỏ như milimet. Số liệu sai có thể ảnh hưởng đến kết quả của các câu hỏi khác trong đề thi.
- Nên sử dụng các công cụ hỗ trợ như máy tính hoặc ứng dụng tính toán để giảm thiểu sai số. Cần so sánh đáp án với số liệu đã đo để kiểm tra tính chính xác.
- Hãy xác định rõ đơn vị đo và đảm bảo cả chiều dài cạnh và kết quả chu vi đều sử dụng cùng một đơn vị. Đây là lỗi phổ biến của học sinh trong các đề thi. Vì vậy, hãy kiểm tra kỹ trước khi đưa ra kết quả cuối cùng.
Ứng dụng của cách tính chu vi hình vuông trong thực tế
Cách tính chu vi hình vuông có nhiều ứng dụng thực tế trong nhiều lĩnh vực khác nhau. Dưới đây là một số ví dụ về cách áp dụng kiến thức về chu vi hình vuông bạn không thể bỏ qua.

- Chu vi của hình vuông là phần cơ bản trong giáo trình hình học và toán học, giúp học sinh hiểu về mối liên hệ giữa chu vi, diện tích và độ dài cạnh.
- Trong ngành xây dựng, chu vi hình vuông được sử dụng để tính toán lượng vật liệu cần thiết cho việc xây dựng các công trình như tường, sàn nhà hoặc cấu trúc khác.
- Chu vi hình vuông còn được áp dụng để tính diện tích khi kết hợp với chiều rộng hoặc chiều dài. Đây là công cụ hữu ích trong quản lý và đo lường diện tích đất, đặc biệt là trong dự án bất động sản.
- Trong thiết kế đồ họa, kiến thức về cách tính chu vi hình vuông là cơ sở để xác định kích thước và tỷ lệ của các đối tượng, đóng vai trò quan trọng trong việc tạo ra các bản vẽ kỹ thuật và đồ họa chất lượng cao.
Đường chéo của hình vuông là gì?
Tương tự như cách tính chu vi hình vuông, để tính toán đường chéo của hình vuông, bạn cần hiểu rõ các định nghĩa và lý thuyết cơ bản liên quan.
Định nghĩa cơ bản về đường chéo của hình vuông
Đường chéo (d) của hình vuông là đường thẳng nối hai đỉnh đối diện. Trong không gian hình học, đường chéo chia hình vuông thành hai tam giác vuông đều và tạo góc 45 độ với mỗi cạnh của hình vuông. Đây là đặc điểm đặc trưng của hình vuông.
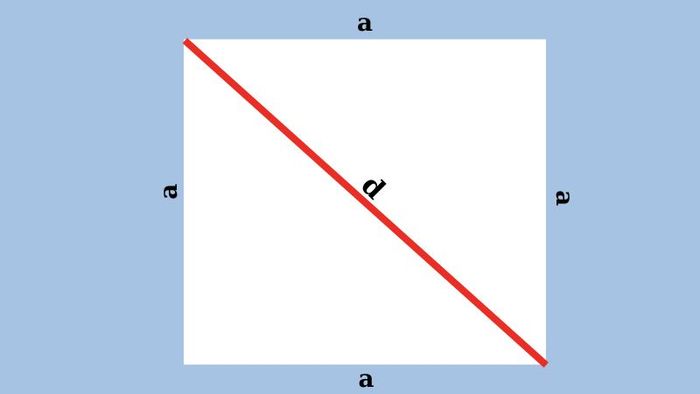
Trong các bài toán, độ dài đường chéo là yếu tố quan trọng trong việc tính toán chu vi hình vuông. Để tính độ dài cạnh của hình học, bạn cần biết độ dài của đường chéo. Điều này đặc biệt quan trọng trong các lĩnh vực như đo đạc, xây dựng và thiết kế, giúp tối ưu hóa thời gian thực hiện.
Công thức tính đường chéo hình vuông và ứng dụng
Để tính độ dài đường chéo (d) của hình vuông, bạn có thể sử dụng công thức Pythagoras. Đây là đường chéo tạo thành hai tam giác vuông. Cụ thể, công thức tính toán như sau:
d² = a² + b²
Trong đó:
- d là chiều dài của đường chéo.
- a và b là chiều dài của hai cạnh liền kề của hình vuông. Thông thường, hai cạnh này bằng nhau.
Ví dụ minh họa: Giả sử chúng ta có một hình vuông có cạnh dài 6 cm. Hãy tính độ dài đường chéo và chu vi của hình vuông.
Lời giải:
Áp dụng công thức Pythagoras, ta tính được độ dài của đường chéo như sau:
d² = a² + b²= 6² + 6² = √72 = 8,49 cm
Do đó, cách tính chu vi hình vuông sẽ được thực hiện như sau:
Chu vi = Độ dài cạnh x Số cạnh = 6 x 4 = 24 cm.
Lưu ý: Cách tính đường chéo và chu vi hình vuông có những điều lưu ý tương tự nhau. Bạn có thể tham khảo các lưu ý khi tính chu vi hình vuông để quá trình tính toán diễn ra chính xác và nhanh chóng hơn.
Ứng dụng của đường chéo hình vuông trong thực tế
Cách tính đường chéo của hình vuông có nhiều ứng dụng thực tiễn, đặc biệt là trong các lĩnh vực như đo đạc, xây dựng và thiết kế. Dưới đây là một số ví dụ về cách áp dụng đường chéo hình vuông trong thực tế mà bạn có thể tham khảo.

- Trong ngành xây dựng, tính đường chéo hình vuông được áp dụng để xác định chiều dài của đường chéo giữa các khu vực vuông góc. Ví dụ như khi xây dựng một tường chéo giữa hai tường vuông góc. Ngoài ra, đường chéo cũng hữu ích trong tính chu vi hình vuông và đo đạc khu đất, kích thước các phòng và diện tích hình vuông.
- Trong lĩnh vực thiết kế nội thất, đường chéo hình vuông thường được sử dụng để tạo ra các đường chéo trong bố cục nội thất. Điều này giúp tăng tính cân đối và thẩm mỹ cho các sản phẩm nội thất.
- Ngoài ra, trong hình học và hình học không gian, công thức tính đường chéo hình vuông được sử dụng rộng rãi để giải quyết các vấn đề liên quan đến kích thước và vị trí của các hình vuông, giúp giải quyết các bài toán hình học một cách nhanh chóng.
Tóm lại
Đó là cách tính chu vi hình vuông và đường chéo của chúng mà bạn có thể tham khảo và áp dụng ngay trên các bài tập của bạn. Qua bài viết này, Mytour hi vọng các bạn đọc sẽ nắm được cách tính cơ bản được giới thiệu ở trên và có thể cải thiện vị trí và thành tích học tập của mình.
