Cách tính thể tích hình hộp chữ nhật

Buzz

Nội dung bài viết

Thể tích của hình hộp chữ nhật

1. Ý nghĩa của hình hộp chữ nhật

2. Cách tính thể tích hình hộp chữ nhật

3. Diện tích của hình hộp chữ nhật

4. Cách tính thể tích hình hộp chữ nhật

5. Ví dụ tính thể tích khối hộp chữ nhật

6. Bài tập trắc nghiệm về thể tích khối hộp chữ nhật

7. Bài tập tính diện tích và thể tích hình hộp chữ nhật

Xem thêm

Đọc tóm tắt

- Thể tích hình hộp chữ nhật là kiến thức cơ bản trong chương trình Toán lớp 8 và lớp 9, thường xuất hiện trong các bài thi vào lớp 10. Công thức tính thể tích hình hộp chữ nhật là tích của chiều dài, chiều rộng và chiều cao (V = a x b x h). Hình hộp chữ nhật có 6 mặt, 8 đỉnh và 12 cạnh, với hai mặt đối diện là mặt đáy và 4 mặt còn lại là mặt bên.
- Để tính thể tích, cần xác định các kích thước và áp dụng công thức V = a x b x h.
- Các bài tập và ví dụ minh họa bao gồm tính thể tích, diện tích mặt ngoài, và diện tích toàn phần của hình hộp chữ nhật, cùng với bài tập trắc nghiệm để kiểm tra kiến thức.
- Các bài toán liên quan đến phòng hình hộp chữ nhật bao gồm tính chi phí sơn với giá 50.000 đồng/m², số viên gạch lát nền 20cm cho phòng 4m x 3m, diện tích toàn phần phòng, chi phí sơn bốn bức tường phòng 10m x 5m x 4m (25.000 đồng/m²) với cửa ra vào và cửa sổ, và kiểm tra xem nước trong thùng hình hộp chữ nhật cao 1m, dài 50cm, rộng 50cm có tràn ra ngoài khi chứa 50% thể tích nước và 50 viên gạch không.

Thể tích hình hộp chữ nhật là một trong những kiến thức căn bản trong chương trình Toán lớp 8, lớp 9 và thường xuất hiện trong các bài thi vào lớp 10.

Công thức tính thể tích hình hộp chữ nhật tổng hợp toàn bộ kiến thức về khái niệm, công thức tính, ví dụ minh họa kèm theo các dạng bài tập tự luyện. Qua đó giúp các bạn học sinh tham khảo, hệ thống lại kiến thức để giải nhanh các bài tập về tính thể tích hình chữ nhật. Ngoài ra để nâng cao kiến thức môn Toán thật tốt các em xem thêm một số tài liệu như: công thức tính diện tích tam giác.

Thể tích của hình hộp chữ nhật

1. Hình hộp chữ nhật là gì?
2. Công thức tính thể tích hình hộp chữ nhật
3. Diện tích hình hộp chữ nhật
4. Các bước tính thể tích hình hộp chữ nhật
5. Ví dụ tính thể tích khối hộp chữ nhật
6. Bài tập trắc nghiệm thể tích khối hộp chữ nhật
7. Bài tập tính diện tích và thể tích hình hộp chữ nhật

1. Ý nghĩa của hình hộp chữ nhật

Hình hộp chữ nhật là một dạng hình trong không gian ba chiều, trong đó mỗi mặt là một hình chữ nhật. Hình hộp chữ nhật có tổng cộng 6 mặt, 8 đỉnh và 12 cạnh. Nếu hai mặt đối diện được gọi là mặt đáy, thì 4 mặt còn lại là các mặt bên của hình hộp chữ nhật.

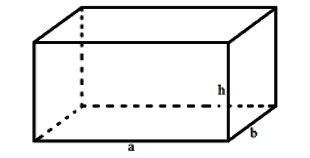
2. Cách tính thể tích hình hộp chữ nhật

Thể tích của hình hộp chữ nhật bằng tích của chiều dài nhân chiều rộng nhân chiều cao của hình.

Thể tích của hình hộp chữ nhật là khối lượng không gian mà hình chiếm, được tính bằng tích của diện tích đáy và chiều cao:

Thể tích = a x b x h

Nơi đó:

Thể tích là khối lượng không gian của hình hộp chữ nhật.
a là chiều dài của hình hộp chữ nhật.
b là chiều rộng của hình hộp chữ nhật.
h là chiều cao của hình hộp chữ nhật.

3. Diện tích của hình hộp chữ nhật

- Diện tích bề mặt của hình hộp chữ nhật:

${{S}_{xq}}=2h.(a+b)$

- Tổng diện tích của hình hộp chữ nhật:

${{S}_{tp}}={{S}_{2d}}+{{S}_{xq}}=2ab+2h.(a+b)$

Nơi đó:

S là diện tích xung quanh hình hộp chữ nhật
a là chiều dài của hình hộp chữ nhật.
b là chiều rộng của hình hộp chữ nhật.
h là chiều cao của hình hộp chữ nhật.

$R=\frac{\sqrt{{{a}^{2}}+{{b}^{2}}+{{h}^{2}}}}{2}$

4. Cách tính thể tích hình hộp chữ nhật

Phương pháp 1

Để tính thể tích của một hình hộp chữ nhật bất kỳ, bạn cần xác định các biến trong công thức tính. Ví dụ, nếu bạn muốn tính thể tích nước của một hồ chứa nước hình hộp chữ nhật, bạn cần thực hiện các bước sau:

Ứng Dụng: Tính thể tích nước có thể chứa trong hồ nước (trong hình)

a. Xác Định Chiều Dài của Hình Hộp Chữ Nhật

Chiều dài là cạnh dài nhất của mặt phẳng hình chữ nhật nằm phía trên hoặc phía dưới của hình hộp chữ nhật. Bạn có thể sử dụng thước dây để đo cạnh dài nhất của mặt nước, ví dụ: chiều dài = 5 m.

b. Xác Định Chiều Rộng của Hình Hộp Chữ Nhật

Chiều rộng là cạnh ngắn nhất của mặt phẳng hình chữ nhật nằm bên trên hoặc bên dưới của hình hộp chữ nhật. Bạn có thể sử dụng thước dây để đo cạnh ngắn nhất của mặt nước, ví dụ: chiều rộng = 3 m.

c. Xác Định Chiều Cao của Hình Hộp Chữ Nhật

Chiều cao là cạnh đứng vuông góc với chiều dài và chiều rộng của hình hợp chữ nhật. Bạn có thể đo chiều cao của mặt nước bằng thước dây, ví dụ: chiều cao = 1,5 m.

d. Tính Tích Số của Ba Đơn Vị Chiều Dài, Chiều Rộng và Chiều Cao.

Bạn có thể nhân 3 đại lượng chiều rộng, chiều dài và chiều cao tùy ý, không cần quan tâm đến thứ tự trước, sau. Áp dụng công thức tính thể tích hình hộp chữ nhật cho hồ nước trên, ta có:

V = a.b.h = 5 (m) x 3 (m) x 1,5 (m) = 22,5 (m³)

Kết luận: Hồ nước có thể chứa được thể tích nước là 22,5 (m³).

Cách 2

Công thức tính thể tích hình hộp chữ nhật là V = a x b x c. Do đó, để tính được thể tích của hình hộp chữ nhật bất kì thì bạn cần phải xác định được các cạnh của hình hộp:

- Xác định được chiều dài hình hộp chữ nhật: Chiều dài chính là cạnh dài nhất của hình chữ nhật nằm ở mặt trên hoặc mặt dưới hình hộp chữ nhật.

- Xác định được chiều rộng của hình hộp chữ nhật: Chiều rộng này chính là cạnh ngắn nhất của hình chữ nhật mà bạn vừa xác định chiều dài ở trên.

- Xác định được chiều cao của hình hộp chữ nhật: Chiều cao là khoảng cách giữa 2 mặt đáy hay vuông góc với chiều dài và chiều rộng mà bạn vừa đo.

5. Ví dụ tính thể tích khối hộp chữ nhật

Bài 1: Hình hộp chữ nhật có chiều dài 8 m, chiều rộng 5 m và chiều cao 6 m. Tính đường chéo của hình hộp chữ nhật.

Giải:

$\sqrt{8^2\ +\ 6^2\ +\ 5^2}=\ 11,8m$

Bài 2:

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có chiều dài cạnh đáy là 7 cm, chiều rộng cạnh đáy là 3 cm, chiều cao cạnh đáy là 6 cm. Tính thể tích hình hộp chữ nhật ABCD.A’B’C’D’.

Lời giải:

Công thức tính thể tích hình hộp chữ nhật là V = abh

Thể tích của hình hộp chữ nhật ABCD.A’B’C’D’ là: V = 7.3.6 = 126 cm³

Bài 3: Một hồ chứa nước có dạng hình hộp chữ nhật có thể tích là 3000 m3, chiều rộng là 10 m và chiều cao của hồ là 12 m. Tính chiều dài của hồ.

Giải:

Chiều dài của hồ chứa nước là:

$a=\frac{V}{bh}\ =\ \frac{3000}{10.12}=25(m)$

Bài 4: Cho hình hộp chữ nhật với chiều dài là 2,5cm, chiều rộng là 1,8 cm và chiều cao là 2cm. Hãy tính thể tích, diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật đó đó.

Giải:

Theo yêu cầu, a = 2,5; b = 1,8 và h = 2. Áp dụng các công thức tính, ta có:

Thể tích của hình hộp chữ nhật là:

V = 2,5 * 1,8 * 2 = 9 (cm³)

Diện tích xung quanh của hình hộp chữ nhật là:

S_xq= 2.2.(2,5 + 1,8) = 17,2 (cm²)

Diện tích toàn bộ của hình hộp chữ nhật là:

S_tp = S_xq + 2ab = 17,2 + 2.2,5.1,8 = 26,2 (cm²)

Bài 5: Cho hình hộp chữ nhật ABCD.A'B'C'D' với các cạnh AB = 3cm, AD = 5cm, AA' = 4cm. Tính thể tích của hình hộp chữ nhật.

Đáp án:

Hình hộp chữ nhật ABCD.A'B'C'D' có kích thước chiều dài là 5 cm, chiều rộng là 3 cm và chiều cao là 4 cm.

Thể tích của hình hộp chữ nhật là: V = 5.3.4 = 60 (cm³).

Bài 6 Một khay nhựa dạng hình hộp chữ nhật được sử dụng để làm đá có kích thước đáy là 20 cm x 5 cm và chiều cao là 5 cm. Hãy tính dung tích nước tối đa có thể đổ vào khay.

Đáp án gợi ý:

Dung tích nước tối đa có thể đổ vào khay chính là thể tích của khay đó.

Ta tính được: V = 20.5.5 = 500 ^(cm3).

6. Bài tập trắc nghiệm về thể tích khối hộp chữ nhật

Câu 1: Cho một hình lập phương có diện tích của một mặt bên là 36cm². Hãy tính thể tích của hình lập phương?

A. 216cm ³

B. 144cm ³

C. 125cm ³

D.108cm ³

Câu 2: Diện tích toàn phần của một hình lập phương là 294 cm². Hãy tính thể tích của nó?

A. 300cm ³

B. 343 cm ³

C. 280cm ³

D. 320 cm ³

Câu 3: Cho một hình hộp chữ nhật ABCD.A'B'C'D'. Chọn câu phát biểu nào sau đây là đúng?

A. CC' ⊥ (AA'B'B)

B. A'D' ⊥ (BCC'B')

C. DC ⊥ (ADD'A')

D. CD ⊥ (A'B'C'D')

Câu 4: Trong hình hộp chữ nhật ABCD. MNPQ, với AB = 6cm; BC = 8cm và thể tích của hình hộp là 240cm³, hãy tính AA’

A. 5cm

B. 6cm

C. 8cm

D. 10cm

Câu 5: Cho một hình lập phương có thể tích là: 64cm³. Hãy tính diện tích của một mặt của hình lập phương?

A. 16cm ²

B. 8cm ²

C. 12cm ²

D. 64cm ²

Câu 6: Trong một hình lập phương có các cạnh có độ dài là 5cm. Thể tích của hình lập phương đó là bao nhiêu?

A. 100 cm ³

B.125/3 cm ³

C. 125 cm ³

D. 115 cm ³

Câu 7: Trong hình hộp chữ nhật ABCD.A'B'C'D', chọn phát biểu đúng trong các phát biểu sau:

A. ( ABCD ) ⊥ ( A'B'C'D' )	B. ( ADD'A' ) ⊥ ( BCC'B' )
C. ( ABB'A' ) ⊥ ( BCC'B' )	D. ( ABB'A' ) ⊥ ( CDD'C' )

Câu 8: Trong hình hộp chữ nhật ABCD. MNPQ, với AB = 6cm; BC = 8cm và thể tích của hình hộp là 240cm³, hãy tính AA’.

A. 5cm

B. 6cm

C. 8cm

D. 10cm

Câu 9: Trong hình hộp chữ nhật ABCD.A'B'C'D', với diện tích đáy SABCD = 24cm² và thể tích V = 84 cm³, chiều cao của hình hộp chữ nhật là bao nhiêu?

A. h = 5cm

B. h = 3,5cm

C. h = 4cm

D. h = 2cm

Câu 10: Hãy tính thể tích của khối hộp ABCD.A'B'C'D', biết rằng AA'B'D' là một khối tứ diện đều cạnh a.

Câu 11: Một người muốn sơn mặt ngoài của một cái thùng sắt không nắp dạng hình lập phương có cạnh 0,8m. Biết giá tiền mỗi mét vuông là 15000 đồng. Người đó sẽ phải trả bao nhiêu tiền?

A. 48000 đồng

B. 64000 đồng

C. 45000 đồng

D. 96000 đồng

Câu 12: Hãy chọn câu đúng. Trong hình hộp chữ nhật có ba kích thước lần lượt là: a, a, 2a, thể tích của hình hộp chữ nhật đó là gì?

A. a²

B. 2a³

C. 2a⁴

D. a³

Câu 13: Một hồ cá dạng hình hộp chữ nhật bằng kính (không nắp) có chiều dài 1 m, chiều rộng 70 cm, chiều cao 60 cm. Mực nước trong hồ cao 30 cm. Sau khi thêm một hòn đá vào hồ, thể tích nước tăng thêm 14000 cm³. Hỏi mực nước trong hồ lúc này cao bao nhiêu?

A. 40 cm

B. 30 cm

C. 32 cm

D. 35 cm

Câu 14: Một hồ cá dạng hình hộp chữ nhật bằng kính (không nắp) có chiều dài 80 cm, chiều rộng 50 cm. Mực nước trong hồ cao 35 cm. Sau khi thêm một hòn đá vào hồ, thể tích nước tăng thêm 20000 cm³. Hỏi mực nước trong hồ úc này cao bao nhiêu?

A. 40 cm

B. 30 cm

C. 60 cm

D. 50 cm

7. Bài tập tính diện tích và thể tích hình hộp chữ nhật

Bài 1: Cho một phòng có dạng hình hộp chữ nhật. Biết chiều dài và chiều rộng của phòng lần lượt là 3m và 2m và mặt bên chứa cạnh 3m có đường chéo dài 5m.

a) Tính diện tích mặt sàn của phòng.

b) Để sơn xung quanh phòng cần trả bao nhiêu tiền công cho thợ sơn biết giá công sơn là 50 000 đồng cho mỗi mét vuông.

Bài 2: Cho một phòng có dạng hình hộp chữ nhật. Chiều dài và chiều rộng phòng lần lượt là 4m và 3m, Mặt bên chứa cạnh 3m có đường chéo dài 5m.

a) Để lát nền gạch phòng cần ít nhất bao nhiêu viên gạch hoa hình vuông, biết mỗi viên gạch có số đo là 20cm

b) Tính diện tích toàn phần phòng.

Bài 3: Một phòng học hình hộp chữ nhật có chiều dài 10m, chiều rộng 5m và chiều cao 4m. Người ta định sơn bốn bức tường phòng, biết giá công tiền sơn là 25 000 đồng cho mỗi mét vuông. Hỏi chi phí tiền công là bao nhiêu? Biết phòng có một cửa chính cao 1,8m và chiều rộng 2m và hai cửa số có cùng chiều dài 80cm, chiều cao 60cm.

Bài 4: Một chiếc thùng có dạng hình hộp chữ nhật, cao 1m, dài 50cm và rộng 50cm. Các thợ xây đổ một lượng nước bằng 50% thể tích của thùng rồi thả vào đó 50 viên gạch hình hộp chữ nhật, mỗi viên có các kích thước cao, dài, rộng lần lượt là 10cm, 20cm, 15cm. Hỏi nước trong thùng có tràn ra ngoài không? Tại sao?

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]

Các câu hỏi thường gặp

Hình hộp chữ nhật là gì và có đặc điểm nào?

Hình hộp chữ nhật là một hình khối ba chiều có tất cả các mặt là hình chữ nhật. Hình này có 6 mặt, 8 đỉnh, và 12 cạnh, với 2 mặt đối diện là mặt đáy và các mặt còn lại là mặt bên.

Công thức tính thể tích của hình hộp chữ nhật là gì?

Công thức tính thể tích của hình hộp chữ nhật là V = a × b × h, trong đó a là chiều dài, b là chiều rộng và h là chiều cao của hình hộp chữ nhật.

Làm thế nào để tính thể tích của hình hộp chữ nhật trong thực tế?

Để tính thể tích của hình hộp chữ nhật, bạn chỉ cần xác định chiều dài, chiều rộng và chiều cao của hình, sau đó áp dụng công thức V = a × b × h để tính toán.

Thể tích của hồ chứa nước hình hộp chữ nhật có thể được tính như thế nào?

Để tính thể tích hồ chứa nước hình hộp chữ nhật, bạn cần đo chiều dài, chiều rộng và chiều cao của hồ. Sau đó nhân ba giá trị này lại với nhau theo công thức V = a × b × h.

Các bước tính thể tích hình hộp chữ nhật là gì?

Các bước tính thể tích hình hộp chữ nhật bao gồm: 1) Xác định chiều dài, chiều rộng và chiều cao của hình. 2) Áp dụng công thức V = a × b × h. 3) Tính tích của ba đại lượng để ra kết quả.

Tính thể tích hình hộp chữ nhật với các kích thước cụ thể như thế nào?

Ví dụ, nếu chiều dài là 5m, chiều rộng là 3m và chiều cao là 1.5m, thể tích sẽ được tính là V = 5 × 3 × 1.5 = 22.5m³.

Làm thế nào để tính diện tích toàn phần của hình hộp chữ nhật?

Diện tích toàn phần của hình hộp chữ nhật được tính bằng công thức: S = 2ab + 2ah + 2bh, trong đó a, b, h là chiều dài, chiều rộng và chiều cao của hình.

Các bài tập trắc nghiệm về thể tích hình hộp chữ nhật thường gặp là gì?

Các bài tập trắc nghiệm về thể tích hình hộp chữ nhật thường yêu cầu tính thể tích, diện tích hoặc các đặc tính khác của hình hộp chữ nhật dựa trên các kích thước cho trước.