Thể tích của khối lăng trụ là một trong những bài toán hình học không gian thú vị. Biết cách tính thể tích của khối lăng trụ giúp học sinh giải quyết bài tập và áp dụng vào thực tế. Vậy cách tính thể tích của khối lăng trụ như thế nào? Mời bạn đọc theo dõi bài viết dưới đây để biết thông tin chi tiết!
Định nghĩa
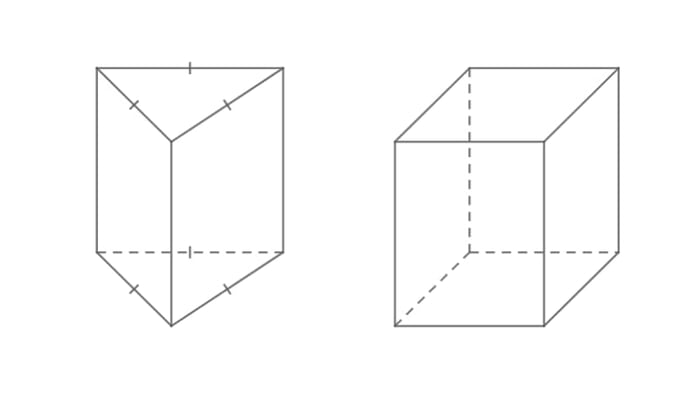
Khối lăng trụ, hay hình lăng trụ, là một trong những hình thể phổ biến trong cuộc sống. Hình lăng trụ có nhiều loại như lăng trụ đứng, lăng trụ đều, lăng trụ tam giác đều và các dạng khác. Dưới đây là định nghĩa và tính chất của từng loại hình lăng trụ để bạn có thêm kiến thức.
Hình lăng trụ
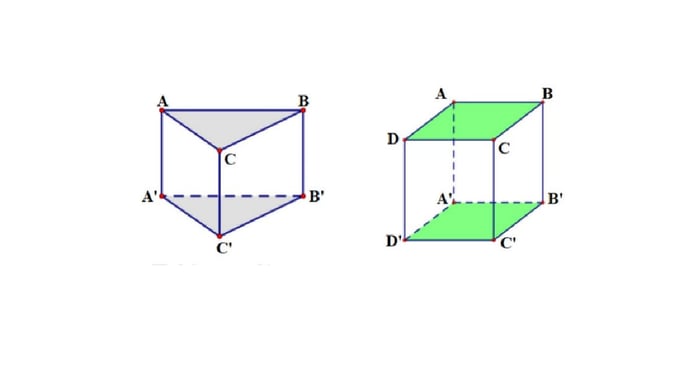
Hình lăng trụ là một hình đa diện có hai đáy nằm trên hai mặt phẳng song song và có hình đa giác bằng nhau. Đáy của hình lăng trụ có thể là hình chữ nhật, hình vuông, hình bình hành, tam giác,... Các mặt bên của hình lăng trụ là các hình bình hành, có các cạnh bằng nhau và song song.
Sau khi hiểu định nghĩa, bạn cần nắm các tính chất của hình lăng trụ để áp dụng vào giải các bài tập một cách linh hoạt. Các tính chất của hình lăng trụ bao gồm:
- Hai đáy của hình lăng trụ là hai đa giác bằng nhau nằm trong hai mặt phẳng song song.
- Các cạnh bên của hình lăng trụ song song với nhau.
- Các mặt bên của hình lăng trụ đều là hình bình hành.
Hình lăng trụ đứng
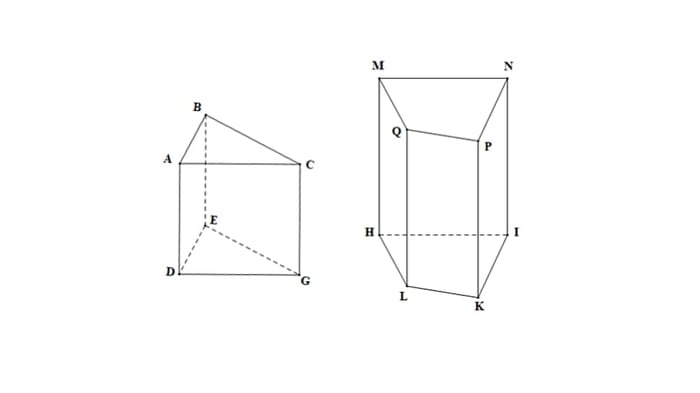
Khi nghiên cứu về thể tích của khối lăng trụ, chúng ta thực chất đang tính thể tích của hình lăng trụ đứng. Hình lăng trụ đứng được định nghĩa là hình có hai đa giác đáy nằm trên hai mặt phẳng song song và có hình đa giác bằng nhau. Các mặt bên của hình lăng trụ đứng là hình chữ nhật, vuông góc với mặt phẳng đáy là đa giác. Chiều cao của hình lăng trụ đứng chính là độ dài của cạnh bên. Dựa vào đa giác đáy của hình lăng trụ đứng, chúng ta có thể đặt tên cho các dạng như hình lăng trụ đứng tứ giác, hình lăng trụ đứng tam giác,...
Các tính chất của hình lăng trụ đứng bao gồm:
- Hình lăng trụ đứng có các cạnh bên vuông góc với đáy.
- Hình lăng trụ đứng có các mặt bên là hình chữ nhật.
- Mặt phẳng chứa đáy của hình lăng trụ đứng song song với nhau.
- Chiều dài cạnh bên của hình lăng trụ đứng chính là chiều cao.
Hình lăng trụ đều
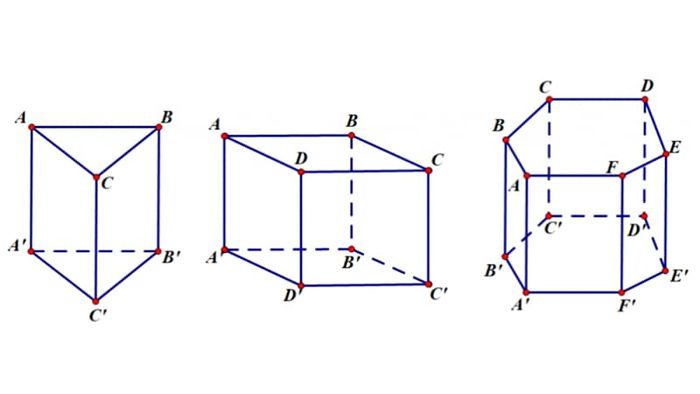
Hình lăng trụ đều được định nghĩa là hình lăng trụ vuông có đáy là đa giác đều. Trong khi học về thể tích khối lăng trụ, chắc hẳn bạn đã nghe về các loại khối lăng trụ tam giác đều, tứ giác đều,… Vì đáy của hình lăng trụ là một đa giác đều, nên các cạnh đáy sẽ bằng nhau. Ngoài ra, các cạnh bên của hình lăng trụ đều là hình chữ nhật và vuông góc với mặt đáy.
Các công thức liên quan đến hình lăng trụ
Tương tự như một số hình học không gian khác, hình lăng trụ bao gồm các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích khối lăng trụ. Các công thức này sẽ được chia sẻ ngay trong phần dưới đây để bạn có thể theo dõi!
Tính diện tích xung quanh
Cách tính diện tích xung quanh của hình lăng trụ đứng là tổng diện tích các mặt bên hoặc có thể tính bằng chu vi đáy nhân với chiều cao. Sxq = p.h (P là chu vi đáy và h là chiều cao)
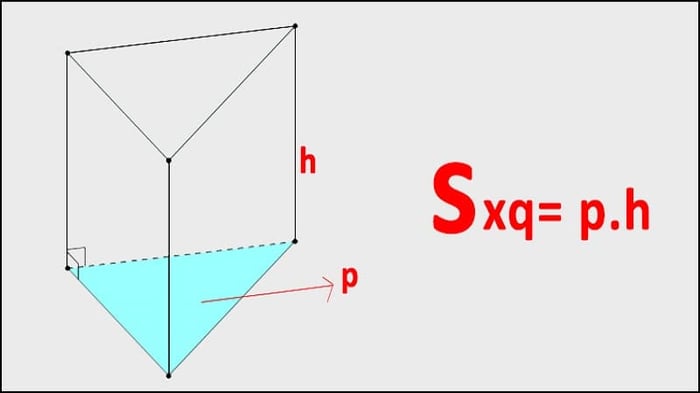
Nhìn chung, cách tính diện tích xung quanh hình lăng trụ khá đơn giản. Tuy nhiên, để giúp các bạn hiểu rõ hơn công thức này, chúng tôi sẽ cung cấp ví dụ cụ thể. Cho hình lăng trụ đứng tam giác ADCDEF. Hãy tính diện tích xung quanh của hình lăng trụ này?
Hướng dẫn giải: Theo yêu cầu của đề bài, chúng ta đã biết các cạnh của mặt đáy để tính chu vi và chiều cao. Lưu ý, đề bài yêu cầu tính diện tích xung quanh, không phải tính thể tích khối lăng trụ, do đó cần áp dụng công thức đúng. Sxq = (3+4+5) x 7 = 84 (cm2) Như vậy, chúng ta đã tính được diện tích xung quanh của hình lăng trụ ABCDEF là 84cm.
Diện tích toàn phần hình lăng trụ
Diện tích toàn phần của hình lăng trụ được tính bằng tổng diện tích xung quanh và diện tích hai đáy. Vì vậy, để tính diện tích toàn phần, ta cần tính diện tích xung quanh trước. Stp = Sxq + S2Đáy
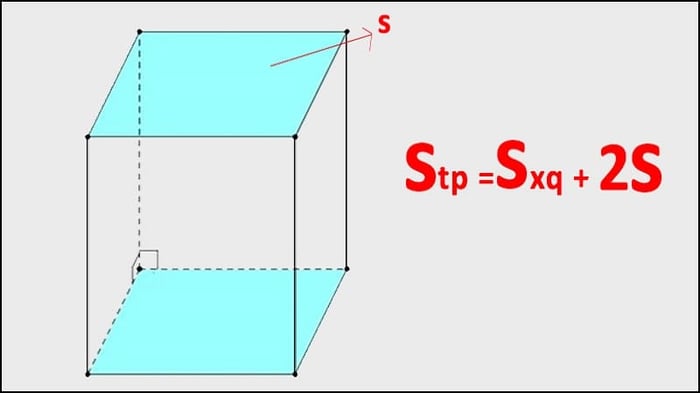
Chúng tôi sẽ tiếp tục ví dụ với hình lăng trụ ABCDEF, để tính diện tích toàn phần cần tính diện tích của hai đáy. Vì đây là hình lăng trụ tam giác, diện tích mặt đáy là 1/2 x 3 x 4 = 6 (cm2). Sau khi tính diện tích xung quanh, ta có thể tính diện tích toàn phần.
Stp = 84 + 2 x 6 = 96 (cm2) => Vậy diện tích toàn phần của hình lăng trụ ABCDEF là 96 cm2.
Thể tích khối lăng trụ
Thể tích của hình lăng trụ được áp dụng rộng rãi trong thực tế. Thể tích của hình lăng trụ đứng được tính bằng diện tích đáy nhân với chiều cao. V = Sđáy x h
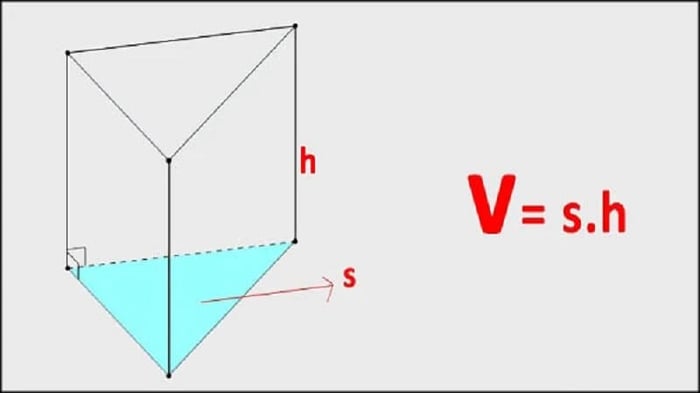
Ví dụ: Cho hình lăng trụ đứng có mặt đáy là hình chữ nhật với chiều rộng 3cm, chiều dài 4cm, chiều cao 5,5cm. Hãy tính thể tích của khối lăng trụ với các thông số đã cung cấp.
Hướng dẫn tính: Theo dữ liệu cho trước, xác định được đây là hình lăng trụ với hình dạng là hình chữ nhật. Đầu tiên, tính diện tích mặt đáy Sđáy = 3 x 4 = 12 (cm2). Sau đó, tính thể tích của hình lăng trụ bằng V = 12 x 5,5 = 66 (cm3). Vậy thể tích của hình lăng trụ là 66 cm3.
Một số dạng hình lăng trụ đặc biệt
Ngoài các loại hình lăng trụ đã đề cập, trong hình học không gian còn tồn tại một số dạng hình lăng trụ đặc biệt như hình hộp đứng, hình hộp chữ nhật, hình lập phương. Để mở rộng kiến thức về hình lăng trụ, chúng tôi sẽ giới thiệu định nghĩa và tính chất của những loại này để các bạn tham khảo:
Hình hộp đứng
Hình hộp đứng có các cạnh bên vuông góc với mặt đáy được gọi là hình hộp đứng. Đặc điểm của hình hộp đứng là mặt đáy là hình bình hành và các mặt xung quanh là hình chữ nhật.
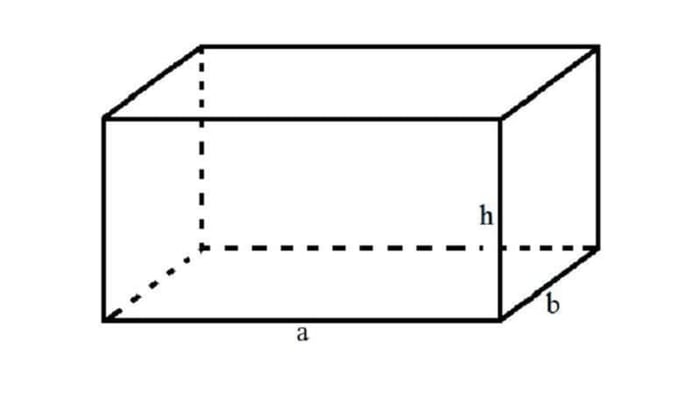
Hình hộp chữ nhật
Hình hộp có mặt đáy là hình chữ nhật được gọi là hình hộp chữ nhật. Điều này có nghĩa là hình hộp chữ nhật sẽ có tất cả 6 mặt xung quanh là hình chữ nhật. Bên cạnh đó, loại hình lăng trụ đặc biệt này có tổng cộng 12 cạnh, 8 đỉnh và 6 mặt. Hai đỉnh đối diện của hình hộp chữ nhật được nối bởi một đường chéo có hai đầu mút và cắt nhau tại một điểm. Diện tích và chu vi của các mặt đối diện của hình hộp chữ nhật bằng nhau.
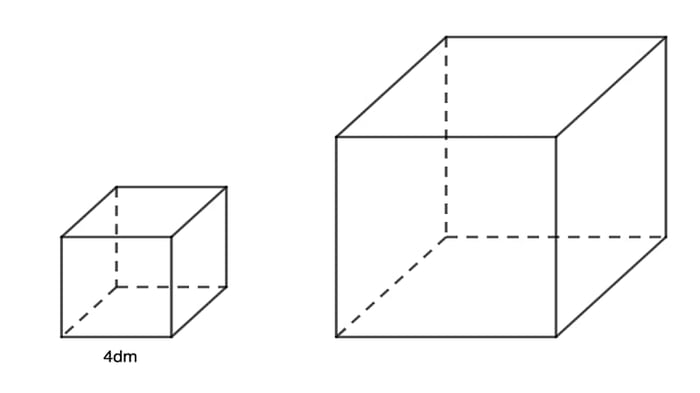
Hình lập phương
Hình lập phương thuộc nhóm các hình lăng trụ đặc biệt, có hai đáy là hình hộp chữ nhật và bốn mặt bên đều là hình vuông. Đây là một hình học đa diện với các mặt là hình vuông và mỗi đỉnh của nó là điểm giao của ba mặt.
Một số dạng bài tập về khối lăng trụ
Chúng tôi đã tổng hợp kiến thức lý thuyết, cách tính diện tích xung quanh, diện tích toàn phần, thể tích khối lăng trụ cho các bạn nắm được. Để giải những bài tập liên quan đến hình lăng trụ, các bạn cần rèn luyện chăm chỉ. Dưới đây là một số bài tập thường gặp cùng cách giải:
Bài 1
Cho hình lăng trụ với kích thước như hình dưới đây, chúng ta yêu cầu tính diện tích xung quanh và thể tích của hình lăng trụ này.
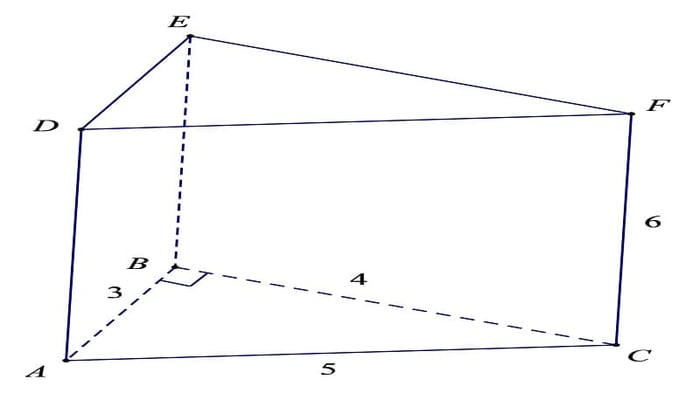
Cách làm:
Đầu tiên, chúng ta tính chu vi của mặt đáy hình lăng trụ. Theo bài toán, chu vi tam giác ABC là 12cm, chiều cao là 6cm. Sau đó tính diện tích xung quanh của hình lăng trụ ABCDEF = 12 x 6 = 72cm2.
Diện tích đáy hình lăng trụ là 6cm2 => thể tích của hình lăng trụ ABCDEF = S x h = 6 x 6 = 36cm3. Vậy đã tính được diện tích xung quanh của hình lăng trụ là 72cm2 và thể tích là 36cm3.
Bài 2
Cho hình lăng trụ đứng có đáy là hình chữ nhật, hãy tính diện tích xung quang và thể tích của hình đó?
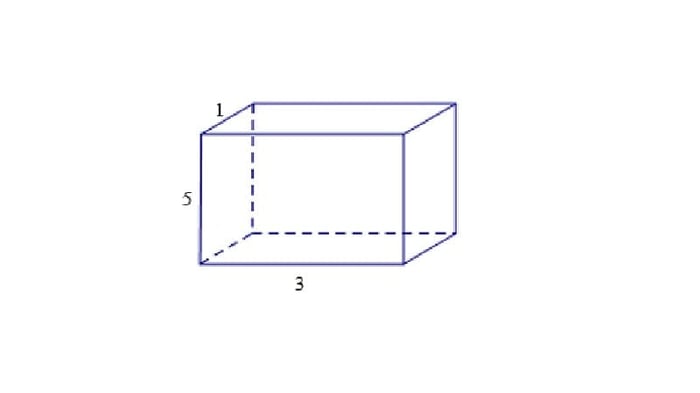
Cách làm:
Tương tự như vậy, trước tiên chúng ta tính chu vi đáy = 2.( 1+ 3) = 8 và có chiều cao là 5cm.
Diện tích hình lăng trụ chữ nhật = C x h = 8 x 5 = 40cm2.
Để tính thể tích của khối lăng trụ, ta cần tính diện tích đáy = 3 x 1 = 3cm2
Thể tích của hình lăng trụ đứng = S x h = 3 x 5 = 15cm3.
Bài 3
Dựa vào hình lăng trụ dưới đây để xác định số cạnh.
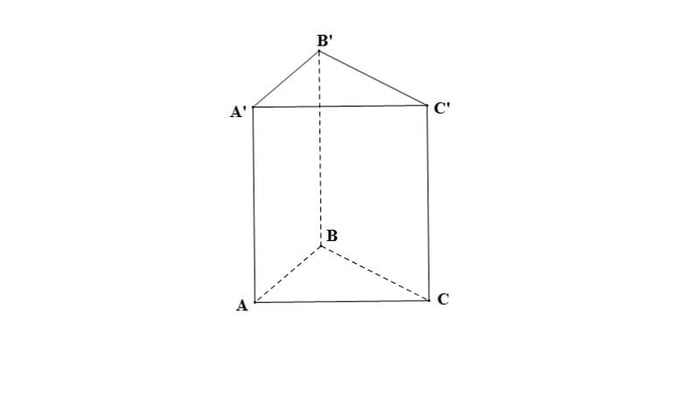
- 9 cạnh
- 8 cạnh
- 5 cạnh
- 6 cạnh
Đáp án: Theo lý thuyết, đây là hình lăng trụ đứng tam giác có 6 đỉnh, 5 mặt và 9 cạnh => đáp án đúng là A. 9 cạnh. Đây là câu hỏi lý thuyết thường gặp trong bài kiểm tra nên các bạn cần nắm chắc kiến thức nhé!
Bài 4
Cho hình lăng trụ đứng tứ giác dưới đây với kích thước chi tiết. Hãy tính thể tích của hình lăng trụ và chọn đáp án đúng?
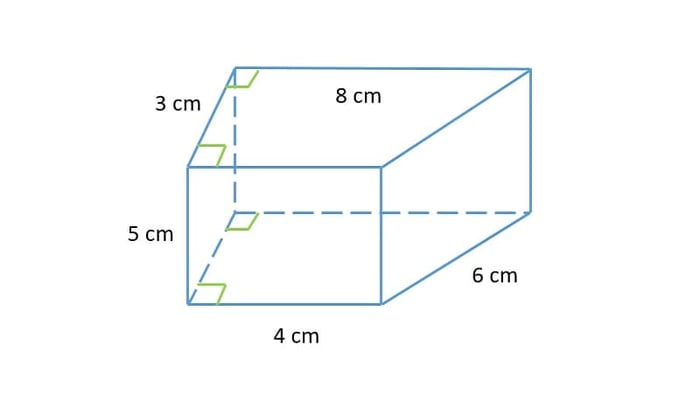
- V = 80 cm3
- V = 18 cm3
- V = 19 cm3
- V = 90 cm3
Cách làm:
Dạng bài trắc nghiệm về thể tích khối lăng trụ thường xuất hiện trong các bài kiểm tra. Theo hình lăng trụ trên, ta biết mặt đáy là hình thang bằng nhau => diện tích mặt đáy = 12.(4+8).3=18 => S=12.(4+8).3=18 (cm2)
Sau khi tính được diện tích một mặt đáy, ta tính thể tích hình lăng trụ V = 18 . 5 = 90 (cm3). Vậy đáp án đúng cho câu hỏi này là D.
Bài 5
Tiếp tục là một dạng bài cho hình lăng trụ, yêu cầu tính diện tích xung quanh rồi khoanh vào đáp án chính xác.
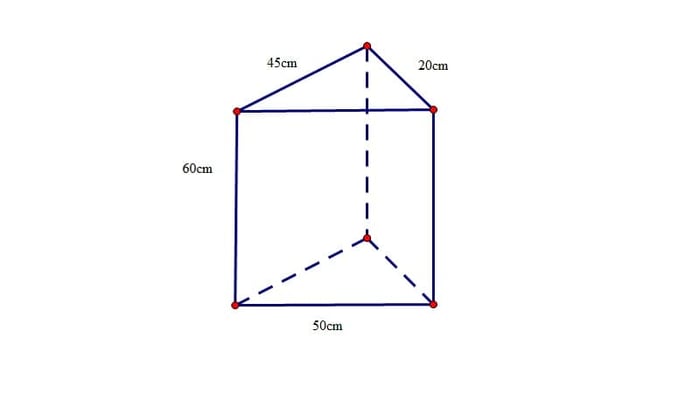
- 7 200 cm2
- 6 900 cm2
- 6 250 cm2
- 7 900 cm2
Cách làm:
Xác định đây là hình lăng trụ đứng tam giác nên có diện tích xung quanh = 45 + 20 + 50) . 60 = 6 900 (cm2). Như vậy, B là đáp án chính xác của bài tập này.
Tạm Kết
Bài viết trên, chúng tôi đã chia sẻ cách tính thể tích khối lăng trụ cho các bạn tham khảo. Bên cạnh đó, chúng tôi còn hướng dẫn giải một số dạng bài tập thường gặp. Mong rằng các bạn sẽ nắm chắc kiến thức lý thuyết đồng thời có đủ kỹ năng để giải bài tập liên quan. Hãy bấm theo dõi fanpage Mytour và kênh Mytour để không bỏ lỡ những thông tin thú vị từ chúng tôi nhé!
