1. Căn bậc ba là gì? Kiến thức về căn bậc ba
Căn bậc ba của một số thực hoặc biểu thức là x (x là số thực) hoặc X (X là biểu thức) sao cho thỏa mãn điều kiện a3 = x và A3 = X
Ký hiệu:
![sqrt[3]{x} a](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246uXJ/anh-mo-ta.png)
![sqrt[3]{x} = A](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246HNq/anh-mo-ta.png)
Chỉ số căn trong căn bậc ba là số 3
Hành động lấy căn bậc ba của một số hoặc biểu thức được gọi là khai căn bậc ba
Ví dụ:
![\sqrt[3]{27} = 3](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246lhE/anh-mo-ta.png)
Lưu ý: Mỗi số thực a chỉ có một giá trị duy nhất của căn bậc ba.
Cụ thể là:
![\sqrt[3]{a}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246wKw/anh-mo-ta.png)
![\sqrt[3]{a}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246uLh/anh-mo-ta.png)
![\sqrt[3]{a}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246YEO/anh-mo-ta.png)
2. Điều kiện áp dụng của căn bậc ba
Khác với căn bậc hai, căn bậc ba không yêu cầu số trong căn phải không âm; nó có thể là số âm hoặc số dương. Tuy nhiên, tùy vào bài toán cụ thể mà điều kiện và tập xác định có thể thay đổi (ví dụ, đối với căn bậc ba của một phân số, mẫu số phải khác 0).
3. Một số đặc điểm của căn bậc ba
.png)
Như vậy, chúng ta thấy rằng việc khai căn và các tính chất của căn bậc ba khá đơn giản và không phức tạp như căn bậc hai vì không cần phải xét dấu của giá trị.
4. Ứng dụng các tính chất của căn bậc ba
Dựa trên các tính chất đã nêu, chúng ta có thể áp dụng các quy tắc để đưa thừa số vào trong căn, khai căn, khử mẫu của biểu thức có căn bậc ba hoặc quy tắc đưa căn bậc ba ra khỏi mẫu như sau:
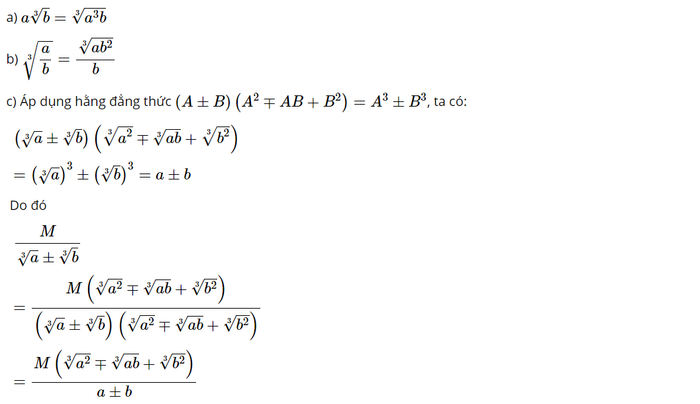
2. Các dạng toán cơ bản về căn bậc ba thường gặp
Dạng 1: Tính giá trị của căn bậc ba đối với số thực hoặc biểu thức
Để giải bài toán này, bạn cần hiểu rõ quy tắc chuyển số và giá trị vào và ra khỏi căn.
Dạng 2: So sánh các căn bậc ba
Áp dụng:
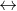
![sqrt[3]{a} nhỏ hơn sqrt[3]{b}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246hou/anh-mo-ta.png)
![sqrt[3]{26}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246Cte/anh-mo-ta.png)
Chúng ta có:
![sqrt[3]{27}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246YhU/anh-mo-ta.png)
![sqrt[3]{26} nhỏ hơn sqrt[3]{27}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246aJI/anh-mo-ta.png)
![\sqrt[3]{26} < 3](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246jWf/anh-mo-ta.png)
Loại 3: Giải các phương trình chứa căn bậc ba
![\sqrt[3]{A}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246aqO/anh-mo-ta.png)
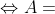
Ví dụ:
![\sqrt[3]{x - 1 }](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246STS/anh-mo-ta.png)
x - 1 = 2^3
x - 1 = 8
x = 9
3. Các bài tập áp dụng để tự rèn luyện
Câu 1: Tính giá trị của các biểu thức sau:
![(\sqrt[3]{3} + \sqrt[3]{2})](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246SjV/anh-mo-ta.png)
![(\sqrt[3]{5} - \sqrt[3]{3}) (\sqrt[3]{25} + \sqrt[3]{15})](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246RMF/anh-mo-ta.png)
![(\sqrt[3]{162} \cdot \sqrt[3]{-2}) (\sqrt[3]{2/3})](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246LRC/anh-mo-ta.png)
![\sqrt[3]{38 - 17\sqrt{5}} + \sqrt[3]{38 + 17\sqrt{5}}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246mhN/anh-mo-ta.png)
Câu 3: Cho x và y khác nhau. Chứng minh rằng biểu thức sau không phụ thuộc vào x và y
![\frac{2\sqrt[3]{2xy}}{x^2y^2} - \sqrt[3]{4} , \frac{2xy}{xy} + \sqrt[3]{2} - \frac{xy}{xy} - \sqrt[3]{2}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246NaZ/anh-mo-ta.png)
Câu 4: Kết quả so sánh nào dưới đây là sai:
![\sqrt[3]{123}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246ICu/anh-mo-ta.png)
![5\sqrt[3]{6} = 6\sqrt[3]{5}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246maz/anh-mo-ta.png)
![3\sqrt[3]{6} = 6\sqrt[3]{5}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246fcl/anh-mo-ta.png)
Câu 5: Xác định giá trị của x để các căn thức sau đều có nghĩa
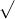
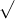
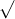
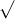
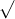
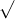
Câu 6: Xác định giá trị của x để các căn thức sau đều hợp lệ
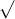
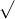
Câu 7: Xác định các giá trị của x để các căn thức sau đều có nghĩa:
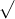
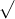
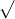
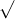
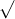
Câu 8: Xác định giá trị của x để các căn thức sau đều có nghĩa
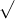
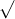
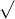
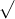
Câu 9: Thực hiện các phép toán sau:
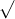
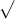
Câu 10: Xem xét biểu thức sau đây:
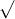
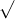
a. Xác định giá trị của x để A có ý nghĩa?
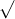
Câu 11: Xét ba số dương x, y, z với điều kiện: xy + z + zx = 1. Tính toán:
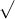
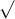
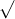
Câu 12: Giải các phương trình sau đây:
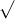
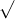
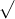
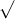
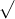
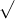
Câu 13: Tìm nghiệm của các phương trình sau đây:
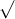
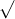
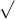
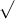
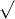
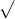
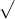
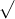
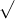
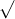
Câu 14: Tìm nghiệm cho các phương trình dưới đây:
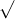
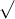
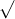
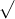
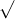
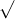
Câu 15: Giải các phương trình sau đây một cách chính xác:
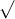
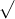
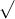
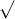
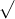
Câu 16: Xác định giá trị của x sao cho mỗi căn thức dưới đây có nghĩa
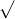
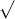
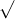
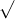
Câu 17: Đơn giản hóa các biểu thức sau đây:
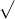
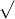
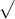
Câu 18: Đơn giản hóa các biểu thức dưới đây:
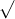
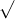
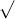
Câu 19: Xem xét biểu thức dưới đây
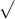
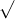
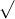
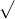
a. Xác định giá trị của x sao cho biểu thức dưới đây có nghĩa?
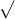
Câu 20: So sánh các biểu thức căn thức dưới đây
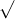
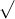
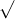
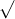
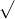
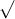
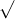
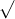
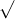
Câu 21: Thực hiện các phép toán dưới đây:
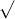
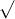
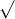
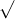
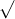
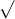
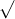
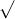
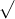
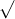
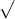
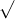
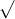
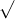
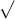
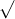
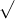
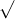
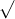
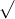
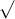
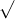
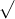
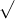
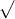
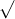
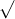
Câu 22: Phân tích đa thức ra các thừa số
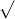
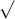
b. 4a + 1 với a < 0
Câu 23: Tìm nghiệm phương trình:
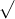
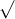
Câu 24: Xem xét biểu thức sau đây:
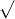
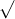
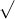
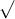
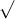
Khi x > 0 và x ≠ 1
a. Đơn giản hóa biểu thức A
b. Tìm giá trị của x sao cho A = 5/3
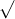
a. Tính độ dài của đoạn thẳng AB, AC, AH
b. Trên đoạn thẳng AC, chọn điểm K sao cho K không trùng với A và C. Gọi D là hình chiếu của A trên BK. Chứng minh rằng BD = BK - BH = BC
Câu 26: Thực hiện phép tính
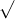
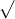
Câu 27: Xác định điều kiện của x để các biểu thức sau được xác định:
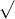
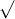
Câu 28: Đối với biểu thức P = x³ + y³ - 3(x + y) + 1993, hãy tính giá trị của P khi
![sqrt[3]{9 + 4sqrt[5]{6}}](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479246grA/anh-mo-ta.png)
Câu 29: Tiến hành phép tính sau:
Bài viết trên Mytour đã cung cấp cho bạn đọc cái nhìn sâu sắc về căn bậc ba, lý thuyết liên quan và các bài tập thực hành. Chúng tôi đã trình bày chi tiết về cách giải quyết các vấn đề và bài toán ứng dụng liên quan đến chủ đề này. Cảm ơn bạn đã theo dõi bài viết.
