Căn bậc hai là gì? Định nghĩa và ví dụ về căn bậc hai số học, chẳng hạn như căn bậc hai của số 9?

Buzz

Nội dung bài viết

1. Căn bậc hai là gì?

1.1. Định nghĩa căn bậc hai

1.2. So sánh hai giá trị căn bậc hai

1.3. Các tính chất của căn bậc hai

2. Căn bậc hai số học là gì?

2.1. Định nghĩa về căn bậc hai số học

2.2. So sánh hai giá trị căn bậc hai số học

2.3. Căn bậc hai của số nguyên dương

2.4. Căn bậc hai của số âm và số phức

3. Bài tập ứng dụng

4. Câu hỏi trắc nghiệm

Xem thêm

Căn bậc hai là gì? Cách tính căn bậc hai số học và giá trị của căn bậc hai số 9? Đọc bài viết chi tiết dưới đây để hiểu rõ hơn.

1. Căn bậc hai là gì?

1.1. Định nghĩa căn bậc hai

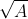
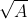
$\sqrt{A}$ $\sqrt{A}$

- Lưu ý:

Khi a >= 0, ta có

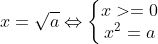
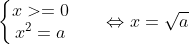
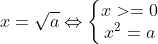
$x = \sqrt{a} \Leftrightarrow \left\{\begin{matrix} x\geq 0& & \\ x^{2}= a& & \end{matrix}\right.$ $\left\{\begin{matrix} x\geq 0 & & \\ x^{2}=a& & \end{matrix}\right.\Leftrightarrow x=\sqrt{a}$ $x=\sqrt{a}\Leftrightarrow \left\{\begin{matrix} x\geq 0 & & \\ x^{2} =a & & \end{matrix}\right.$

1.2. So sánh hai giá trị căn bậc hai

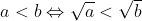
$a<b\Leftrightarrow \sqrt{a}<\sqrt{b}$

- Các hằng thức quan trọng cần nhớ:

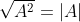
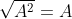
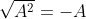
$\sqrt{A^{2}}=\left | A \right |$ $\sqrt{A^{2}}=A$ $\sqrt{A^{2}}=-A$

- Một số phép biến đổi tương đương với căn bậc hai cần biết để giải các bài toán liên quan đến căn bậc hai bao gồm:

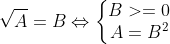
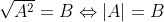
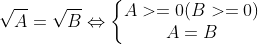
$\sqrt{A} = B \Leftrightarrow \left\{\begin{matrix} B\geq 0 & & \\ A=B^{2} & & \end{matrix}\right.$ $\sqrt{A^{2}}= B\Leftrightarrow \left | A \right |=B$ $\sqrt{A^{2}}= \sqrt{B^{2}}\Leftrightarrow \left | A \right |=\left | B \right |\Leftrightarrow A=B ext{ hoặc } A=-B$ $\sqrt{A}=\sqrt{B}\Leftrightarrow \left\{\begin{matrix} A\geq 0 ( B\geq 0) & & \\ A=B & & \end{matrix}\right.$

1.3. Các tính chất của căn bậc hai

- Mỗi số thực không âm a có đúng một căn bậc hai không âm.

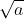
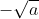
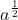
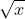
$\sqrt{a}$ $-\sqrt{a}$ $a^{\frac{1}{2}}$ $\sqrt{x}$

2. Căn bậc hai số học là gì?

2.1. Định nghĩa về căn bậc hai số học

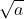
$\sqrt{a}$

Số 0 cũng chính là căn bậc hai của 0.

- Lưu ý: Khi a >= 0, ta có:

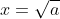
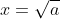
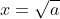
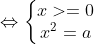
$x=\sqrt{a}$ $^{2}$ $^{2}$ $x=\sqrt{a}$ $x=\sqrt{a}$ $\Leftrightarrow \left\{\begin{matrix} x\geq 0 & & \\ x^{2}=a & & \end{matrix}\right.$

2.2. So sánh hai giá trị căn bậc hai số học

Đối với hai số không âm a và b, ta có:

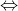
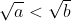
$\Leftrightarrow$ $\sqrt{a}<\sqrt{b}$

2.3. Căn bậc hai của số nguyên dương

- Một số dương có hai giá trị căn bậc hai, một dương và một âm. Tuy nhiên, khi nhắc đến căn bậc hai của số nguyên dương, thường là căn bậc hai dương.

- Căn bậc hai của một số nguyên là một số nguyên đại số.

- Căn bậc hai của một số nguyên dương được tính bằng tích các căn của các thừa số nguyên tố của nó, bởi vì căn bậc hai của một tích bằng tích của các căn bậc hai.

- Căn bậc hai của các số từ 0 đến 10

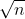
n $\sqrt{n}$ 0 01 12 1,4143 1,7324 25 2,2366 2,4497 2,6468 2,828

9 310 3,162

2.4. Căn bậc hai của số âm và số phức

- Căn bậc hai của số âm thuộc vào tập số phức, không phải số thực.

- Bình phương của bất kỳ số nào đều là số dương, trừ số 0. Vì vậy, không có số âm nào có căn bậc hai là số thực.

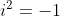
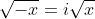
$i^{2}=-1$ $\sqrt{-x}=i\sqrt{x}$ $^{2}$

3. Bài tập ứng dụng

Bài 1: Xác định giá trị x để các căn thức bậc hai sau có nghĩa

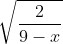
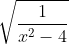
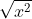
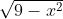
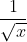
$\sqrt{\frac{2}{9-x}}$ $\sqrt{\frac{1}{x^{2}-4}}$ $\sqrt{x^{2}+2x+1}$ $\sqrt{9-x^{2}}$ $\frac{1}{\sqrt{x}+2}+\frac{\sqrt{x}}{\sqrt{x}-3}$

Bài 2: Đơn giản hóa các biểu thức sau:

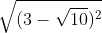
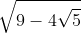
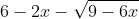
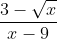
$\sqrt{(3-\sqrt{10})^{2}}$ $\sqrt{9-4\sqrt{5}}$ $6-2x-\sqrt{9-6x+x^{2}}$ $\frac{3-\sqrt{x}}{x-9}$ $\frac{x-5\sqrt{x}+6}{\sqrt{x}-3}$

Bài 3: Giải các phương trình dưới đây:

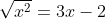
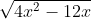
$\sqrt{x^{2}-10x+25}=2$ $\sqrt{x^{2}}=3x-2$ $\sqrt{4x^{2}-12x+9} =x+7$

Bài 4: Chứng minh rằng:

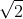
$\sqrt{2}+\sqrt{6}+\sqrt{12}+\sqrt{20}+\sqrt{30}+\sqrt{42}<24$

Bài 5: Tìm giá trị lớn nhất của biểu thức sau:

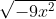
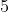
$\sqrt{3-2x^{2}}$ $\sqrt{-9x^{2}+6x+3}$ $5+\sqrt{-4x^{2}-4x}$

Bài 6: Đơn giản hóa biểu thức A

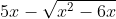
$\sqrt{\frac{(x^{2}-3)^{2}+12x^{2}}{x^{2}}}+ \sqrt{(x+2)^{2}-8x}$ Bài 7: Xét biểu thức $5x-\sqrt{x^{2}-6x+9}$

a, Đơn giản hóa biểu thức M

b, Xác định các giá trị của x sao cho M = 4

4. Câu hỏi trắc nghiệm

Câu 1: Với a > 0, lựa chọn nào dưới đây là căn bậc hai số học của a?

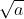
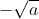
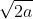
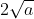
$\sqrt{a}$ $-\sqrt{a}$ $\sqrt{2a}$ $2\sqrt{a}$

Câu 2: Với số thực a > 0, căn bậc hai số học của a là x nếu và chỉ nếu:

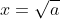
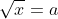
$x = \sqrt{a}$ $\sqrt{x} = a$ $a^{2} = x$ $x^{2} = a$

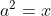
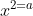
Câu 3: Căn bậc hai số học của số a = 0.36 là số nào trong các lựa chọn sau?

A. -0.6

B. 0.6

C. 0.9

D. -0.18

Câu 4: Căn bậc hai số học của số a = 2.25 là số nào trong các lựa chọn sau?

A. -1.5 và 1.5

B. 1.25

C. 1.5

D. -1.5

Câu 5: Đâu là khẳng định không đúng?

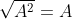
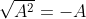
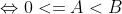
$\sqrt{A^{2}} = A$ $\sqrt{A^{2}} = -A$ $\sqrt{A} = \sqrt{B}$ $\Leftrightarrow 0 \leq A < B$

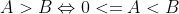Câu 6: So sánh hai số 5 và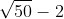 $\sqrt{50} - 2$

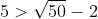
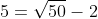
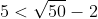
$5 = \sqrt{50} - 2$ $5 < \sqrt{50} - 2$

D. Không đủ thông tin để so sánh

Câu 9: Xét biểu thức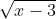 $\sqrt{x-3}$ có nghĩa khi nào

A. x < 3

B. x < 0

C. x \geq 3

D. x \geq 3

Câu 10: Xét biểu thức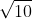 $\sqrt{10+100x}$ có nghĩa khi nào

A. x \geq -\frac{1}{10}

B. x \geq \frac{1}{10}

C. x \geq -\frac{1}{10}

D. x \geq 10

Câu 11: Tìm các giá trị x không âm sao cho căn x \geq 3

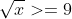
$\sqrt{x} \geq 9$

B. x < 9

C. x > 9

D. x \leq 9

Câu 12: Căn bậc hai của số 9 là

A. 3

B. -3

C. 81

D. cả A và B

Câu 13: Câu nào dưới đây là chính xác nhất?

Căn bậc hai của số 16 là

A. 4

B. -4

C. 4 hoặc -4

D. 4 và -4

Câu 14: Trong một biểu thức căn thức:

A. Dưới một dấu căn có thể chứa số hoặc chữ, nhưng không thể chứa cả hai cùng một lúc

B. Dưới một dấu căn chỉ có thể chứa các căn thức khác

C. Dưới một dấu căn chỉ có thể chứa một phân số

D. Tất cả các câu trên đều không chính xác

E. Dưới một dấu căn có thể chứa số, chữ, hoặc cả các căn thức khác cùng với các phép toán số học

Câu 15: Xét số a<0. Câu nào sau đây là sai?

A. Căn bậc hai của a là căn bậc hai số học của số không âm a

B. Số a có căn bậc hai lớn hơn 0 và nhỏ hơn 0

C. Một trong hai câu A hoặc B là câu sai

D. Ít nhất một trong hai câu A hoặc B là câu đúng

Câu 16: Khẳng định nào sau đây là chính xác?

A. Căn bậc hai của 121 là 11

B. Căn bậc hai của 144 là 12

C. Căn bậc hai của 169 là 13 và -13

D. Căn bậc hai của 144 là -12

Câu 17: Giải phương trình căn bậc hai của x = -2

A. Phương trình có nghiệm x = -4

B. Phương trình có nghiệm x = 4

C. Phương trình có nghiệm x = 4 và x = -4

D. Phương trình vô nghiệm

Câu 18: Chọn câu đúng:

A. Số dương chỉ có một căn bậc hai duy nhất

B. Số dương có hai căn bậc hai, là hai số đối nhau

C. Số dương không có căn bậc hai

D. Số dương có hai căn bậc hai, cả hai cùng dấu

Câu 19: Chọn đáp án đúng

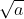
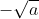
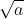
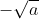
$\sqrt{a}$ $-\sqrt{a}$ $\sqrt{a}$ $-\sqrt{a}$

D. số dương không có căn bậc hai

Câu 20: Một học sinh đã thực hiện như sau:

1. chọn kết luận chính xác

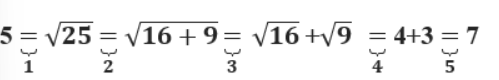
Căn bậc hai là gì? Căn bậc hai số học là gì? Căn bậc hai số học của 9 là bao nhiêu?

A. học sinh đã làm đúng

B. bạn đã sai từ bước đầu tiên

C. bạn đã sai từ bước thứ hai

D. bạn đã sai từ bước thứ ba

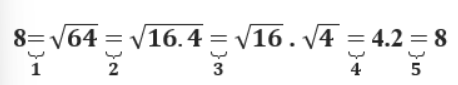
Căn bậc hai là gì? Khái niệm căn bậc hai số học? Căn bậc hai số học của 9 là bao nhiêu?

A. bạn đã thực hiện đúng

B. bạn đã mắc lỗi từ bước đầu tiên

C. bạn đã sai từ bước thứ hai

D. bạn đã sai từ bước thứ ba

Bài viết của Mytour đề cập đến Căn bậc hai là gì? Khái niệm căn bậc hai số học? Căn bậc hai số học của 9 là bao nhiêu? cùng với các đặc điểm và sự so sánh giữa các căn bậc hai số học. Hy vọng bài viết mang lại giá trị cho bạn đọc. Cảm ơn sự quan tâm của bạn!

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]