1. Khái niệm về cấp số cộng
Trong toán học, cấp số cộng là dãy số (có thể hữu hạn hoặc vô hạn) mà từ số hạng thứ hai trở đi, mỗi số hạng là tổng của số hạng trước đó cộng với một số không đổi khác 0, gọi là công sai.
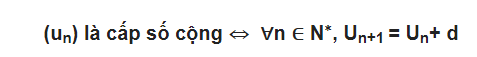
Số d được gọi là công sai trong cấp số cộng
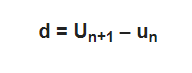
2. Đặc điểm của cấp số cộng
Trong một cấp số cộng, mỗi số hạng (ngoại trừ số hạng đầu và cuối) là trung bình cộng của hai số hạng kề nhau.
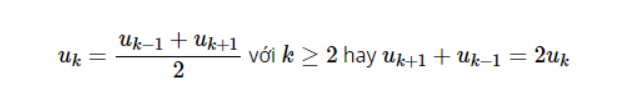
3. Công thức để tính số hạng tổng quát trong cấp số cộng
Đối với một cấp số cộng với số hạng đầu là u1 và công sai là d, số hạng tổng quát u(n) có thể được tính theo công thức sau
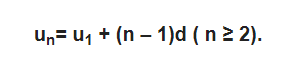
4. Công thức để tính tổng của cấp số cộng
Khi u(n) là cấp số cộng và Sn là tổng của n số hạng đầu tiên (Sn = u1 + u2 + ... + u(n)), ta có công thức tính tổng như sau
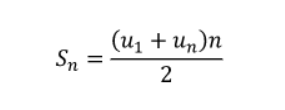
Sử dụng công thức u(n) = u1 + (n - 1) d, chúng ta có thể tính toán như sau
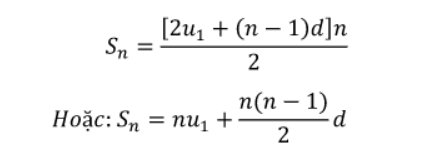
5. Ví dụ thực tiễn về cấp số cộng
Ví dụ 1: Xét cấp số cộng u(n) với u1 = -1 và d = 3. Tính S(20)
Chúng ta có
S(20) = 20 u1 + 20 × (20 - 1) / 2 × 3
= 20 × (-1) + 20 × 19 / 2 × 3
= 550
Ví dụ 2: Xét cấp số cộng u(n) với u1 = 5 và d = 4. Tính u(26)
Chúng ta có:
u(26) = u1 + (26 - 1) × d
= 5 + (26 - 1) × 4
= 105
Ví dụ 3: Xét cấp số cộng u(n) với u1 = -2 và d = 7. Tìm công thức cho số hạng tổng quát
u(n) = u1 + (n - 1) × d
= -2 + (n - 1) × 7
= 7n - 9
Ví dụ 4: Xét cấp số cộng u(n) với u1 = 1 và tổng của 100 số hạng đầu là 24850. Tính công sai d
Chúng ta có S(100) = 24850
⇔ n / 2 × (u1 + u(n)) = 24850
⇔ u(100) = 496
Ta có u(100) = u1 + 99 × d
⇔ d = (u(100) - u1) / 99
⇔ d = 5
6. Bài tập thực hành
Câu 1: Dãy số 3, 6, 9, 12, 15 là cấp số cộng vì lý do gì?
Câu 2: Với cấp số cộng u(n) có u1 = -2 và công sai d = 7, hãy tính số hạng tổng quát?
Câu 3: Xét cấp số cộng u(n) với d = 3 và u1 = -1. Tính tổng S(100)
Câu 4: Cho cấp số cộng u(n) với tổng của 100 số hạng đầu là 2400 và u1 = 1. Tính công sai d của cấp số cộng là bao nhiêu?
Câu 5: Xác định bốn số hạng liên tiếp của một cấp số cộng sao cho tổng của chúng là 20 và tổng của bình phương của chúng là 120.
Câu 6: Với cấp số cộng có u1 = -3 và u6 = 27, hãy tính công sai d?
A. d = 5
B. d = 7
C. d = 6
D. d = 8
Câu 7: Với cấp số cộng có u1 = 1/3 và u8 = 26, tính công sai d?
A. d = 11/3
B. d = 3/11
C. d = 10/3
D. d = 3/10
Câu 8: Với cấp số cộng u(n) có u1 = -0,1 và d = 0,1, số hạng thứ 7 của cấp số cộng này là:
A. 1,6
B. 6
C. 0,5
D. 0,6
Câu 9: Với cấp số cộng u(n) có u1 = -0,1 và d = 1, khẳng định nào sau đây là chính xác?
A. Số hạng thứ 7 của cấp số cộng này là 0,6
B. Cấp số cộng này không chứa các số 0,5 và 0,6
C. Số hạng thứ 6 của cấp số cộng này là 0,5
D. Số hạng thứ 4 của cấp số cộng này là 3,9
Câu 10: Xác định bốn số hạng liên tiếp của một cấp số cộng sao cho tổng của chúng là 20 và tổng các bình phương của chúng là 120
A. 1, 5, 6, 8
B. 2, 4, 6, 8
C. 1, 4, 6, 9
D. 1, 4, 7, 8
Câu 11: Xét dãy số u(n) = 1 / (2n + 1)
A. Dãy số này không phải là cấp số cộng
B. Số hạng thứ n + 1: u(n + 1) = 1 / (2n)
C. Hiệu giữa hai số hạng liên tiếp: u(n + 1) - u(n) = 1 / (2n(2n + 1))
D. Tổng của năm số hạng đầu tiên là S(5) = 12
Câu 12: Xét dãy số u(n) với u(n) = 2n + 5. Khẳng định nào dưới đây là sai?
A. Là cấp số cộng với công sai d = -2
B. Là cấp số cộng với công sai d = 2
C. Số hạng thứ n + 1: u(n + 1) = 2(n + 1) + 5 = 2n + 7
D. Tổng của bốn số hạng đầu tiên là S(4) = 40
Câu 13: Với dãy số u(n) có công sai d = -2 và tổng 8 số hạng đầu tiên là 72, tính giá trị của u1?
A. u1 = 16
B. u1 = -16
C. u1 = 1/16
D. u1 = -1/16
Câu 14: Với dãy số u(n) có công sai d = 0,1 và tổng 5 số hạng đầu tiên là -0,5, hãy tính giá trị của u1?
A. u1 = 0,3
B. u1 = 10/3
C. u1 = -10/3
D. u1 = -0,3
Câu 15: Với dãy số u(n) có số hạng đầu u1 = -1, công sai d = 2 và tổng của n số hạng là 483, hãy tính số lượng số hạng của cấp số cộng này?
A. n = 20
B. n = 21
C. n = 22
D. n = 23
Câu 16: Dãy số u(n) có phải là cấp số cộng không? Nếu có, hãy xác định công sai của nó. Biết rằng:
1. u(n) = 2n + 3
A. d = -2
B. d = 3
C. d = 5
D. d = 2
2. u(n) = -3n + 1
A. d = -2
B. d = 3
C. d = -3
D. d = 1
3. u(n) = n^2 + 1
A. d = Ø
B. d = 3
C. d = -3
D. d = 1
4. u(n) = 2 / n
A. d = Ø
B. d = 1 / 2
C. d = -3
D. d = 1
Câu 17: Xác định xem các dãy số dưới đây có phải là cấp số cộng không? Nếu có, hãy tìm công sai của chúng
1. u(n) = 3n + 1
A. d = Ø
B. d = 3
C. d = -3
D. d = 1
2. u(n) = 4 - 5n
A. d = Ø
B. d = -5
C. d = -5
D. d = 1
3. u(n) = (2n + 3) / 5
A. d = Ø
B. d = 2 / 5
C. d = -3
D. d = 1
4. u(n) = (n + 1) / n
A. d = Ø
B. d = 3
C. d = -3
D. d = 1
5. u(n) = n / 2^n
A. d = Ø
B. d = 3
C. d = -3
D. d = 1
6. u(n) = n^2 + 1
A. d = Ø
B. d = 3
C. d = -3
D. d = 1
Câu 18: Xét cấp số cộng u(n) với u1 = -0,3 và u8 = 8. Đâu là khẳng định sai?
A. Số hạng thứ hai của cấp số cộng này là 1,4
B. Số hạng thứ ba của cấp số cộng này là 2,5
C. Số hạng thứ tư của dãy số cộng này là 3,6
D. Số hạng thứ bảy của dãy số cộng này là 7,7
Câu 19: Xem xét dãy số u(n) với u(n) = 7 - 2n. Khẳng định nào dưới đây là không đúng?
A. Ba số hạng đầu tiên là u1 = 5, u2 = 3, u3 = 1
B. Số hạng thứ n+1 là u(n+1) = 8 - 2n
C. Cấp số cộng này có công sai d = -2
D. Số hạng thứ tư là u4 = -1
Câu 20: Xét dãy số u(n) với u1 = √2, d = √2, và tổng S = 21√2. Khẳng định nào dưới đây là chính xác?
A. S là tổng của năm số hạng đầu của dãy số cộng
B. S là tổng của sáu số hạng đầu của dãy số cộng
C. S là tổng của bảy số hạng đầu tiên trong cấp số cộng
D. S là tổng của bốn số hạng đầu tiên trong cấp số cộng
Đây là bài viết của Mytour về khái niệm cấp số cộng, công sai và công thức liên quan cùng các bài tập thực hành. Hy vọng bài viết sẽ hữu ích cho bạn. Xin chân thành cảm ơn!
