Cây Cân Bằng AVL

Trong lĩnh vực khoa học máy tính, một Cây Cân Bằng AVL là loại cây tìm kiếm nhị phân có khả năng tự cân bằng, và là cấu trúc dữ liệu đầu tiên đạt được điều này. Ở mỗi nút của cây AVL, sự chênh lệch chiều cao giữa hai cây con không vượt quá một. Do đó, các phép chèn (insertion) và xóa (deletion) đều có thời gian thực hiện O(log n) trong cả trường hợp trung bình lẫn trường hợp tồi tệ nhất. Việc bổ sung và loại bỏ có thể yêu cầu tái cân bằng qua một hoặc nhiều phép quay.

Tên gọi của cây AVL được đặt theo hai nhà sáng lập, G.M. Adelson-Velsky và E.M. Landis, được công bố trong bài báo của họ vào năm 1962: 'An algorithm for the organization of information.' (Một thuật toán về tổ chức thông tin)

Cây AVL thường được so sánh với cây đỏ đen vì cả hai đều hỗ trợ các phép toán cơ bản với thời gian thực hiện O(log n). Cây AVL thường hoạt động hiệu quả hơn cây đỏ đen trong các ứng dụng cần hiệu suất cao. Các thuật toán cân bằng của cây AVL thường được trình bày trong các giáo trình về khoa học máy tính.

Khái niệm

Hệ số cân bằng

Hệ số cân bằng của cây T là sự chênh lệch chiều cao giữa cây con bên trái và bên phải của nó. Ký hiệu hệ số cân bằng của cây con gốc u là balance(u). Hệ số cân bằng của cây T được ký hiệu là balance(T).

balance(u)= height(u.right)-height(u.left)

Nếu mọi đỉnh u của cây T đều có balance(u)= 0, thì T được gọi là cây cân bằng hoàn toàn. Nếu balance(T) > 0, tức là cây con bên phải cao hơn cây con bên trái, thì T được gọi là cây lệch phải. Ngược lại, nếu balance(T) < 0, tức là cây con bên trái cao hơn cây con bên phải, thì T được gọi là cây lệch trái.

Cân bằng AVL và cây AVL

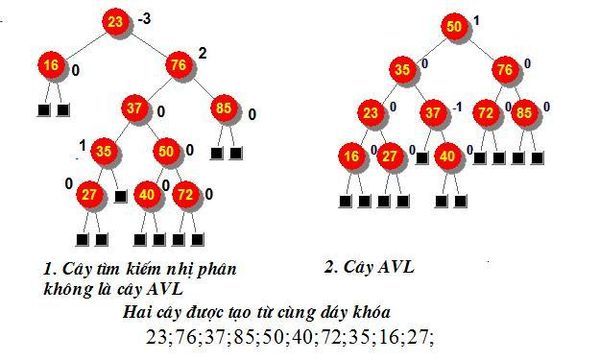
Các cây tìm kiếm nhị phân được tạo dựng theo cách chèn thông thường có thể gặp phải sự mất cân đối nghiêm trọng, ví dụ như hoàn toàn lệch phải (tất cả các nút chỉ có con phải) hoặc lệch trái (tất cả các nút chỉ có con trái). Trong những trường hợp này, chi phí tìm kiếm trong tình huống xấu nhất có thể lên tới n (n là số nút trong cây). Nếu cây tìm kiếm nhị phân được cân bằng hoàn toàn, chi phí chỉ khoảng log₂n. Tuy nhiên, không phải lúc nào cũng có thể tạo ra một cây tìm kiếm nhị phân cân bằng hoàn toàn cho mọi dãy khóa. G.M. Adelson-Velsky và E.M. Landis đã đề xuất một tiêu chuẩn cân bằng, sau này được gọi là cân bằng AVL, giúp giảm bớt yêu cầu so với cân bằng hoàn toàn. Cây T được gọi là cây cân bằng AVL nếu tại mỗi nút u của nó, hệ số cân bằng không vượt quá 1 về trị tuyệt đối. Điều này có nghĩa là với mọi nút u của T, balance(u) chỉ nhận một trong ba giá trị: -1, 0, hoặc 1. Khi đó, cây T được gọi là cây AVL. Nếu cây con gốc tại nút u là cân bằng AVL, thì nút u cũng được xem là cân bằng AVL. Ví dụ, các lá là cây AVL, cây chỉ có một nút là cây AVL, cây chỉ có hai nút là cây AVL, cây có ba nút có thể là cây AVL hoặc không.

Phép chèn

Quá trình chèn và tính cân bằng AVL

Giả sử chúng ta có một cây tìm kiếm nhị phân cân bằng AVL và u là một nút trong cây

T, và một nút mới v được chèn vào vị trí của u. Vì v chỉ có thể được chèn vào một trong hai cây con của u, nên tối đa v chỉ có thể làm tăng chiều cao của một trong hai cây con này. Nếu v không làm tăng chiều cao của cây con nào, hoặc làm tăng chiều cao của một cây con nhưng trước đó cây con này có chiều cao nhỏ hơn hoặc bằng chiều cao của cây con còn lại, thì tính cân bằng AVL tại nút u vẫn không thay đổi. Tính cân bằng AVL tại u chỉ có thể bị ảnh hưởng nếu v làm tăng chiều cao của cây con có chiều cao lớn hơn trong hai cây con của u.

Tương tự, nếu v không làm tăng chiều cao của chính u, thì v không làm thay đổi hệ số cân bằng tại các nút tổ tiên của u.

Ngoài ra, nút v luôn được chèn vào với tư cách là con của một nút đã là lá hoặc nửa lá trước đó.

Nếu nút cha của v trước khi chèn v là nửa lá, thì chiều cao của cây con gốc của cha của v không thay đổi sau khi thêm v, và hệ số cân bằng tại nút cha này sẽ là 0. Trong trường hợp này, tất cả các nút tổ tiên của cha của v cũng không thay đổi hệ số cân bằng. Tính cân bằng AVL được duy trì trên toàn cây T.

Nếu nút cha của v trước khi chèn v là lá, thì gọi u là nút tổ tiên của v có mức cao nhất mà tại đó tính cân bằng AVL bị phá vỡ.

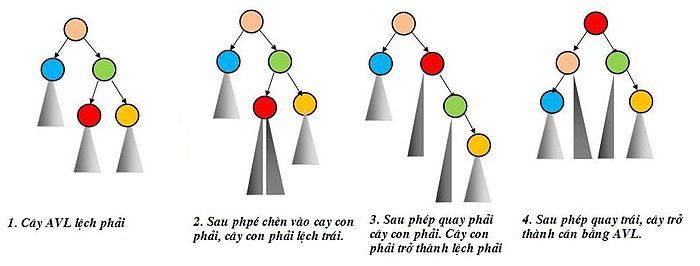
Có bốn trường hợp có thể làm mất tính cân bằng AVL tại u

1. Trước khi chèn, nếu cây con gốc tại u bị lệch trái và v làm tăng chiều cao của cây con trái.
   1. .Sau khi chèn, nếu cây con trái bị lệch trái (Trường hợp LL);
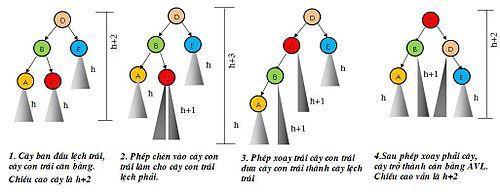
   2. .Sau khi chèn, nếu cây con trái bị lệch phải (Trường hợp LR).
2. .Trước khi chèn, nếu cây con gốc tại u bị lệch phải và v làm tăng chiều cao của cây con phải.
   1. .Sau khi chèn, nếu cây con phải bị lệch phải (Trường hợp RR);
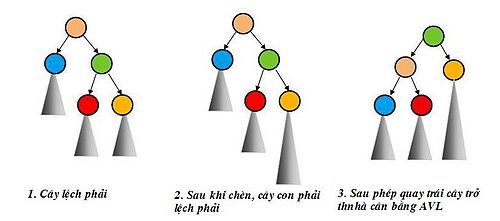
   2. .Sau khi chèn, nếu cây con phải bị lệch trái (Trường hợp RL).

Quá trình tái cân bằng sau khi chèn

Khi tính cân bằng AVL tại u bị phá vỡ, cần thực hiện một hoặc hai phép quay để tái cân bằng cây con gốc tại u và điều chỉnh cây T để đạt được trạng thái cân bằng AVL.

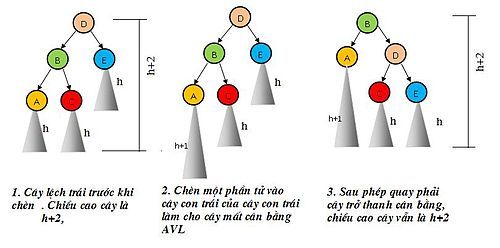
Thực hiện phép quay sang phải tại nút u.

Trước tiên, thực hiện phép quay sang trái tại u.left để chuyển về trạng thái TH1 (LL), sau đó thực hiện phép quay sang phải tại u.

Thực hiện phép quay sang trái tại nút u.

Trước hết thực hiện phép quay phải tại u.right để đưa về TH3 (RR) sau đó thực hiện phép quay trái tại u.

Nhận diện mã giả

Trong đoạn mã giả này, height(u) biểu thị chiều cao của cây con tại nút u. Nếu nút u là lá, thì height(u)=1. Đối với bất kỳ nút u nào không phải là lá, height(u)=max{height(u.left),height(u.right)}+1. Có thể sử dụng duyệt hậu để tính giá trị height(u) cho tất cả các nút trên cây T. Tuy nhiên, khi thêm một nút mới vào cây (luôn là lá), ta cần cập nhật giá trị height(v) cho mọi nút v là tổ tiên của nút đó.

CALCULATE-BALANCE(u)
 // Tính toán hệ số cân bằng và chiều cao của cây con tại nút u.
 if  u.right = Null and u.left=Null then
     begin
         height(u)=1;
         balance(u)=0
     end; 
 else
     if u.right = Null and u.left<>Null then 
         begin
             height(u)=height(u.left)+1;
             balance(u)=height(u)
         end
     else  
         if u.left = Null and u.right<>Null then 
             begin
                 height(u)=height(u.right)+1;
                 balance(u)=-height(u)
             end;
         else
             begin
                 height(u)=max(height(u.left),height(u.right))+1;
                 balance(u)=height(u.left)-height(u.right);
             end;

REBALANCE(v)
  // Thủ tục này tái cân bằng AVL cho các nút tổ tiên của v nếu bị mất cân bằng.
  // Sau đó, các tổ tiên trên sẽ không thay đổi hệ số cân bằng từ trước khi v được thêm vào.
  // v là lá 
  // Tìm nút tổ tiên v có chỉ số tuyệt đối của v  
  u= v
  while u<> T.root and abs(balance(u)) ≤1 do 
      begin 
          CALCULATE-BALANCE(u)
          u=u.parent;
      end;   
  if balance(u)>2 then 
      if balance(u.left)>0 then
          RIGHT-ROTATE(u)
      else
          begin
              LEFT-ROTATE(u.left);
              RIGHT-ROTATE(u);
          end;
  else
      if balance(u)<-2 then
          if balance(u.right)< 0 then
              LEFT-ROTATE(u)
          else
              begin
                  RIGHT-ROTATE(u.right);
                  LEFT-ROTATE(u);
              end;

Phương pháp xóa trên cây AVL

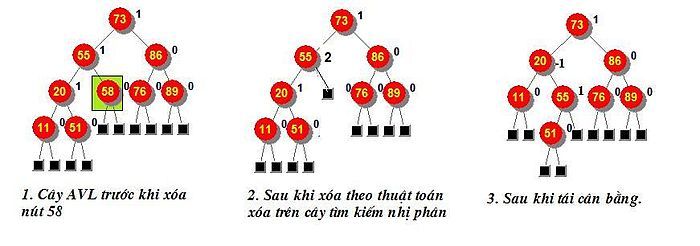
Khi xóa nút v trên cây AVL, trước tiên thực hiện xóa giống như trên cây tìm kiếm nhị phân thông thường. Nút v sẽ được thay thế bằng một nút lá hoặc nút nửa lá với con trái. Giả sử p là cha của v, v1 là con trái của v (có thể là NULL). Khi xóa v, ta thay v bằng con trái v1. Chiều cao và hệ số cân bằng của cây con gốc v1 không thay đổi, nhưng chiều cao và hệ số cân bằng của nút cha p có thể thay đổi. Trong trường hợp này, áp dụng thủ tục REBALANCE(p) như khi chèn nút.

• Cây đỏ đen
• Cây 2-3-4