Cây tìm kiếm nhị phân (viết tắt là BST - Binary Search Tree) là một cấu trúc dữ liệu phổ biến được sử dụng để giải quyết các vấn đề tìm kiếm. Mỗi cây nhị phân có tính chất: Đối với mỗi nút , các nút trong cây con bên trái đều có giá trị key nhỏ hơn , và các nút trong cây con bên phải đều có giá trị key lớn hơn hoặc bằng .
Định nghĩa
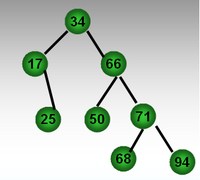
Cây nhị phân dành cho n khóa là cây nhị phân trong đó mỗi nút có một khóa, sao cho với mỗi nút k:
- Mọi khoá trên cây con trái đều nhỏ hơn khoá trên nút k
- Mọi khoá trên cây con phải đều lớn hơn khoá trên nút k
Cây tìm kiếm nhị phân là một cấu trúc dữ liệu cơ bản được sử dụng để xây dựng các cấu trúc dữ liệu trừu tượng hơn như các tập hợp, đa tập hợp, các dãy kết hợp.
Nếu một BST chứa các giá trị giống nhau thì nó biểu diễn một tập hợp đa phần. Cây loại này sử dụng các bất đẳng thức không nghiêm ngặt. Mọi nút trong cây con trái có khoá nhỏ hơn khoá của nút cha, mọi nút trên cây con phải có nút lớn hơn hoặc bằng khoá của nút cha.
Nếu một BST không chứa các giá trị giống nhau thì nó biểu diễn một tập hợp đơn trị như trong lý thuyết tập hợp. Cây loại này sử dụng các bất đẳng thức nghiêm ngặt. Mọi nút trong cây con trái có khoá nhỏ hơn khoá của nút cha, mọi nút trên cây con phải có khoá lớn hơn khoá của nút cha.
Việc lựa chọn đặt các giá trị bằng nhau vào cây con phải (hoặc trái) là tùy thuộc vào người dùng. Một số người cũng đặt các giá trị bằng nhau vào cả hai phía, nhưng khi đó việc tìm kiếm trở nên phức tạp hơn.
Các phép toán trên cây tìm kiếm nhị phân
Tìm kiếm (Searching)
Việc tìm kiếm một khoá trên cây tìm kiếm nhị phân có thể thực hiện thông qua đệ quy. Quá trình bắt đầu từ gốc. Nếu khoá cần tìm bằng khoá của gốc thì khoá đó được tìm thấy trên cây. Nếu khoá cần tìm nhỏ hơn khoá của gốc, ta tiếp tục tìm kiếm trên cây con trái, và nếu khoá cần tìm lớn hơn khoá của gốc, ta tiếp tục tìm kiếm trên cây con phải. Nếu cây con trái hoặc phải là rỗng, thì khoá cần tìm không có trên cây.
Giải mã
Tìm_kiếm_nhị_phân(node, key);
nếu node là Null thì
trả về None; /* không tìm thấy khóa /
nếu khóa < node.key:
trả về tìm_kiếm_nhị_phân(node.trái, khóa);
ngược lại
nếu khóa > node.key
trả về tìm_kiếm_nhị_phân(node.phải, khóa)
ngược lại / khóa bằng với khóa của nút */
trả về node.giá_trị; # tìm thấy khóa
Mã Python:
def tìm_kiếm_nhị_phân(node, khóa):
nếu node là None:
trả về None # khóa không được tìm thấy
nếu khóa < node.khóa:
trả về tìm_kiếm_nhị_phân(node.con_trái, khóa)
elif khóa > node.khóa:
trả về tìm_kiếm_nhị_phân(node.con_phải, khóa)
ngược lại: # khóa bằng với khóa của nút
trả về node.giá_trị # tìm thấy khóa
Thời gian tìm kiếm trung bình là O(log 2n), và là O(n) khi cây là không cân bằng chỉ là một danh sách liên kết.
Chèn (Insertion)
Phép chèn vào cây nhị phân giống như phép tìm kiếm; Nếu khóa của nút gốc khác khóa cần chèn, ta tìm nó trong cây con trái hoặc cây con phải. Nếu cây con trái hoặc cây con phải là trống (không tìm thấy), thêm một nút mới và gán khóa cần chèn cho nút đó.
Dưới đây là đoạn mã trong ngôn ngữ C++:
void ChènNút(cấu trúc node *&treeNode, cấu trúc node *nútMới)
{ //Chèn con trỏ nút 'nútMới' vào cây con bắt đầu bởi 'treeNode'
if (treeNode == NULL)
treeNode = nútMới; //Chỉ thay đổi 'node' khi nó là NULL
else if (nútMới->giá trị < treeNode->giá trị)
ChènNút(treeNode->trái, nútMới);
else
ChènNút(treeNode->phải, nútMới);
}
Mã ngôn ngữ Python:
def chèn_cây_nhị_phân(nút, khóa, giá_trị):
if nút là None:
return NútCây(None, khóa, giá_trị, None)
if khóa == nút.khóa:
return NútCây(nút.trái, khóa, giá_trị, nút.phải)
if khóa < nút.khóa:
return NútCây(chèn_cây_nhị_phân(nút.trái, khóa, giá_trị), nút.khóa, nút.giá_trị, nút.phải)
else:
return NútCây(nút.trái, nút.khóa, nút.giá_trị, chèn_cây_nhị_phân(nút.phải, khóa, giá_trị))
Phương pháp Xóa (Deletion)
Xem xét các tình huống sau đây
- Xóa một lá: Vì lá không có con, ta chỉ cần giải phóng nó khỏi cây.
- Xóa nút có một con: Xóa và thay thế nút đó bằng con duy nhất của nó.
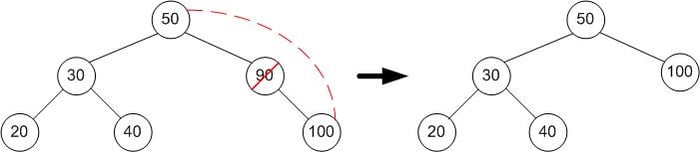
- Xóa một nút có hai con: Xóa nút đó và thay thế nó bằng nút có khóa lớn nhất trong các khóa nhỏ hơn khóa của nó (gọi là 'nút tiền nhiệm' - nút cực phải của cây con trái) hoặc nút có khóa nhỏ nhất trong các khóa lớn hơn nó (gọi là 'nút kế vị' - nút cực trái của cây con phải)
Có thể thay đổi vị trí nút tiền nhiệm hoặc nút kế vị với nút cần xóa và sau đó xóa nó. Bởi vì những nút này có không quá hai con, việc xóa chúng có thể giải quyết bằng hai trường hợp đã nêu.
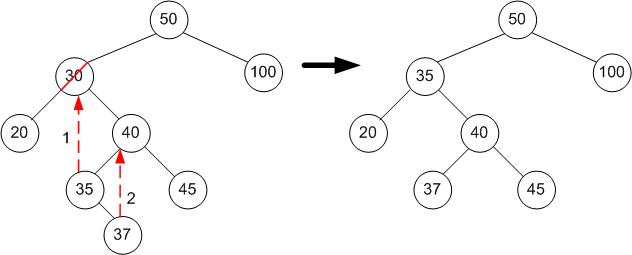
Dưới đây là đoạn mã C++
void XóaNút(struct node*& node) {
if (node->left == NULL) {
struct node* temp = node;
node = node->right;
delete temp;
} else if (node->right == NULL) {
struct node* temp = node;
node = node->left;
delete temp;
} else {
// Tiền nhiệm theo thứ tự (con phải nhất của cây con trái)
// Nút có hai con - lấy giá trị lớn nhất của cây con trái
struct node** temp = &(node->left); // lấy nút con trái của nút gốc
// tìm nút con phải nhất của cây con của nút con trái
while ((*temp)->right != NULL) {
temp = &((*temp)->right);
}
// sao chép giá trị từ nút con phải nhất của cây con trái sang nút gốc
node->value = (*temp)->value;
// sau đó xóa nút con phải nhất của cây con trái vì giá trị của nó
// đã được sao chép vào nút gốc
XóaNút(*temp);
}
}Đây là đoạn mã Python:
def tìmMin(self):
'''
Tìm phần tử nhỏ nhất là con của self
'''
node_hiện_tại = self
while node_hiện_tại.con_trái:
node_hiện_tại = node_hiện_tại.con_trái
return node_hiện_tại
def thayThếNútTrongCha(self, giá_trị_mới=None):
'''
Loại bỏ tham chiếu đến self từ self.parent và thay thế nó bằng giá_trị_mới.
'''
if self == self.cha.con_trái:
self.cha.con_trái = giá_trị_mới
else:
self.cha.con_phải = giá_trị_mới
if giá_trị_mới:
giá_trị_mới.cha = self.cha
def xóa_nhị_phân_cây(self, khóa):
if khóa < self.khóa:
self.con_trái.xóa_nhị_phân_cây(khóa)
elif khóa > self.khóa:
self.con_phải.xóa_nhị_phân_cây(khóa)
else: # xóa khóa ở đây
if self.con_trái và self.con_phải: # nếu cả hai con đều có mặt
# lấy nút nhỏ nhất lớn hơn self
thay_thế = self.con_phải.tìmMin()
self.khóa = thay_thế.khóa
# nếu thay_thế có một con, thay thế nó bằng đó
# ở thời điểm này, nó chỉ có thể có một con_phải
thay_thế.thayThếNútTrongCha(thay_thế.con_phải)
elif self.con_trái hoặc self.con_phải: # nếu nút chỉ có một con
nếu self.con_trái:
self.thayThếNútTrongCha(self.con_trái)
khác:
self.thayThếNútTrongCha(self.con_phải)
khác: # nút này không có con
self.thayThếNútTrongCha(None)
Thuật toán duyệt
Khi xây dựng một cây tìm kiếm nhị phân, các nút có thể được duyệt theo thứ tự giữa thông qua việc duyệt đệ quy cây con bên trái, in nút hiện tại, và sau đó duyệt đệ quy cây con bên phải. Với mọi cây nhị phân, cả hai cách duyệt theo thứ tự trước() và theo thứ tự sau() đều hữu ích.
Mã mẫu cho phép duyệt theo thứ tự giữa trong C++:
void duyệt_cây_nhị_phân(cấu trúc node* n)
{
nếu(n==null) //Cây rỗng
trả về NULL;
ngược lại
{
duyệt_cây_nhị_phân(n->left); //Duyệt cây con trái theo thứ tự giữa
printf('%d',n.key); //Thăm nút
duyệt_cây_nhị_phân(n->right); //Duyệt cây con phải theo thứ tự giữa
}
}Phép duyệt có độ phức tạp tính toán là Ω(n), bởi vì nó phải duyệt qua tất cả các nút. Độ phức tạp này cũng là O('n').
Sắp xếp
Một cây tìm kiếm nhị phân có thể được dùng như một giải thuật sắp xếp đơn giản và hiệu quả. Tương tự như heapsort, chúng ta chèn tất cả các giá trị cần sắp xếp vào một cây tìm kiếm nhị phân và in ra kết quả theo thứ tự:
def tạo_cây_nhị_phân(giá_trị):
cây = None
cho v trong giá_trị:
cây = chèn_vào_cây_nhị_phân(cây, v)
trả về cây
def lấy_duyệt_theo_thứ_tự_giữa(gốc):
'''
Trả về một danh sách chứa tất cả các giá trị trong cây, bắt đầu từ gốc.
Duyệt cây theo thứ tự giữa (câyConBênTrái, gốc, câyConBênPhải).
'''
kết_quả = []
duyệt_cây_nhị_phân(gốc, hàm phần_tử: kết_quả.append(phần_tử))
trả về kết_quả
Trường hợp xấu nhất của tạo_cây_nhị_phân có độ phức tạp là —nếu nhập vào một dãy giá trị đã sắp xếp, cây nhị phân sẽ không có nút trái. Ví dụ, lấy_duyệt_theo_thứ_tự_giữa([1, 2, 3, 4, 5]) tạo thành cây (1 (2 (3 (4 (5))))).
Có một số cách để khắc phục trường hợp này với các cây nhị phân đơn giản; cách đơn giản nhất là sử dụng cây nhị phân cân bằng tự động. Khi áp dụng thủ tục này với cây nhị phân cân bằng, trường hợp xấu nhất có độ phức tạp là O(nlog n).
Viết mã giả bằng ngôn ngữ C
Các loại cây tìm kiếm nhị phân
AVL và cây đỏ đen là các dạng cây tìm kiếm nhị phân tự cân bằng.
