1. Đề thi môn Toán lớp 10 tỉnh Quảng Ninh
Câu 1:
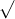
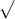
b. Tìm hệ số a sao cho đồ thị của hàm số y = ax² đi qua điểm A (1;2)
c. Giải hệ phương trình sau đây:
2x + y = 7
x - 2y = -4
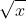
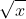
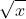
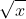
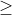
Câu 2: Xét phương trình
x^2 - 2(m + 1)x - 9 = 0 với m là biến số
a. Giải phương trình khi m = 3
b. Tìm giá trị của m để phương trình có nghiệm x = 2
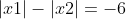
Câu 3: Hai điểm A và B cách nhau 280 km. Hai chiếc ô tô cùng khởi hành từ A đến B. Biết rằng xe đầu tiên có tốc độ nhanh hơn xe thứ hai 10 km/h và xe đầu tiên đến B trước xe thứ hai 30 phút. Tính vận tốc của từng xe.
Câu 4: Xét nửa đường tròn với tâm O và đường kính BC. Trong nửa đường tròn (O), chọn điểm A (khác B và C), gọi H là hình chiếu của A trên BC. Trên cung AC của nửa đường tròn (O), chọn điểm D (khác A và C), gọi E là hình chiếu của A trên BD, và I là giao điểm của các đường thẳng AH và BD.
a. Chứng minh rằng tứ giác ABHE là tứ giác nội tiếp.
b. Chứng minh rằng BI.BD = BH . BC.
c. Chứng minh rằng hai tam giác AHE và ACD đồng dạng.
d. Hai đường thẳng AE và DH giao nhau tại điểm F. Chứng minh rằng IF song song với AD.
Câu 5: Một thợ cơ khí cần cắt một cây sắt dài 100 dm thành các đoạn để hàn lại thành một khung hình lập phương và một hình hộp chữ nhật. Biết rằng hình hộp chữ nhật có chiều dài gấp 6 lần chiều rộng và chiều cao bằng chiều rộng (như hình minh họa). Tìm độ dài của các đoạn sắt để tổng thể tích của hai hình là nhỏ nhất.
2. Đáp án cho đề thi môn Toán tỉnh Quảng Ninh
Câu 1: Thực hiện phép tính sau
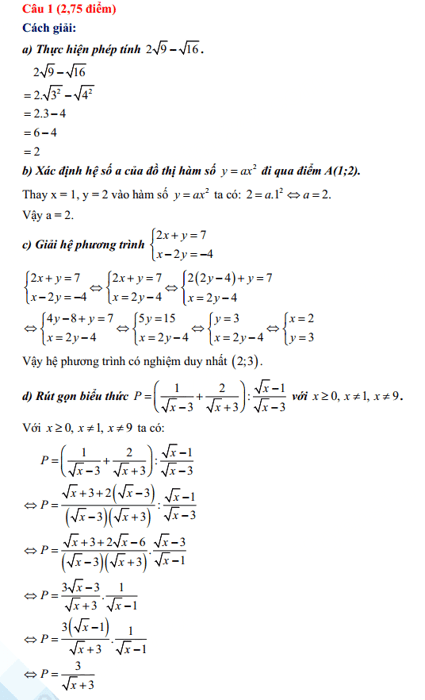
Câu 2:
a. Với m = 3, phương trình trở thành: x² - 8x - 9 = 0

Từ đó, phương trình có hai nghiệm phân biệt:
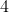
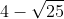
Do đó, S = (9; -1)
b. Vì phương trình có nghiệm x = 2, ta thay x = 2 vào phương trình để được:
2² - 2(m + 1) × 2 - 9 = 0
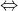
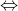
Do đó, để phương trình có nghiệm x = 2, ta có m = -9/4
c. Xem xét phương trình x² - 2(m + 1)x - 9 = 0 với a.c = -9 < 0, nên phương trình luôn có hai nghiệm trái dấu x1 và x2
Áp dụng công thức Vieta, ta có: x1 + x2 = 2(m + 1)
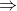
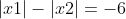
-x1 - x2 = -6
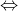
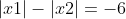
Câu 3:
Gọi vận tốc của xe thứ hai là x (km/h), với x > 0
Vận tốc của xe thứ nhất nhiều hơn xe thứ hai 10 km/h, vì vậy vận tốc của xe thứ nhất là x + 10 (km/h)
Thời gian để xe thứ nhất di chuyển từ A đến B là: 280 / (x + 10) (giờ)
Thời gian xe thứ hai đi từ A đến B là: 280 / x (giờ)
Vì xe thứ nhất đến B sớm hơn xe thứ hai 30 phút, tương đương 1/2 giờ, nên ta có:
280/x - 280/(x + 10) = 1/2
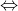
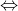
3. Các dạng bài tập ôn luyện môn Toán lớp 10
Câu 1: Xét tam giác ABC với ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF giao nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P.
1. Chứng minh rằng tứ giác CEHD là tứ giác nội tiếp
2. Các điểm B, E, F, C đều nằm trên cùng một đường tròn
3. AE.AC = AH.AD và AD.BC = BE.AC
4. H và M là hai điểm đối xứng qua đường thẳng BC
5. Tìm tâm của đường tròn nội tiếp tam giác DEF
Câu 2: Xét tam giác cân ABC (AB = AC), với các đường cao AD, BE cắt nhau tại H. O là tâm của đường tròn ngoại tiếp tam giác AHE.
1. Chứng minh tứ giác CEHD là tứ giác nội tiếp
2. Các điểm A, E, D, B nằm trên cùng một đường tròn
3. Chứng minh rằng ED = 1/2 BC
4. Chứng minh DE là tiếp tuyến của đường tròn (O)
5. Tính độ dài của DE khi DH = 2cm và AH = 6cm
Câu 3: Xét nửa đường tròn với đường kính AB = 2R. Kẻ hai tiếp tuyến từ A và B lần lượt là à và By. Qua điểm M thuộc nửa đường tròn, kẻ tiếp tuyến thứ ba cắt các tiếp tuyến à và By tại các điểm C và D. Các đường thẳng AD và BC cắt nhau tại N. Chứng minh rằng:
1. Tổng AC và BD bằng CD
2. Góc COD bằng 90 độ
3. Tích AC và BD bằng một phần tư AB
4. OC song song với BM
5. AB là tiếp tuyến của đường tròn với đường kính CD
6. MN vuông góc với AB
7. Xác định vị trí của M sao cho chu vi của tứ giác ACDB là nhỏ nhất
Câu 4: Cho đường tròn (O; R), từ điểm A trên đường tròn, vẽ tiếp tuyến d tại A. Trên đường thẳng d, chọn một điểm M khác A, vẽ cát tuyến MNP và K là trung điểm của NP. Vẽ tiếp tuyến MB tại B (B là tiếp điểm). Vẽ AC vuông góc với MB, BD vuông góc với MA, gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB
1. Chứng minh rằng tứ giác AMBO là tứ giác nội tiếp
2. Chứng minh rằng các điểm O, K, A, M, B cùng thuộc một đường tròn
3. Chứng minh rằng OAHB là hình thoi
4. Chứng minh rằng ba điểm O, H, M nằm trên một đường thẳng
5. Xác định quỹ tích của điểm H khi điểm M di chuyển dọc theo đường thẳng d
Câu 5. Xét tam giác ABC vuông tại A với đường cao AH. Vẽ đường tròn tâm A bán kính AH, gọi HD là đường kính của đường tròn này. Tiếp tuyến tại D của đường tròn cắt CA tại điểm E.
1. Chứng minh rằng tam giác BEC là tam giác cân
2. Gọi I là hình chiếu của A lên BE, chứng minh rằng AI = AH
3. Chứng minh rằng BE là tiếp tuyến của đường tròn (A; AH)
4. Chứng minh rằng BE = BH + DE
Câu 6. Xét đường tròn (O) với đường kính BC, điểm A nằm trên cung BC. Trên tia AC, lấy điểm D sao cho AB = AD. Xây dựng hình vuông ABED; AE cắt đường tròn (O) tại điểm F; tiếp tuyến tại B cắt đường thẳng DE tại điểm G.
a. Chứng minh tứ giác BGDC là tứ giác nội tiếp và xác định tâm I của tứ giác này
b. Chứng minh tam giác BFC là tam giác vuông cân và điểm F là tâm đường tròn ngoại tiếp tam giác BCD
c. Chứng minh tứ giác GEFB là tứ giác nội tiếp
Câu 7: Trong tam giác ABC với ba góc nhọn nội tiếp đường tròn (O), tiếp tuyến tại B và C của đường tròn cắt nhau tại D. Từ điểm D, vẽ đường thẳng song song với AB, cắt đường tròn tại E và F, và cắt AC tại I (E thuộc cung nhỏ BC).
a. Chứng minh rằng tứ giác BDCO là tứ giác nội tiếp
b. Chứng minh tứ giác DOIC là tứ giác nội tiếp
c. Chứng minh rằng I là trung điểm của đoạn FE
Câu 8: Trên hai cạnh góc vuông xOy, chọn hai điểm A và B sao cho OA = OB. Một đường thẳng qua A cắt OB tại M (M nằm trên đoạn OB). Từ điểm B, hạ đường vuông góc với AM tại H, và đường này cắt kéo dài của AO tại điểm I.
a. Chứng minh rằng tứ giác OMHI là tứ giác nội tiếp
b. Xác định giá trị của góc OMI
c. Vẽ đường vuông góc từ O đến BI tại điểm K. Chứng minh rằng đoạn OK bằng đoạn KH
Bài viết trên Mytour đã cung cấp thông tin chi tiết về đề thi môn toán vào lớp 10 tại tỉnh Quảng Ninh. Luật Minh Khê cũng đã đăng tải đề bài và đáp án. Cảm ơn bạn đọc đã theo dõi bài viết.
