Chiến lược làm bài hiệu quả cho Graph of a linear function trong SAT Math

Khái quát về dạng bài Graphs of linear equations and functions

• a là hệ số góc (độ dốc) của đường thẳng.

• b là tung độ của giao điểm giữa đường thẳng và trục Oy.

Đồ thị của một hàm tuyến tính luôn là một đường thẳng, điều này giúp phân biệt với dạng đồ thị đặc trưng của các loại hàm khác, ví dụ như đồ thị hàm số bậc hai là các parabol. Đồ thị tuyến tính được sử dụng để mô hình hóa các tình huống thực tế khi có tốc độ thay đổi không đổi, chẳng hạn như tốc độ, giá cả hoặc nhiệt độ thay đổi theo thời gian.

Chiến thuật cho dạng bài Graphs of linear functions

Xác định độ dốc của đường thẳng

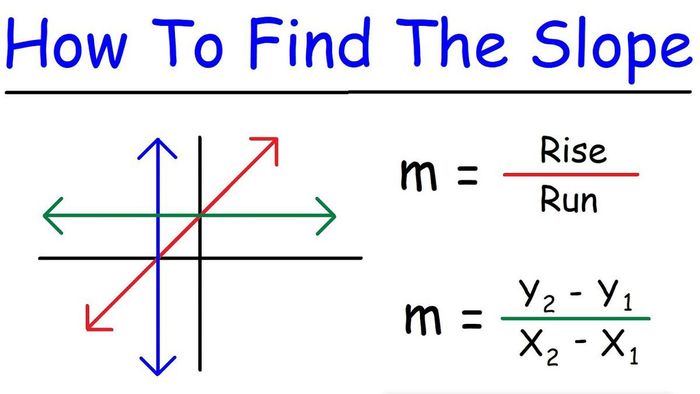
Hệ số góc hay độ dốc của đường thẳng là đại lượng đo lường sự thay đổi của đường thẳng trong quá trình di chuyển trên trục Ox. Với đồ thị của phương trình và hàm số tuyến tính, độ dốc dương cho biết đồ thị đi lên từ trái sang phải (đồng biến), trong khi độ dốc âm cho thấy đồ thị giảm dần từ trái qua phải (nghịch biến). Nếu độ dốc bằng không, đường thẳng nằm ngang, biểu thị hàm số tuyến tính đặc biệt (y = m với m là hằng số). Nếu độ dốc không xác định, đường thẳng là đường nằm dọc, biểu thị hàm đặc biệt (x = n với n là hằng số)

Trong dạng Graph of linear equations in two variables, độ dốc được tính bằng tỉ lệ thay đổi theo trục tung và tỉ lệ thay đổi theo trục hoành. Lấy hai điểm (x1, y1) và (x2, y2) bất kỳ thuộc một đường thẳng, độ dốc của đường thẳng đó là:

độ dốc = sự thay đổi theo trục tung/ sự thay đổi theo trục hoành = (y2 - y1)/ (x2 - x1)

Với phương trình dạng y = ax + b, độ dốc của đường thằng là giá trị a.

Slope = (19 - 7)/(9 - 3) = 12/6 = 2

The slope of line m is 2.

Dịch nghĩa:

Độ dốc = (19 - 7)/(9 - 3) = 12/6 = 2

Vậy độ dốc của đường thẳng m là 2.

Ví dụ 2: What is the slope of the graph 2x − 5y = 15? (Độ dốc của đường thẳng 2x - 5y = 15 là?)

2x - 5y = 15

⇔ 2x - 5y - 2x = 15 - 2x

⇔ -5y = 15 - 2x

⇔ y = (2/5)x - 3

The slope of the graph is 2/5

Tìm điểm cắt với trục Ox và Oy

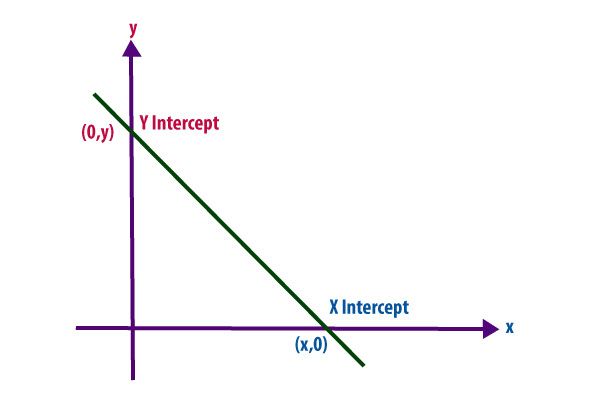
• Để tìm giao điểm của đồ thị phương trình và hàm số tuyến tính với trục Ox (x - intercept), người học thay y = 0 vào phương trình rồi giải ra tìm x. Cặp số (x, 0) với x vừa tìm được là toạ độ giao điểm của đường thẳng đã cho với trục hoành.

• Để tìm giao điểm của đồ thị phương trình và hàm số tuyến tính với trục Oy (y - intercept), người học thay x = 0 vào phương trình rồi giải ra tìm y. Cặp số (0, y) với y vừa tìm được là toạ độ giao điểm của đường thẳng đã cho với trục tung.

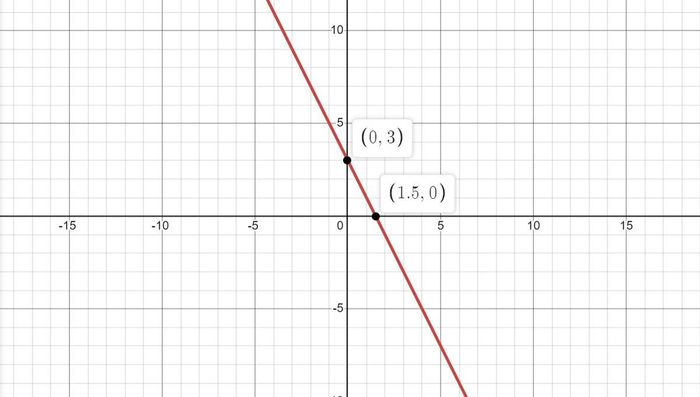
With y = 0, 3 - 2x = 0 ⇔ x = 3/2

The y - intercept of the line is located at (0, 3)

The x - intercept of the line is located at (3/2, 0)

Dịch nghĩa:

Với x = 0, y = 3 - 2 × 0 = 3.

Với y = 0, 3 - 2x = 0 ⇔ x = 3/2

Toạ độ giao điểm của y = 3 - 2x với Oy là (0, 3)

Toạ độ giao điểm của y = 3 - 2x với Ox là (3/2, 0)

Find the equation of the line

• Xác định phương trình đường thẳng khi biết hệ số góc và một điểm thuộc đường thẳng: người học thay các giá trị vào phương trình tổng quát y = ax + b, rồi tiến hành giải phương trình tìm b

• Xác định phương trình đường thẳng khi biết hai điểm thuộc đường thẳng đó: tính hệ số góc của đường thẳng, sau đó thay một trong hai điểm vào phương trình tổng quát y = ax + b, rồi tiến hành giải phương trình tìm b

Ví dụ 1: If line c has a slope of 3 and passes through the point (−2,−5), what is the equation of line c? [Nếu đường thằng c có hệ số góc là 3 và đi qua điểm (-2, -5), phương trình của đường thẳng c là?]

Plug a = 3, x = -2 and y = -5 into y = ax + b and solve for b:

-5 = 3 × (-2) + b

⇔ -5 = -6 + b

⇔ b = (-5) - (-6)

⇔ b = (-5) + 6

⇔ b = 1

The equation of line c is y = 3x + 1

Dịch nghĩa:

Thay a = 3, x = -2 và y = -5 vào y = ax + b, ta có:

-5 = 3 × (-2) + b

⇔ -5 = -6 + b

⇔ b = (-5) - (-6)

⇔ b = (-5) + 6

⇔ b = 1

Vậy phương trình đường thẳng c là y = 3x + 1.

Ví dụ 2: Line d passes through the points (3,7) and (6,−2). What is the equation of line d? [Đường thẳng d đi qua hai điểm (3, 7) và (6, -2). Phương trình của đường thẳng d là?]

The slope of line b is (-2 - 7)/(6 - 3) = -9/ 3 = -3

Use the point (3, 7) and slope a = -3 to calculate b.

Plug x = 3, y = 7 and a = - 3 into y = ax + b

7 = - 3 × 3 + b

⇔ 7 = - 9 + b

⇔ 7 + 9 = - 9 + b + 9

⇔ b = 16

The equation of line d is y = - 3x + 16

Dịch nghĩa:

Độ dốc của đường thẳng d là: (-2 - 7)/(6 - 3) = -9/ 3 = -3

Sử dụng điểm (3, 7) và độ dốc để tính b

Thay x = 3, y = 7 và a = 3 vào y = ax + b:

7 = - 3 × 3 + b

⇔ 7 = - 9 + b

⇔ 7 + 9 = - 9 + b + 9

⇔ b = 16

Phương trình đường thẳng d là y = - 3x + 16

Lines that are parallel, coincident, intersecting, or perpendicular

Xét hai đường thẳng y1 = ax + b và y2 = mx + n

• y1 cắt y2 khi: a ≠ m

• y1 song song với y2 khi: a = m và b ≠ n (parallel lines)

• y1 trùng với y2 khi: a = m và b = n

• y1 vuông góc với y2 khi: a × m = -1 (perpendicular lines)

Ứng dụng bài tập về The graph of a linear function

Bài 2: What is the slope of the graph of the equation −7x + 3y = 21?

Bài 3: If line b has a slope of −1/2​ and passes through the point (4, 7), what is the equation of line b?

Bài 4: Line e passes through the points (−1, 4) and (2, 10). What is the equation of line e?

Bài 5: Line g is represented by the equation y = 4x + 1. What is the equation of a line that is perpendicular to line g and intersects line g at the point (−2,−7)?

Solutions

Bài 1: 3

Bài 2: 7/3

Exercise 3: y = (-1/2)x + 9

Exercise 4: y = 2x + 6

Exercise 5: y = (-1/4)x - 15/2

Summary