Chứng minh tam giác cân Cách chứng minh tam giác cân

Tam giác cân là gì? Cách chứng minh tam giác cân như thế nào? Mời quý thầy cô cùng các bạn học sinh lớp 8 theo dõi bài viết dưới đây.

Chứng minh tam giác cân là tài liệu hữu ích được biên soạn đầy đủ lý thuyết, tính chất, cách chứng minh và các dạng bài tập có đáp án kèm theo. Qua đó giúp học sinh củng cố, nắm vững chắc kiến thức nền tảng, vận dụng với các bài tập cơ bản để đạt được điểm số cao trong kì thi học kì môn Toán. Vậy sau đây là nội dung chi tiết tài liệu Cách chứng minh tam giác cân, mời các bạn cùng theo dõi tại đây.

1. Cách chứng minh tam giác cân

Cách chứng minh một tam giác là tam giác cân ta sử dụng một trong hai cách sau:

• Cách 1: Chứng minh tam giác đó có hai cạnh bằng nhau.
• Cách 2: Chứng minh tam giác đó có hai góc bằng nhau.

Xem ví dụ dưới đây để nắm được cách chứng minh tam giác cân.

Ví dụ: Trong tam giác ABC có ΔABM = ΔACM . Chứng minh tam giác ABC cân.

+ Chứng minh theo cách 1:

Theo bài ra, ta có:

ΔABM = ΔACM

⇒ AB = AC

⇒ Tam giác ABC cân tại A

+ Chứng minh theo cách 2:

Theo bài ra, ta có:

∆ABM = ∆ACM

⇒ Góc B = C

⇒ Tam giác ABC cân tại A

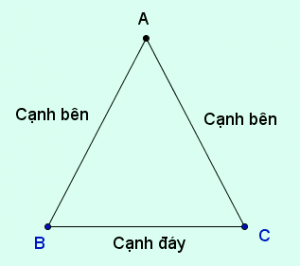
2. Tam giác cân là gì

Tam giác cân là tam giác có 2 cạnh bên bằng nhau.

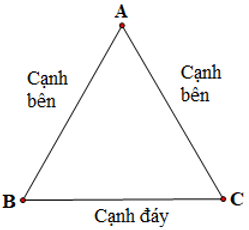
Từ hình vẽ, chúng ta có thể nhận biết được:

– Đỉnh A của tam giác cân ABC là điểm giao của hai cạnh AB và AC.

– Góc A là góc đỉnh, còn hai góc B và C được gọi là góc đáy.

3. Cách dựng tam giác ABC cân tại A

– Bắt đầu vẽ cạnh BC

– Vẽ cung tròn có tâm là B, bán kính r

– Vẽ cung tròn có tâm là C, bán kính r

• Hai cung tròn giao nhau tại điểm A.
• Cần vẽ tam giác ABC.

4. Tính chất của tam giác cân

– Tính chất 1: Trong tam giác cân, hai góc đáy bằng nhau.

Ví dụ: Trong tam giác ABC, nếu ABC cân tại A ⇒ Góc B = C

– Tính chất 2: Một tam giác có hai góc bằng nhau là tam giác cân.

Ví dụ: Trong tam giác ABC, nếu góc B = C ⇒ Tam giác ABC cân tại A

– Tính chất 3: Trường hợp đặc biệt của tam giác cân:

Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.

Ví dụ: Trong tam giác MNP, nếu MNP vuông tại M và góc N = P ⇒ Tam giác MNP là tam giác vuông cân tại M

Tính số đo mỗi góc nhọn của tam giác vuông cân.

Ta có: Trong tam giác ABC, góc A = 90°, góc B = C

⇒ Góc B + C = 90° (định lý tổng ba góc của một tam giác)

⇒ 2.Ĉ = 90°

⇒ Góc B = C = 45°

Kết luận: Trong tam giác vuông cân, hai góc nhọn đều bằng 45°.

5. Bài tập chứng minh tam giác cân

Bài 1: Trong các tam giác ở các hình 15a, b, c, d, tam giác nào là tam giác cân, tam giác nào là tam giác đều ? Vì sao ?

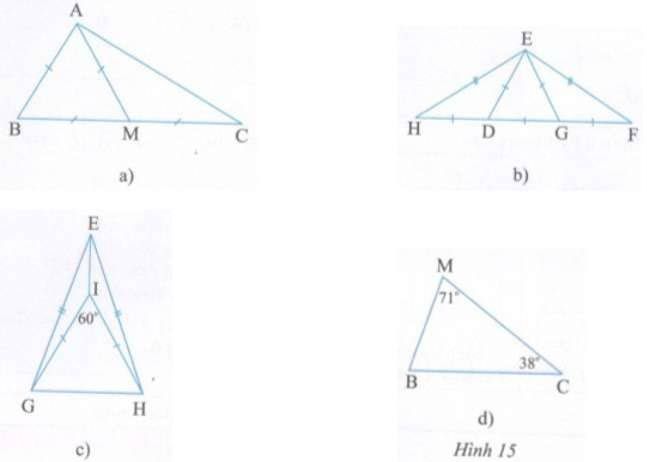
Giải:

a) Với AB = BM = AM (giả thiết) => tam giác ABM là tam giác đều.

AM = CM (giả thiết) => tam giác MAC cân tại M.

b) Dựa vào ED = DG = EG (giả thiết) => tam giác EDG là tam giác đều.

DH = DE => tam giác DEH cân tại D.

Dựa vào EG = GF => tam giác GEF cân tại G.

Ta thấy: EH = EF => tam giác EHF cân tại E.

c) Dựa vào IG = IH (giả thiết) => tam giác IGH cân tại I. Và góc GIH=60^o (giả thiết). Vì vậy tam giác IGH là tam giác đều.

Ta có: EG = EH (giả thiết) => tam giác EGH cân tại E.

d) Trong tam giác MBC, tổng các góc là 180^o

Vì vậy: 71^o + góc B = 38^o = 180^o => Góc B = 180^o – 71^o -38^o = 71^o

Ta thấy: Góc B = góc M (=71^o ) => tam giác CBM cân tại C

Bài 2: Cho hình 16, biết ED = EF; EI là tia phân giác của góc DEF.

Chứng minh rằng:

a) Tam giác EID = tam giác EIF.

b) Tam giác DIF là tam giác cân.

Giải:

a) Xét tam giác EID và EIF:

+ Dựa vào ED = EF (giả thiết)

+ Góc IED= Góc EIF (EI là tia phân giác của góc DEF)

+ EI là cạnh chung.

→ Vậy: tam giác EID ≅ tam giác EIF (theo công cụ cặp góc cân)