Chứng minh trong toán học

Trong lĩnh vực toán học, một chứng minh là một phương pháp thuyết phục (dựa trên các tiêu chuẩn đã được công nhận) để chứng minh rằng một tuyên bố toán học là chính xác. Chứng minh phải được xây dựng từ các lý luận suy diễn, không phải từ các tranh luận kiểu quy nạp hoặc kinh nghiệm. Điều này có nghĩa là, một chứng minh phải chứng minh rằng một tuyên bố là đúng trong mọi trường hợp, không có ngoại lệ. Một phát biểu chưa được chứng minh nhưng được chấp nhận là đúng gọi là một giả thuyết.

Những tuyên bố đã được chứng minh thường được gọi là định lý. Sau khi một tuyên bố đã được chứng minh, nó có thể được sử dụng làm cơ sở để chứng minh các tuyên bố khác. Một định lý cũng có thể được gọi là bổ đề, đặc biệt nếu nó được sử dụng như một bước đệm để chứng minh một định lý khác.

Lịch sử

Các tranh luận dựa trên các công cụ có sẵn như hình ảnh hay mô hình là cơ sở cho các chứng minh toán học chính xác. Sự phát triển của chứng minh toán học chủ yếu bắt nguồn từ nền văn minh Hy Lạp. Thales (624–546 TCN) đã chứng minh một số định lý trong hình học. Eudoxus (408–355 TCN) và Theaetetus (417–369 TCN) đã phát triển các định lý nhưng chưa chứng minh chúng. Aristoteles (384–322 TCN) cho rằng các định nghĩa cần được mô tả bằng những khái niệm đã biết. Euclid (300 TCN) đã bắt đầu từ những thuật ngữ chưa được định nghĩa là các tiên đề (các mệnh đề sử dụng những thuật ngữ chưa định nghĩa được giả thiết là hiển nhiên đúng, từ Hy Lạp là 'axios' nghĩa là 'một thứ có giá trị') và đã dùng chúng để chứng minh các định lý qua lý luận suy diễn. Lý thuyết chứng minh hiện đại xem các chứng minh như các cấu trúc dữ liệu được định nghĩa một cách quy nạp. Người ta không còn giả định rằng các tiên đề lúc nào cũng 'đúng đắn'; điều này cho phép xây dựng các lý thuyết toán học song song dựa trên các tập tiên đề khác nhau (như Lý thuyết tập hợp tiên đề và Hình học phi Euclid).

Các phương pháp chứng minh

Chứng minh trực tiếp

Trong chứng minh trực tiếp, kết quả được đạt được bằng cách kết hợp lôgic các tiên đề, định nghĩa và định lý đã biết. Ví dụ, có thể chứng minh rằng tổng của hai số nguyên chẵn luôn là số chẵn bằng phương pháp này:

Cho hai số nguyên chẵn bất kỳ $x$ và $y$ có thể viết dưới dạng $x=2a$ và $y=2b$ với các số nguyên $a$ và $b$. Vì cả $x$ và $y$ đều là bội số của 2. Tổng $x+y=2a+2b=2(a+b)$ cũng là bội của 2, do đó theo định nghĩa, nó là số chẵn.

Chứng minh này áp dụng định nghĩa về số nguyên chẵn và quy tắc phân phối.

Chứng minh bằng phương pháp quy nạp toán học

Trong phương pháp chứng minh bằng quy nạp toán học, trước tiên ta sẽ chứng minh 'trường hợp cơ sở'. Sau đó, sử dụng một 'luật quy nạp' để xác nhận rằng tất cả các trường hợp tiếp theo đều đúng, dù số lượng có thể là vô tận. Nếu trường hợp cơ sở đã được xác nhận đúng, thì mọi trường hợp khác cũng phải đúng, mặc dù không thể chứng minh trực tiếp tất cả chúng. Một biến thể của quy nạp là phương pháp 'xuống thang', thường dùng để chứng minh tính vô tỷ của căn bậc hai của 2.

Nguyên tắc quy nạp toán học được mô tả như sau: Cho N = { 1, 2, 3, 4,... } là tập hợp các số tự nhiên và P(n) là một phát biểu liên quan đến số tự nhiên n thuộc N sao cho

• (i) P(1) đúng, tức là P(n) đúng khi n = 1
• (ii) P(n + 1) đúng bất cứ khi nào P(n) đúng, nghĩa là nếu P(n) đúng thì P(n + 1) cũng phải đúng.

Khi đó, P(n) sẽ đúng với mọi số tự nhiên n.

Các nhà toán học thường sử dụng cụm từ 'chứng minh quy nạp' như một cách viết tắt cho phương pháp chứng minh bằng quy nạp toán học. Tuy nhiên, thuật ngữ này cũng xuất hiện trong logic để chỉ những lập luận dựa trên suy diễn quy nạp.

Chứng minh bằng phương pháp chuyển vế

Chứng minh bằng phương pháp chuyển vế giúp hình thành kết luận 'nếu p thì q' bằng cách chứng minh phát biểu tương đương 'nếu không q thì không p'.

Chứng minh bằng phương pháp phản chứng

Trong chứng minh bằng phương pháp phản chứng (hay còn gọi là reductio ad absurdum, nghĩa là 'giảm đến mâu thuẫn' trong tiếng La-tinh), ta chứng minh rằng nếu một phát biểu nào đó xảy ra, sẽ dẫn đến một mâu thuẫn về mặt logic, từ đó chứng minh phát biểu đó không thể xảy ra. Phương pháp này là một trong những phương pháp phổ biến nhất trong chứng minh toán học. Một ví dụ nổi tiếng của phương pháp này là chứng minh rằng $\sqrt{2}$ là một số vô tỷ.

Giả sử rằng $\sqrt{2}$ là một số hữu tỷ, thì có thể viết nó dưới dạng $\sqrt{2}=\frac{a}{b}$, với a và b là các số nguyên khác không, không có ước chung lớn hơn 1. Do đó, từ $b\sqrt{2}=a$, bình phương cả hai vế ta có 2b = a. Vì vế trái chia hết cho 2, nên vế phải cũng phải chia hết cho 2. Do đó, a là số chẵn, và a có thể viết dưới dạng 2c, với c là số nguyên. Thay vào phương trình ban đầu ta có 2b = (2c)^2 = 4c. Chia hai vế cho 2, ta có b = 2c, nên b cũng là số chẵn. Nếu cả a và b đều là số chẵn, thì chúng có chung ước số là 2, trái với giả thuyết ban đầu. Do đó, $\sqrt{2}$ không phải là số hữu tỷ.

Chứng minh bằng ví dụ cụ thể

Chứng minh bằng ví dụ cụ thể là phương pháp đưa ra một ví dụ cụ thể để chứng minh sự tồn tại của một đối tượng với thuộc tính mong muốn. Ví dụ, Joseph Liouville đã chứng minh sự tồn tại của số siêu việt bằng cách chỉ ra một ví dụ rõ ràng.

Chứng minh bằng cách kiểm tra từng trường hợp

Trong chứng minh bằng cách kiểm tra từng trường hợp, ta đạt được kết luận bằng cách phân chia vấn đề thành các trường hợp hữu hạn và chứng minh từng trường hợp riêng biệt. Số trường hợp có thể rất lớn. Ví dụ, chứng minh định lý bốn màu đầu tiên là một chứng minh bằng cách kiểm tra với 1.936 trường hợp. Phương pháp này còn gây tranh cãi vì nhiều trường hợp được kiểm tra bằng máy tính thay vì bằng tay. Phiên bản ngắn gọn nhất của chứng minh định lý bốn màu hiện nay vẫn có hơn 600 trường hợp.

Chứng minh xác suất

Chứng minh xác suất là phương pháp trong đó ta đưa ra một ví dụ để chứng minh sự tồn tại với một mức độ tin cậy nhất định, dựa trên các nguyên lý của lý thuyết xác suất. Cần phân biệt rõ với việc tranh luận về một định lý có thể đúng. Loại tranh luận này có thể gọi là 'tranh luận có vẻ đúng' và không phải là một chứng minh chính thức; điều này dễ thấy trong trường hợp phỏng đoán Collatz. Chứng minh xác suất, giống như chứng minh bằng ví dụ cụ thể, là một trong những phương pháp chứng minh sự tồn tại của định lý.

Chứng minh tổ hợp

Chứng minh tổ hợp chứng minh sự tương đương giữa các biểu diễn khác nhau bằng cách chỉ ra rằng chúng dẫn đến cùng một kết quả theo các cách khác nhau. Ví dụ, một phép ánh xạ song ánh giữa hai tập hợp thường được sử dụng để chứng minh rằng số lượng biểu thức trong chúng là như nhau.

Chứng minh không xây dựng

Một chứng minh không xây dựng (nonconstructive proof) chứng minh sự tồn tại của một đối tượng toán học nào đó (như 'Có một X sao cho f(X)'), mà không cung cấp cách tìm kiếm đối tượng đó. Thường, phương pháp này giống như chứng minh phản chứng, trong đó ta chứng minh việc không tồn tại là không thể xảy ra. Ngược lại, chứng minh xây dựng (hay chứng minh bằng dẫn chứng) cung cấp phương pháp để xác định đối tượng đó. Một ví dụ điển hình về chứng minh không xây dựng là chứng minh sự tồn tại của hai số vô tỷ $a$ và $b$ sao cho $a^b$ là số hữu tỷ.

Hoặc ${\sqrt{2}}^{\sqrt{2}}$ có thể là một số hữu tỷ, và như vậy đã chứng minh xong (với $a=b=\sqrt{2}$), hoặc ${\sqrt{2}}^{\sqrt{2}}$ có thể là số vô tỷ, và ta có thể viết $a={\sqrt{2}}^{\sqrt{2}}$ và $b=\sqrt{2}$. Ta tính được ${\left({\sqrt{2}}^{\sqrt{2}}\right)}^{\sqrt{2}}={\sqrt{2}}^2=2$, là số hữu tỷ.

Chứng minh thống kê trong toán học thuần túy

Thuật ngữ 'chứng minh thống kê' có thể được sử dụng trong các lĩnh vực toán học thuần túy, như mật mã học, chuỗi hỗn loạn, và lý thuyết số xác suất và phân tích. Tuy nhiên, nó ít được sử dụng để chỉ một chứng minh chính thức trong lĩnh vực thống kê toán học.

Chứng minh với sự hỗ trợ của máy tính

Vào thế kỷ 20, người ta tin rằng mọi chứng minh đều có thể được xác nhận tính chính xác bởi một nhà toán học xuất sắc. Ngày nay, máy tính không chỉ được sử dụng để chứng minh các định lý mà còn thực hiện những phép toán quá phức tạp để con người hay nhóm người kiểm tra. Chứng minh định lý bốn màu đầu tiên là một ví dụ điển hình về chứng minh có sự hỗ trợ từ máy tính. Một số nhà toán học lo ngại rằng lỗi trong chương trình máy tính hoặc sai sót khi tính toán có thể đặt câu hỏi về tính chính xác của các chứng minh máy tính. Tuy nhiên, nguy cơ xảy ra lỗi có thể giảm bằng cách áp dụng kiểm tra trùng lặp và tự kiểm tra, cũng như phát triển nhiều phương pháp và chương trình độc lập.

Các khái niệm liên quan

Chứng minh bằng hình ảnh

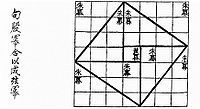
Dù không phải là phương pháp chứng minh chính thức, chứng minh bằng hình ảnh cho một định lý toán học đôi khi được gọi là 'chứng minh không cần lời'. Hình ảnh bên phải minh họa một chứng minh hình ảnh cổ xưa về định lý Pythagoras đối với tam giác (3, 4, 5).

Chứng minh sơ cấp

Chứng minh sơ cấp là những chứng minh chỉ dựa trên kiến thức cơ bản. Thuật ngữ này đặc biệt được sử dụng trong lý thuyết số để chỉ các chứng minh không cần đến phân tích số phức tạp. Mặc dù có quan điểm cho rằng một số định lý như định lý số nguyên tố chỉ có thể được chứng minh bằng phương pháp 'cao cấp', nhiều định lý đã được chứng minh lại bằng các kiến thức sơ cấp.

Chứng minh hai cột

Chứng minh hai cột là một phương pháp phổ biến trong các lớp học hình học cơ bản, trình bày dưới dạng hai cột song song. Trong đó, cột bên trái chứa các mệnh đề, còn cột bên phải giải thích ngắn gọn về tính chính xác của mệnh đề đó, như là một tiên đề, giả thuyết, hoặc kết quả từ dòng trước (hoặc đơn giản là 'suy diễn').

Các liên kết bên ngoài

• Các chứng minh toán học là gì và tại sao chúng quan trọng?
• 2πix.com: Logic Lưu trữ ngày 2009-09-08 tại Wayback Machine. Một phần của loạt bài viết về toán học và logic.
• Cách Viết Chứng Minh của Larry W. Cusick
• Cách Viết Chứng Minh của Leslie Lamport và động lực đề xuất kiểu chứng minh phân cấp như vậy.
• Chứng Minh Trong Toán Học: Đơn Giản, Quyến Rũ và Sai Lầm
• Các Chứng Minh của Thế Giới, biên tập bởi Freek Wiedijk, lời tựa bởi Dana S. Scott, Lecture Notes in Computer Science 3600, Springer, 2006, ISBN 3-540-30704-4. Chứa các phiên bản chính thức của chứng minh rằng $\sqrt{2}$ là số vô tỉ trong nhiều hệ thống chứng minh tự động.
• Chứng Minh Là Gì? Những suy nghĩ về chứng minh và việc chứng minh.
• ProofWiki.org Lưu trữ ngày 2012-07-31 tại Wayback Machine. Một tập hợp trực tuyến các chứng minh toán học.
• planetmath.org Một bách khoa toàn thư theo kiểu wiki về các chứng minh
• Một bài học về chứng minh, trong một khóa học từ Wikiversity