1. Các hệ thức lượng trong tam giác vuông - tập trung vào hệ thức liên quan đến cạnh và đường cao của tam giác vuông
Khái niệm và ứng dụng của tam giác vuông ΔABC trong chương trình lớp 9, cùng với ví dụ cụ thể và bài tập liên quan sẽ được trình bày chi tiết.
- Tam giác vuông ΔABC và các mối quan hệ quan trọng
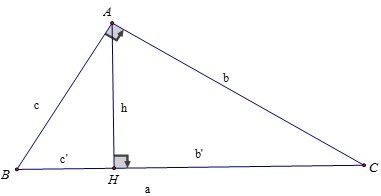
Trong chương trình đại số và hình học lớp 9, tam giác vuông ΔABC, hay còn gọi là tam giác vuông, là một khái niệm cốt yếu. Trong tam giác này, một góc được gọi là góc vuông và thường đặt tại đỉnh A. Hãy cùng tìm hiểu một số mối quan hệ quan trọng liên quan đến tam giác vuông này.
- Hình chiếu của các đoạn AB và AC trên cạnh BC
Trong tam giác vuông ΔABC, có hai đoạn thẳng đặc biệt, BH và CH, là hình chiếu của các đoạn AB và AC lên cạnh BC. Độ dài của BH và CH có thể được tính dựa trên các công thức sau:
+ Đoạn BH (c') được tính bằng cách nhân độ dài AB (c) với độ dài BC (a), với công thức: BH = c * a.
+ Đoạn CH (b' trong trường hợp này) được tính bằng cách nhân độ dài của AC (b) với độ dài BC (a), với công thức: CH = b * a.
- Các mối quan hệ giữa các đoạn thẳng trong tam giác
Chúng ta cũng có những mối quan hệ quan trọng sau đây:
+ Đoạn BH (c') và đoạn CH (b') liên quan đến độ dài đoạn AH (h) theo công thức: AH^2 = CH * BH, hoặc h^2 = b' * c'.
+ Mối quan hệ giữa các đoạn thẳng trong tam giác ΔABC: AB * AC = AH * BC, hay b * c = a * h.
- Định lý Pythagoras
Định lý Pythagoras là một trong những định lý quan trọng nhất trong hình học và đại số. Nó chứng minh rằng tổng bình phương của hai cạnh vuông góc (b và c) trong tam giác vuông bằng bình phương của cạnh huyền (a): AB^2 + AC^2 = BC^2, hay b^2 + c^2 = a^2.
Việc giải các bài tập và ví dụ thực tế liên quan đến tam giác vuông ΔABC giúp học sinh ứng dụng kiến thức vào thực tế và nâng cao hiểu biết về lĩnh vực này.
2. Hệ thức lượng trong tam giác vuông - chủ đề tỉ số lượng giác của góc nhọn
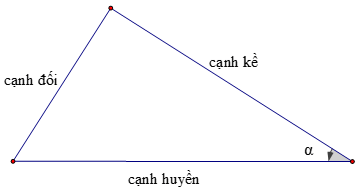

Mối liên hệ giữa các hàm lượng giác đóng vai trò quan trọng trong toán học và có ứng dụng đa dạng trong nhiều lĩnh vực. Hãy cùng phân tích sâu hơn về mối quan hệ này:
- Mối quan hệ cơ bản giữa các hàm lượng giác: Trong toán học, chúng ta thường nghiên cứu sự liên hệ giữa các hàm lượng giác trong tam giác vuông. Để hiểu rõ, hãy xem xét hai góc phụ nhau trong tam giác vuông.
Một góc và góc phụ của nó được thể hiện như sau:
+ Góc chính: θ
+ Góc phụ: (90° - θ)
Chúng ta có thể nhận thấy sự liên kết giữa các hàm lượng giác của góc chính (sin(θ), cos(θ), tan(θ)) và các hàm lượng giác của góc phụ (sin(90° - θ), cos(90° - θ), tan(90° - θ)) như sau:
+ Quan Hệ Giữa sin và cos: sin (θ) = cos(90° - θ)
+ Quan Hệ Giữa tan và cotan: tan(θ) = cot(90° - θ)
Những mối quan hệ này rất hữu ích khi cần tính toán các giá trị lượng giác cho các góc phụ nhau trong thực tế. Sử dụng các mối quan hệ này giúp chúng ta chuyển đổi các giá trị lượng giác nhanh chóng và thuận tiện.
- Một số hệ thức lượng cơ bản trong chương trình:
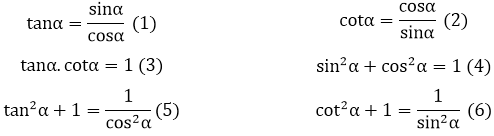
Trong toán học, việc so sánh các tỉ số lượng giác giữa các góc là một phần thiết yếu của hình học và đại số. Hãy cùng khám phá sâu hơn và phân tích các trường hợp sau đây:
- So sánh tỉ số lượng giác của hai góc nhọn α và β
Giả định rằng chúng ta có hai góc nhọn α và β, với α < β. Trong trường hợp này, chúng ta có các mối quan hệ quan trọng sau:
+ sin(α) < sin(β): Tỉ số sin của góc α nhỏ hơn tỉ số sin của góc β.
+ tan(α) < tan(β): Tỉ số tan của góc α nhỏ hơn tỉ số tan của góc β.
+ cos(α) > cos(β): Tỉ số cos của góc α lớn hơn tỉ số cos của góc β.
+ cot(α) > cot(β): Tỉ số cot của góc α lớn hơn tỉ số cot của góc β.
b) So sánh các tỉ số lượng giác của góc α
Chúng ta cũng có thể phân tích các tỉ số lượng giác của góc α một cách riêng biệt:
+ sin(α) < tan(α): Tỉ số sin của góc α nhỏ hơn tỉ số tan của góc α.
+ cos(α) < cot(α): Tỉ số cos của góc α nhỏ hơn tỉ số cot của góc α.
Những so sánh này giúp làm rõ mối liên hệ giữa các tỉ số lượng giác và sự tương tác của chúng trong các bài toán hình học và đại số. Kiến thức này rất quan trọng khi giải quyết các vấn đề liên quan đến góc và tỉ số lượng giác.
3. Hệ thức lượng trong tam giác vuông - chủ đề về mối quan hệ giữa góc và cạnh trong tam giác vuông
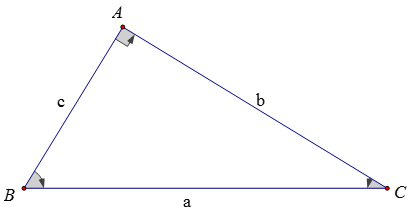
Tam giác vuông là một chủ đề quan trọng trong hình học với nhiều đặc điểm nổi bật. Chúng ta sẽ khám phá các hệ thức cơ bản trong tam giác vuông và mối liên hệ của chúng với các đại lượng cơ bản.
- Tỉ lệ giữa cạnh huyền và các cạnh còn lại
Trong tam giác vuông, có nhiều hệ thức quan trọng giữa cạnh huyền và các cạnh còn lại. Ví dụ, với một tam giác vuông có góc vuông tại đỉnh A, cạnh huyền là a, và hai cạnh kề là b và c. Ta có thể tính cạnh huyền (a) bằng cách nhân với sin của góc đối (sin B) hoặc cos của góc kề (cos C): a = b * sin(B) = c * cos(C).
- Các tỉ lệ giữa các cạnh và tỉ số lượng giác
Có những hệ thức quan trọng liên quan đến các cạnh và tỉ số lượng giác trong tam giác vuông. Ví dụ, trong tam giác vuông với góc vuông tại đỉnh A và hai cạnh kề b và c, các hệ thức sau đây giúp liên kết các đại lượng này:
+ Cạnh b có thể được tính bằng cách nhân cạnh huyền với tỉ số tan của góc đối (tan B) hoặc tỉ số cot của góc kề (cot C): b = a * tan(B) = c * cot(C)
+ Cạnh c có thể được tính bằng cách nhân cạnh huyền với tỉ số tan của góc đối (tan C) hoặc tỉ số cot của góc kề (cot B): c = a * tan(C) = b * cot(B)
Các hệ thức này giúp hiểu rõ sự tương tác giữa các đại lượng trong tam giác vuông, từ đó giải các bài toán hình học trở nên dễ dàng và hiệu quả hơn.
- Khi giải quyết bài toán về tam giác vuông, nhiệm vụ quan trọng là tìm ra tất cả thông tin còn thiếu trong tam giác, đặc biệt khi biết trước ít nhất hai yếu tố (trong đó có ít nhất một yếu tố về cạnh) và chưa biết các thông tin còn lại, bao gồm các góc và cạnh chưa được xác định.
Khi giải bài toán, chúng ta thường áp dụng các quy tắc hình học và tỉ số lượng giác để tìm các giá trị chưa biết. Cụ thể, có thể sử dụng các phương pháp sau:
+ Áp dụng tỉ số lượng giác: Nếu đã biết một cạnh và một tỉ số lượng giác (chẳng hạn a và sin(θ)), có thể tính các cạnh khác bằng cách dùng tỉ số lượng giác tương ứng. Ví dụ: b = a * tan(θ).
+ Sử dụng các quy tắc góc trong tam giác vuông: Khi đã biết một góc (không phải góc vuông) và một cạnh, chúng ta có thể dùng tỉ số lượng giác hoặc các quy tắc góc để tìm các thông tin còn lại.
Quá trình này yêu cầu sự khéo léo trong việc áp dụng kiến thức hình học và lượng giác, từ đó giúp giải quyết các bài toán tam giác vuông một cách chính xác và hiệu quả.
Bạn có thể tham khảo thêm: Các bài tập Toán 9 ôn thi vào lớp 10 được chọn lọc mới nhất. Cảm ơn bạn.
