1. Khái niệm về giá trị tuyệt đối
Giá trị tuyệt đối là một khái niệm quan trọng trong toán học và khoa học tính toán, thể hiện khoảng cách giữa các số thực trên trục số. Cụ thể, giá trị tuyệt đối của số a là khoảng cách từ a đến điểm 0 trên trục số, với a là số thực bất kỳ.
Hiểu rõ hơn: Giá trị tuyệt đối thể hiện khoảng cách giữa một số và điểm 0 trên trục số. Nếu số đó không âm (lớn hơn hoặc bằng 0), giá trị tuyệt đối của nó chính là số đó. Ngược lại, nếu số đó âm (nhỏ hơn 0), giá trị tuyệt đối của nó là số dương tương ứng, được tính bằng cách đổi dấu của số đó.
Ví dụ minh họa: Xem xét số -3 và 5 trên trục số, giá trị tuyệt đối của -3 là 3 (do đổi dấu), còn giá trị tuyệt đối của 5 là 5. Như vậy, giá trị tuyệt đối giúp xác định khoảng cách giữa các số, với kết quả luôn là số dương hoặc 0.
Các Tính Chất Toán Học Của Giá Trị Tuyệt Đối
Giá trị tuyệt đối là một khái niệm quan trọng trong toán học, với nhiều tính chất thú vị áp dụng cho mọi số thực. Chúng ta sẽ tìm hiểu chi tiết về những tính chất này để hiểu sự tương tác giữa các số và giá trị tuyệt đối của chúng.
- Tính chất 1: Không âm và Số 0. Một đặc điểm cơ bản của giá trị tuyệt đối là nó luôn không âm hoặc bằng 0. Cụ thể, với mọi số thực a, ta có: ∣a∣≥0
Ngoài ra, giá trị tuyệt đối của một số bằng 0 nếu và chỉ nếu số đó là 0: ∣a∣=0 ⇔ a=0
- Tính chất 2: Tính chất đẳng thức và bất đẳng thức. Giá trị tuyệt đối giúp phát triển tính chất đẳng thức và bất đẳng thức. Nếu giá trị tuyệt đối của một số khác 0, số đó cũng khác 0. Thêm vào đó, nếu hai số bằng nhau hoặc đối nhau, giá trị tuyệt đối của chúng cũng bằng nhau.
- Tính chất 3: Giới hạn dưới và giới hạn trên. Giá trị tuyệt đối có tính chất đặc biệt liên quan đến giới hạn dưới và giới hạn trên. Mọi số đều lớn hơn hoặc bằng giá trị tuyệt đối của nó, và đồng thời nhỏ hơn hoặc bằng giá trị tuyệt đối của nó.
- Tính chất 4: So sánh số âm. Trong hai số âm, số nào có giá trị tuyệt đối lớn hơn sẽ là số nhỏ hơn về mặt giá trị tuyệt đối. Ví dụ, với hai số thực âm a và b, nếu ∣a∣ > ∣b∣ thì a < b.
- Tính chất 5: So sánh số dương. Trong hai số dương, số nào nhỏ hơn thì giá trị tuyệt đối cũng nhỏ hơn. Ví dụ, với hai số thực dương x và y, nếu ∣x∣ < ∣y∣ thì x < y.
- Tính chất 6: Tích của giá trị tuyệt đối. Giá trị tuyệt đối của một tích bằng tích của giá trị tuyệt đối của các số thành phần. Cụ thể, với hai số thực a và b, ta có ∣a × b∣ = ∣a∣ × ∣b∣.
- Tính chất 7: Thương của giá trị tuyệt đối. Khi tính thương của hai số, giá trị tuyệt đối của thương bằng thương của giá trị tuyệt đối của chúng. Cụ thể, với hai số thực a và b, ta có: ∣a/b∣ = ∣a∣ / ∣b∣.
- Tính chất 8: Bình phương của giá trị tuyệt đối. Bình phương của giá trị tuyệt đối của một số tương đương với bình phương của chính số đó. Tức là, với mọi số thực a, ta có (∣a∣)² = a².
- Tính chất 9: Tổng hai giá trị tuyệt đối. Tổng của hai giá trị tuyệt đối luôn lớn hơn hoặc bằng giá trị tuyệt đối của tổng hai số đó. Kết quả bằng nhau khi hai số có cùng dấu. Cụ thể, với hai số thực a và b, ta có: ∣a∣ + ∣b∣ ≥ ∣a + b∣.
Các tính chất này giúp chúng ta hiểu sâu hơn về cách giá trị tuyệt đối tương tác với các số thực, là nền tảng cho nhiều phương pháp và ứng dụng trong toán học và khoa học. Giá trị tuyệt đối không chỉ là công cụ quan trọng trong toán học, mà còn giúp ta hiểu rõ hơn về các thuộc tính của số thực.
2. Các dạng bài tập giá trị tuyệt đối lớp 7
* Dạng 1:
Phân tích và giải phương trình |A(x)| = k. Đây là dạng phương trình phổ biến trong toán học và các môn khoa học tự nhiên. Để giải dạng phương trình này, cần cân nhắc các trường hợp sau:
- Trường hợp 1: k
- Trường hợp 2: k = 0. Khi k bằng 0, phương trình trở thành |A(x)| = 0. Điều này có nghĩa là giá trị tuyệt đối của A(x) phải bằng 0, và để giá trị tuyệt đối bằng 0 thì A(x) phải bằng 0: ∣A(x)∣ = 0 ⇒ A(x) = 0.
- Trường hợp 3: k > 0. Nếu k lớn hơn 0, phương trình là |A(x)| = k. Điều này chỉ ra rằng giá trị tuyệt đối của A(x) bằng k, và có hai trường hợp con xảy ra trong tình huống này:
+ A(x) = k, có nghĩa là A(x) bằng k.
+ A(x) = −k, tức là A(x) bằng âm k.
Phương trình |A(x)| = k có thể có nhiều nghiệm x trong trường hợp k > 0, tùy thuộc vào biểu thức cụ thể của A(x). Điều quan trọng là xác định các giá trị của x sao cho thỏa mãn phương trình trong mọi tình huống.
* Dạng 2:
Phương trình |A(x)| = B(x) và xử lý các tình huống đặc biệt. Đây là dạng phương trình phức tạp cần sự phân tích kỹ lưỡng. Chúng ta sẽ khám phá các bước giải quyết và các trường hợp đặc biệt liên quan.
- Bước 1: Xem xét trường hợp đặc biệt. Đầu tiên, cần kiểm tra tình huống khi B(x) là số âm. Trong trường hợp này, không có giá trị nào của x thỏa mãn phương trình vì giá trị tuyệt đối không bao giờ âm. Nếu B(x) < 0, phương trình không có nghiệm.
- Bước 2: Giải quyết phương trình chính. Tiếp theo, xử lý phương trình |A(x)| = B(x) khi B(x) không âm, tức là B(x) ≥ 0.
Chúng ta sẽ giải phương trình bằng cách phân tích các trường hợp dựa trên giá trị của A(x) và B(x). Cụ thể như sau:
+ Nếu
A(x) = B(x), tức là giá trị tuyệt đối của A(x) bằng B(x), ta tìm nghiệm cho x trong trường hợp này.
+ Nếu
A(x) = −B(x), tức là giá trị tuyệt đối của A(x) bằng âm B(x), ta tìm nghiệm cho x trong trường hợp này.
Các bước này sẽ giúp chúng ta tìm nghiệm cho phương trình |A(x)| = B(x) trong mọi tình huống, kể cả khi B(x) là số âm.
3. Bài tập chuyên đề giá trị tuyệt đối lớp 7
Bài 1: Xác định x, với điều kiện:
| a) |2x - 5| = 4 | b) 1/3 - |5/4 - 2x| = 1/4 | c) 1/2 - |x + 1/5| = 1/3 | d) 3/4 - |2x + 1| = 7/8 |
Bài 2: Tìm giá trị x, với điều kiện:
| a) 2|2x -3| = 1/2 | b) 7,5 - 3|5 - 2x| = -4,5 | c) |x + 4/15| - |-3,75| = -|-2,15| |
Bài 3: Tìm x, với điều kiện:
| a) 2|3x - 1| + 1 = 5 | b) |x/2 - 1| = 3 |
| c) |-x + 2/5| + 1/2 = 3,5 | d) |x - 1/3| = 2(3/5) |
Bài 4: Tìm giá trị x, với điều kiện:
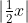
d) |7 - x| = 5x + 1
Bài 5: Tìm x, với điều kiện:
| a) l9 + xl = 2x | c) lx + 6l - 9 = 2x |
| b) l5xl - 3x = 2 | d) l2x - 3l + x = 21 |
Bạn đọc có thể tham khảo thêm: Đề thi học kỳ 1 môn Toán lớp 7 theo sách mới nhất với đáp án năm học 2023 - 2024. Cảm ơn bạn đã quan tâm!
