1. Lý thuyết về chuyên đề hình học lớp 5
1.1 Hình chữ nhật
Chu vi = (a+b) x 2
a + b = P / 2
Diện tích = a x b
a = P / 2 - b = S / b
b = P / 2 - a = S / a
Trong đó: S là diện tích; P là chu vi; a là chiều dài; b là chiều rộng.
1.2 Hình vuông
Chu vi = a x 4
Diện tích = a x a
a = P / 4
Trong đó: S là diện tích; P là chu vi; a là độ dài cạnh.
1.3 Hình bình hành
Chu vi = (a + b) x 2
a = P / 2 - b
Diện tích = a x h
h = S / a
(a + b) = P / 2
b = P / 2 - a
a = S / h
Trong đó: S là diện tích; P là chu vi; a là cạnh bên; b là cạnh đáy; h là chiều cao.
1.4 Hình thoi
P = a nhân 4
S = m nhân n: 2
a = P chia 4
m = 2 nhân S chia n
m nhân n = 2 nhân S n=2 nhân S chia m
1.5 Hình dạng tam giác
S = a nhân h chia 2
h = S nhân 2 chia a
a = S nhân 2 chia h
Trong đó: S là diện tích; a là đáy; h là chiều cao.
1.6 Hình thang
S = (a cộng b) nhân h chia 2
b = S nhân 2 chia h trừ a
a cộng b = S nhân 2 chia h
a = S nhân 2 chia h trừ b
h = S x 2: (a+b)
Trong đó: S là diện tích; a là cạnh lớn; b là cạnh nhỏ; h là chiều cao.
1.7 Hình tròn
C = d x 3,14 = r x 2 x 3,14
r = C: (3,14 x 2)
S = 1 x 1 x 3,14
1.8 Hình hộp chữ nhật
P đáy = (a + b) x 2
Sxq = P đáy x c
V = a x b x c
d = C: 3,14
r = d: 2
r x r = S: 3,14
S đáy = a x b
S tp = S xq + 2 x S đáy
P đáy = S xq : c
S đáy = V : c
Trong đó: a là chiều dài, b là chiều rộng, c là chiều cao; P là chu vi, S là diện tích, và V là thể tích
1.9 Hình lập phương
P đáy = a x 4
S đáy = a x a
Sxq = a x a x 4
Stp = a x a x 6
V = a x a x a
Trong đó: a là cạnh, P là chu vi, S là diện tích, và V là thể tích.
2. Các loại bài toán phổ biến trong chuyên đề hình học - Toán lớp 5
Có hai dạng chính khi giải quyết các bài toán về hình học phẳng và hình khối.
2.1 Dạng 1: Bài toán hình học phẳng
Dạng này bao gồm hai loại:
Các bài toán không liên quan đến tình huống thực tế, thường yêu cầu tính diện tích, chu vi hoặc một thuộc tính nào đó của hình vẽ được cho trong đề bài.
Các bài toán có tình huống thực tế, thường liên quan đến các khía cạnh trong đời sống hàng ngày.
Trong cả hai loại bài toán, chúng ta cần sử dụng và áp dụng các công thức tính chu vi và diện tích của các hình học phẳng đã học, như hình vuông, hình chữ nhật, tam giác, hình tròn, hình thang, và hình bình hành.
Bài tập minh họa
Bài 1: Tính diện tích của hình ngũ giác ABCDE theo kích thước đã cho trong hình.
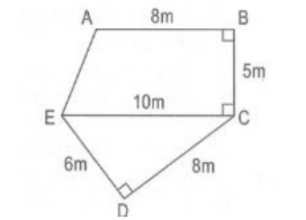
Để tính diện tích hình ngũ giác ABCDE, ta cộng diện tích của hình thang ABCE và hình tam giác ECD lại với nhau.
Diện tích hình thang ABCE được tính bằng công thức: (8 + 10) x 5 : 2 = 45 (m2)
Diện tích hình tam giác ECD được tính như sau: 6 x 8 : 2 = 24 (m2)
Vì vậy, diện tích tổng cộng của hình ngũ giác ABCDE là: 45 + 24 = 69 (m2)
Kết quả: 69m2
Bài 2: Một thửa đất hình thang có đáy lớn dài 120m, đáy nhỏ bằng 2/3 đáy lớn và dài hơn chiều cao 5m. Mỗi 100m2 thu hoạch được 72kg thóc. Tính tổng số thóc thu hoạch từ thửa đất đó.
Hướng dẫn cách giải:
+Sử dụng phương pháp tính phân số để xác định chiều dài đáy nhỏ.
+Tính chiều cao dựa vào chiều dài của đáy nhỏ.
+Tính diện tích của thửa đất hình thang.
+Tính tổng lượng thóc thu hoạch được.
Chiều dài đáy nhỏ là: 120 × 2/3 = 80 (m)
Chiều cao tính được là: 80 – 5 = 75 (m)
Diện tích của thửa ruộng được tính như sau:
(120 + 80) x 75 : 2 = 7500 (m2)
Số ki-lô-gam thóc thu hoạch từ thửa ruộng này là:
7500 chia cho 100 rồi nhân với 72 bằng 5400 (kg)
Kết quả là: 5400 kg thóc
2.2 Dạng 2: Bài toán về hình khối
Dạng bài này bao gồm các bài toán liên quan đến các hình khối như lập phương và hộp chữ nhật.
Để giải các bài toán dạng này, cần nắm vững cách tính diện tích bề mặt, diện tích toàn phần và thể tích của các hình khối.
Bài tập ví dụ
Bài 1: Tính thể tích của khối gỗ theo hình minh họa.
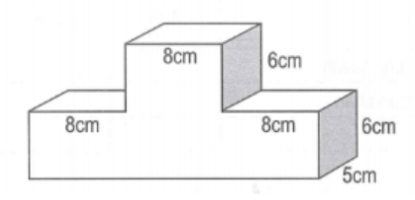
Hướng dẫn: Để xác định thể tích của khối gỗ, ta phân chia khối gỗ thành hai hình hộp chữ nhật nhỏ. Tính thể tích của từng hình hộp chữ nhật và cộng hai thể tích lại để có thể tích của khối gỗ.
Thể tích của từng hình hộp chữ nhật nhỏ là:
8 x 5 x 6 = 240 (cm³)
Thể tích của hình hộp chữ nhật nhỏ là:
(8 + 8 + 8) x 5 x 6 = 720 (cm³)
Tổng thể tích của khối gỗ là: 240 + 720 = 960 (cm³)
Kết quả: 960 cm³
Bài 2: Một thùng đựng hàng có nắp hình hộp chữ nhật với chiều dài 2,5m, chiều rộng 1,8m và chiều cao 2m. Cần bao nhiêu ki-lô-gam sơn để phủ toàn bộ bề mặt ngoài của thùng? Mỗi ki-lô-gam sơn có thể phủ được 5m2.
Hướng dẫn: Trước tiên, tính diện tích xung quanh và tổng diện tích của thùng hàng. Sau đó, tính toán lượng sơn cần thiết.
Diện tích xung quanh thùng hàng là:
(2,5 + 1,8) x 2 x 2 = 17,2 (m2)
Diện tích của hai đáy thùng hàng là:
2,5 x 1,8 x 2 = 9 (m2)
Tổng diện tích bề mặt của thùng đựng hàng là:
17,2 + 9 = 26,2 (m2)
Lượng sơn cần thiết là:
26,2 : 5 = 5,24 (kg)
Kết quả: 5,24kg
3. Bài tập ứng dụng hình học - Toán lớp 5
Bài 1: Một tấm bìa hình bình hành có chu vi 4 dm. Chiều dài lớn hơn chiều rộng 10 cm và bằng chiều cao. Tính diện tích của tấm bìa.
Bài 2: Một hình vuông có diện tích bằng 4/9 diện tích của một hình bình hành có đáy 25 cm và chiều cao 9 cm. Tính độ dài cạnh của hình vuông.
Bài 3: Một bể bơi có chiều dài 12 m, chiều rộng 5 m và sâu 2,75 m. Tính số viên gạch men cần dùng để lát đáy và xung quanh bể. Mỗi viên gạch có kích thước 25 cm x 20 cm và diện tích mạch vữa không đáng kể.
Bài 4: Một viên gạch hình hộp chữ nhật có kích thước 22 cm x 10 cm x 5,5 cm. Tính diện tích xung quanh và diện tích tổng của khối gạch được tạo thành từ 6 viên gạch xếp lại với nhau.
Bài 5: Để tạo ra 10 đoạn thẳng, cần tối thiểu bao nhiêu điểm?
Bài 6: Một tấm bìa hình bình hành có chu vi 4 dm. Chiều dài hơn chiều rộng 10 cm và bằng chiều cao. Tính diện tích của tấm bìa.
Bài 7: Sân trường của bạn có hình chữ nhật với chiều dài 45 m và chiều rộng 6,5 m. Có một bồn hoa hình tròn ở giữa sân với đường kính 3,2 m. Tính diện tích còn lại của sân trường.
Bài 8: Tính diện tích hình thang với đáy lớn là 25 m, chiều cao là 80% của đáy lớn, và đáy nhỏ là 90% của chiều cao.
Bài 9: Một miếng đất hình bình hành có đáy dài 32,5 m và chiều cao bằng 2/3 chiều dài đáy. Trên miếng đất này, mỗi mét vuông thu hoạch được 2,4 kg rau. Tính tổng khối lượng rau thu hoạch từ toàn bộ miếng đất.
Bài 10: Một miếng đất hình thoi có diện tích 288 m2 và một đường chéo dài 36 m. Miếng đất này được vẽ trên bản đồ với tỷ lệ 1:400. Tính diện tích của hình vẽ trên bản đồ.
Bài 11: Cho 5 điểm A, B, C, D, E, với điều kiện không có 3 điểm nào nằm trên cùng một đường thẳng. Khi nối các điểm này, sẽ có bao nhiêu đoạn thẳng được tạo ra?
