1. Cho ba đường thẳng phân biệt a, b, c. Biết a vuông góc với c, vậy b sẽ vuông góc với ai?
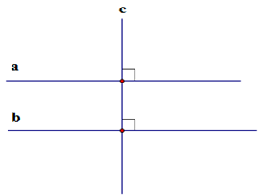
Câu hỏi: Cho ba đường thẳng phân biệt a, b, c với điều kiện a vuông góc với c và b cũng vuông góc với c. Vậy mối quan hệ giữa a và b là gì?
A. a song song với b
B. a cắt b
C. a vuông góc với b
D. Cả A, B, C đều không đúng
Giải thích chi tiết
Chúng ta có quy tắc: Nếu hai đường thẳng khác nhau đều vuông góc với một đường thẳng thứ ba, thì chúng sẽ song song với nhau.

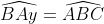
Đường d vuông góc với đường xy
Đường xy vuông góc với đường BC
Vậy đáp án chính xác là A
2. Câu hỏi liên quan
Câu 1: Hãy chọn phát biểu đúng từ các lựa chọn sau:
Một đường thẳng cắt hai đường thẳng phân biệt sẽ tạo ra
A. Hai góc so le trong bằng nhau
B. Hai góc đồng vị là bằng nhau
C. Hai góc đối đỉnh là bằng nhau
D. Hai góc so le ngoài là bằng nhau
Đáp án chính xác là C
Các đáp án A, B, D không đúng vì cần thêm điều kiện song song: Một đường thẳng cắt hai đường thẳng song song sẽ tạo ra các cặp góc so le trong, so le ngoài, đồng vị bằng nhau.
Đáp án C là chính xác vì hai đường thẳng cắt nhau tạo ra hai cặp góc đối đỉnh bằng nhau
Câu 2: Hãy chọn câu đúng. Hai góc đối đỉnh là:

B. Hai góc có một cạnh chung
C. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia

Đáp án chính xác là C
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia
Câu 3: Xác định giả thiết và kết luận của định lý sau: 'Nếu một đường thẳng c cắt hai đường thẳng a và b, và trong các góc tạo thành có một cặp góc so le trong bằng nhau, thì các cặp góc so le trong còn lại cũng bằng nhau'
A. Giả thiết: 'Có một cặp góc so le trong bằng nhau'; Kết luận: 'Hai góc so le trong còn lại cũng bằng nhau'
B. Giả thiết: 'Đường thẳng c cắt hai đường thẳng a và b, trong đó có một cặp góc so le trong bằng nhau'; Kết luận: 'Hai góc so le trong còn lại cũng bằng nhau'
C. Giả thiết: 'Đường thẳng c cắt hai đường thẳng a và b, tạo ra một cặp góc so le trong bằng nhau'; Kết luận: 'Hai góc đồng vị bằng nhau'
D. Giả thiết: 'Hai góc đồng vị bằng nhau'; Kết luận: 'Đường thẳng c cắt hai đường thẳng a và b, tạo ra một cặp góc so le trong bằng nhau'
Đáp án chính xác là B
Theo định lý: Giả thiết: 'Đường thẳng c cắt hai đường thẳng a và b, trong đó có một cặp góc so le trong bằng nhau'. Kết luận: 'Hai góc so le trong còn lại cũng bằng nhau'
Câu 4: Cho n (n > 1) đường thẳng phân biệt cắt nhau tại điểm O. Hỏi có bao nhiêu cặp góc đối đỉnh được hình thành?
A. n(n - 1)
B. n(n - 2)


Đáp án chính xác là A
Với n đường thẳng phân biệt giao nhau tại một điểm, tổng số tia chung gốc là 2n
Số góc được tạo ra từ các tia chung gốc là:
2n(2n - 1) / 2 = n(2n - 1)
Trong số đó có n góc bẹt. Số góc còn lại là:
n(2n - 1) - n = 2n(n - 1)
Do đó, số cặp góc đối đỉnh là n(n - 1)
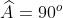
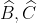
A. AI là đường cao của tam giác ABC
B. IB = IA = IC
C. AI là đường trung tuyến của tam giác ABC
D. ID = IE
Đáp án chính xác là D
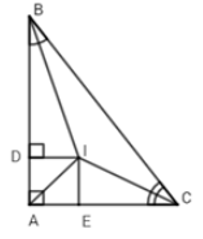
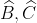
Do đó, ta loại A, B và C
Vì I là điểm giao của ba đường phân giác trong tam giác ABC nên
DI = IE (theo tính chất của ba đường phân giác trong tam giác)
Câu 6: Trong tam giác ABC cân tại A, trọng tâm là G và I là điểm giao của các đường phân giác. Khi đó, ta có:
A. I cách đều ba đỉnh của tam giác ABC
B. A, I, G nằm trên cùng một đường thẳng
C. G cách đều ba cạnh của tam giác ABC
D. Tất cả các đáp án trên đều đúng
Đáp án chính xác là B
I là điểm giao của các đường phân giác trong tam giác, do đó I cách đều ba cạnh của tam giác ABC. Loại bỏ đáp án A
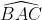
Câu 7: Trong tam giác ABC, hai đường phân giác CD và BE cắt nhau tại I. Khi đó
A. AI là trung tuyến từ đỉnh A
B. AI là đường cao từ đỉnh A
C. AI là đường trung trực của cạnh
D. AI là đường phân giác của góc
Đáp án chính xác là đáp án D
Vì hai đường phân giác CD và DE cắt nhau tại I và ba đường phân giác trong tam giác đều gặp nhau tại một điểm, nên AI là phân giác của góc A
Câu 8: Hãy chọn câu đúng nhất
A. Ba tia phân giác của một tam giác đều cắt nhau tại một điểm, gọi là trọng tâm của tam giác.
B. Điểm giao nhau của ba tia phân giác của tam giác cách đều ba cạnh của tam giác.
C. Trong một tam giác, đường trung tuyến từ một đỉnh có thể đồng thời là tia phân giác của cạnh đối diện.
D. Điểm giao nhau của ba tia phân giác trong tam giác là tâm của đường tròn ngoại tiếp tam giác.
Đáp án chính xác là đáp án B.
Vì trọng tâm là giao điểm của ba đường trung tuyến nên đáp án A không đúng. Loại bỏ đáp án A.
Giao điểm của ba đường phân giác trong tam giác cách đều ba cạnh của tam giác là chính xác.
Trong một tam giác, đường trung tuyến từ một đỉnh đồng thời là đường phân giác đối với cạnh đáy chỉ đúng khi tam giác cân tại đỉnh đó, vì vậy đáp án C sai.
Giao điểm của ba đường phân giác của tam giác không phải là tâm đường tròn ngoại tiếp, mà là tâm đường tròn nội tiếp.
3. Ôn lại lý thuyết
Mối liên hệ giữa tính vuông góc và tính song song của ba đường thẳng là: Nếu hai đường thẳng khác nhau đều vuông góc với một đường thẳng thứ ba, thì chúng sẽ song song với nhau.
- Mối liên hệ giữa tính vuông góc và tính song song của ba đường thẳng:
Hai đường thẳng khác nhau cùng vuông góc với một đường thẳng thứ ba sẽ song song với nhau.
a vuông góc với c; b cũng vuông góc với c
Kết luận: a song song với b
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song, thì nó cũng sẽ vuông góc với đường thẳng còn lại.
a song song với b; c vuông góc với a
Vì vậy: c vuông góc với b
Ba đường thẳng song song: Nếu hai đường thẳng khác nhau đều song song với một đường thẳng thứ ba, thì chúng sẽ song song với nhau.
a song song với c; b song song với c
Kết luận: a song song với b
Các loại bài toán thường gặp
Loại 1: Xác định hai đường thẳng song song hoặc vuông góc
Cách giải: Xem xét tính vuông góc và tính song song của hai đường thẳng so với một đường thẳng thứ ba:
- Nếu hai đường thẳng khác nhau đều vuông góc với một đường thẳng thứ ba, thì chúng sẽ song song với nhau
- Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song, thì nó cũng sẽ vuông góc với đường thẳng còn lại.
- Nếu hai đường thẳng khác nhau đều song song với một đường thẳng thứ ba, thì chúng sẽ song song với nhau.
Loại 2: Tính toán góc
Bước 1: Thêm một đường thẳng vào hình vẽ
Bước 2: Áp dụng các tính chất của hai đường thẳng song song, các góc kề bù, và các định lý liên quan.
Bài viết trên Mytour đã cung cấp thông tin chi tiết về ba đường thẳng phân biệt và các bài tập liên quan. Cảm ơn bạn đã theo dõi và đọc kỹ nội dung bài viết.
