| Phần của loạt bài |
| Cơ học lượng tử |
|---|
Phương trình Schrödinger |
|
|
Nền tảng[hiện] |
|
Nội dung cơ bản[hiện] |
|
Hiệu ứng[hiện] |
|
Thí nghiệm[hiện] |
|
Hàm số[hiện] |
|
Phương trình[hiện] |
|
Sự diễn giải[hiện] |
|
Chủ đề chuyên sâu[hiện] |
|
Nhà khoa học[hiện] |
Cơ học lượng tử (tiếng Anh: quantum mechanics) là lý thuyết nền tảng trong vật lý học mô tả các đặc tính của tự nhiên ở cấp độ nguyên tử hoặc hạt hạ nguyên tử. Đây là cơ sở cho các lý thuyết vật lý lượng tử như hóa học lượng tử, lý thuyết trường lượng tử, công nghệ lượng tử và khoa học thông tin lượng tử.
Vật lý cổ điển, bao gồm các lý thuyết được phát triển trước khi cơ học lượng tử ra đời, mô tả nhiều khía cạnh của tự nhiên ở quy mô vĩ mô, nhưng không phù hợp để giải thích các hiện tượng ở cấp độ vi mô (phân tử, nguyên tử và nhỏ hơn nguyên tử). Hầu hết các lý thuyết trong vật lý cổ điển có thể được suy ra từ cơ học lượng tử bằng cách xấp xỉ ở quy mô lớn.
Cơ học lượng tử khác biệt với cơ học cổ điển ở việc năng lượng, động lượng, mô men động lượng và các đại lượng khác của hệ đều nhận các giá trị rời rạc (lượng tử hóa); các thực thể có tính chất vừa là hạt vừa là sóng (lưỡng tính sóng-hạt); và có các giới hạn về khả năng xác định chính xác các đại lượng vật lý trước mỗi phép đo, dựa trên một tập hợp điều kiện ban đầu (nguyên lý bất định).
Cơ học lượng tử dần dần hình thành từ các lý thuyết giải thích các hiện tượng mà vật lý cổ điển không thể giải thích, như công trình của Max Planck năm 1900 về bức xạ vật đen, và bài báo năm 1905 của Albert Einstein về hiệu ứng quang điện. Những nỗ lực đầu tiên trong việc hiểu các hiện tượng vi mô, nay gọi là 'thuyết lượng tử cũ', đã dẫn đến sự phát triển hoàn thiện của cơ học lượng tử vào giữa thập niên 1920 bởi Niels Bohr, Erwin Schrödinger, Werner Heisenberg, Max Born và các nhà khoa học khác. Lý thuyết hiện đại được thể hiện qua nhiều mô hình toán học đặc trưng, trong đó có mô hình hàm sóng chứa thông tin về xác suất của các phép đo năng lượng, động lượng và các đặc tính vật lý khác của hạt.
Tổng quan và các khái niệm cơ bản
Cơ học lượng tử cho phép tính toán các tính chất và hành vi của các hệ thống vật lý, chủ yếu áp dụng cho các hệ thống vi mô như phân tử, nguyên tử và hạt hạ nguyên tử. Nó đã chứng minh khả năng mô tả chính xác các phân tử phức tạp với hàng nghìn nguyên tử, nhưng khi áp dụng cho con người, nó dẫn đến các vấn đề triết học, chẳng hạn như thí nghiệm tưởng tượng của Wigner, và đối với toàn vũ trụ vẫn chỉ là suy đoán. Các dự đoán của cơ học lượng tử đã được kiểm chứng thực nghiệm với độ chính xác rất cao.
Một đặc điểm cơ bản của lý thuyết là nó không thể đưa ra dự đoán chính xác về kết quả mà chỉ đưa ra xác suất cho từng khả năng. Về mặt toán học, xác suất được tính bằng bình phương giá trị tuyệt đối của một số phức, gọi là biên độ xác suất. Quy tắc Born, được đặt theo tên nhà vật lý Max Born, cho phép tính xác suất. Ví dụ, một hạt lượng tử như electron có thể được mô tả bằng hàm sóng, với mỗi điểm trong không gian tương ứng với một biên độ xác suất. Áp dụng quy tắc Born cho các biên độ này sẽ cho một hàm mật độ xác suất về vị trí của electron khi thực hiện phép đo. Đây là mức độ chính xác tối đa của lý thuyết; nó không thể xác định chính xác vị trí của electron. Phương trình Schrödinger liên kết các biên độ xác suất tại một thời điểm với các biên độ xác suất tại một thời điểm khác.
Một hệ quả của các quy tắc toán học của cơ học lượng tử là sự cân bằng về khả năng dự đoán giữa các đại lượng có thể đo lường. Nguyên lý bất định nổi tiếng nhất cho rằng dù hạt lượng tử được chuẩn bị hay thí nghiệm được sắp xếp như thế nào, không thể đồng thời dự đoán chính xác kết quả phép đo vị trí và động lượng của hạt.
Một kết quả nổi bật của các quy tắc toán học trong cơ học lượng tử là hiện tượng giao thoa lượng tử, thường được mô phỏng qua thí nghiệm hai khe. Trong thí nghiệm này, một nguồn sáng như chùm tia laser chiếu qua hai khe hẹp song song trên một tấm chắn, và ánh sáng đi qua các khe được quan sát trên một màn đặt phía sau tấm. Hiện tượng giao thoa xảy ra do sóng ánh sáng qua hai khe kết hợp, tạo ra các vân sáng và tối trên màn – kết quả này không thể có được nếu ánh sáng chỉ là các hạt cổ điển. Tuy nhiên, trên màn chắn, ánh sáng luôn xuất hiện dưới dạng các hạt riêng lẻ thay vì sóng; hình ảnh giao thoa xuất hiện do mật độ thay đổi của các hạt va chạm vào màn. Nếu gắn các máy dò ngay sau các khe, mỗi photon sẽ đi qua chỉ một khe (như một hạt cổ điển) và không qua cả hai khe (như một sóng). Các thí nghiệm cũng cho thấy rằng các hạt sẽ không tạo ra vân giao thoa nếu máy dò ghi nhận chúng đi qua khe nào. Các thực thể nguyên tử khác, như electron, cũng thể hiện hành vi tương tự khi bắn qua hai khe hẹp. Đặc điểm này được gọi là lưỡng tính sóng-hạt.
Một hiện tượng trái ngược với trực giác khác do cơ học lượng tử dự đoán là sự xuyên hầm lượng tử: một hạt có thể vượt qua một hàng rào thế, ngay cả khi động năng của nó thấp hơn thế năng của hàng rào. Trong cơ học cổ điển, hiện tượng này không xảy ra. Sự xuyên hầm lượng tử có một số hệ quả quan trọng: chẳng hạn, nó giải thích hiện tượng phân rã phóng xạ, phản ứng tổng hợp hạt nhân trong các sao, và các ứng dụng như kính hiển vi quét xuyên hầm và diode tunnel.
Khi các hệ lượng tử tương tác, có thể xảy ra hiện tượng rối lượng tử: các thuộc tính của chúng trở nên liên kết chặt chẽ đến mức không thể mô tả tổng thể theo từng phần riêng lẻ. Erwin Schrödinger đã mô tả sự vướng víu là '... đặc điểm đặc trưng của cơ học lượng tử, điều tách biệt hoàn toàn khỏi các quan điểm cổ điển.' Rối lượng tử cho phép những tính chất phi thường như trong lý thuyết trò chơi giả lượng tử (quantum pseudo-telepathy), và là nguồn tài nguyên quý giá trong các giao thức truyền thông, chẳng hạn như phân bố chìa khóa lượng tử trong lý thuyết thông tin lượng tử. Ngược lại với quan niệm phổ biến, rối lượng tử không cho phép gửi tín hiệu nhanh hơn ánh sáng, như đã được định lý không thể liên lạc chứng minh.
Một khả năng khác được mở ra nhờ rối lượng tử là kiểm tra 'lý thuyết biến ẩn', những thuộc tính giả định cơ bản hơn các đại lượng được mô tả trong lý thuyết lượng tử, mà các hiểu biết liên quan có thể cho phép dự đoán chính xác hơn. Các kết quả quan trọng, đặc biệt là định lý Bell, đã chứng minh rằng các lý thuyết biến ẩn thực tế không tương thích với vật lý lượng tử. Theo định lý Bell, nếu tự nhiên thực sự tuân theo một lý thuyết biến ẩn cục bộ, kết quả của thí nghiệm Bell sẽ phải tuân theo các ràng buộc cụ thể có thể định lượng được. Nhiều thí nghiệm Bell đã được thực hiện với các hạt rối, và chúng đã cho kết quả không tương thích với các ràng buộc của lý thuyết biến ẩn cục bộ.
Để hiểu sâu các khái niệm này, cần phải có kiến thức về định nghĩa toán học liên quan; việc nắm bắt cơ học lượng tử đòi hỏi không chỉ làm quen với các phép toán trên số phức, mà còn hiểu đại số tuyến tính, phương trình vi phân, lý thuyết nhóm, và các chủ đề toán học nâng cao khác. Bài viết này sẽ trình bày một khuôn khổ toán học cho cơ học lượng tử và minh họa các ứng dụng của nó qua một số ví dụ hữu ích và đã được nghiên cứu.
Khung toán học
Trong hệ thống toán học chính xác của cơ học lượng tử, trạng thái của một hệ cơ học lượng tử được đại diện bởi một vectơ trong không gian Hilbert phức (có thể phân tách) . Vectơ này được chuẩn hóa bằng phép toán tích vô hướng của không gian Hilbert, nghĩa là nó thỏa mãn , và được xác định rõ bởi một số phức có mô đun bằng 1 (trạng thái toàn cục), tức là và biểu thị cùng một hệ vật lý. Nói cách khác, các trạng thái có thể được coi là các điểm trong không gian xạ ảnh của không gian Hilbert, hay còn gọi là không gian xạ ảnh phức. Cấu trúc chính xác của không gian Hilbert này phụ thuộc vào hệ – chẳng hạn, để miêu tả vị trí và xung lượng, không gian Hilbert là không gian hàm phức bình phương khả tích (square-integrable function) , trong khi không gian Hilbert cho spin của một proton đơn lẻ chỉ là không gian vectơ phức hai chiều với tích vô hướng thông thường.
Các đại lượng vật lý như vị trí, xung lượng, năng lượng, spin được biểu diễn bằng các toán tử tuyến tính Hermit (hay còn gọi là toán tử tự liên hợp) tác động lên không gian Hilbert. Một trạng thái lượng tử là một vectơ riêng của một đại lượng quan sát được, và trong trường hợp đó, nó được gọi là trạng thái riêng, với giá trị riêng tương ứng cho giá trị của đại lượng quan sát được trong trạng thái đó. Nói chung, một trạng thái lượng tử có thể là tổ hợp tuyến tính của các trạng thái riêng, hay gọi là chồng chập lượng tử. Khi đo một đại lượng quan sát được, kết quả đo là một trong các giá trị riêng của nó với xác suất được tính theo quy tắc Born: trong trường hợp đơn giản, giá trị riêng không suy biến, và xác suất được tính bởi , với là vectơ riêng tương ứng của nó. Trong trường hợp tổng quát, nếu giá trị riêng là suy biến, xác suất đo được tính bằng , với là toán tử dự đoán tương ứng cho giá trị riêng đó.
Khi thực hiện phép đo và thu được kết quả , trạng thái lượng tử sẽ sụp đổ thành nếu không có sự suy biến, hoặc thành trong trường hợp tổng quát. Điều này cho thấy xác suất trong cơ học lượng tử phụ thuộc vào sự tương tác của phép đo, và đây là một trong những khía cạnh gây tranh cãi trong cơ học lượng tử, được phản ánh trong cuộc tranh luận nổi tiếng giữa Bohr và Einstein. Các giải thích về cơ học lượng tử đã được phát triển để làm rõ vấn đề này, như là giải thích đa thế giới. Theo đó, khi hệ lượng tử tương tác với thiết bị đo, hàm sóng của nó bị vướng víu, làm cho hệ lượng tử không còn tồn tại như một thực thể độc lập nữa.
Sự thay đổi theo thời gian của một hệ lượng tử được miêu tả bằng phương trình Schrödinger:
Ở đây là toán tử Hamilton, đại diện cho tổng năng lượng của hệ, và là hằng số Planck thu gọn. Hằng số được sử dụng để đảm bảo rằng toán tử Hamilton trong cơ học lượng tử trở thành toán tử Hamilton cổ điển khi hệ lượng tử có thể được xấp xỉ bằng một hệ cổ điển, theo nguyên lý tương ứng.
Nghiệm của phương trình vi phân tuyến tính này là:
Toán tử được gọi là toán tử tiến triển thời gian, có tính chất quan trọng là tính đơn điệu. Sự thay đổi của hệ lượng tử theo thời gian là hoàn toàn xác định, nghĩa là nếu ta biết trạng thái lượng tử tại một thời điểm nào đó , thì ta có thể dự đoán chính xác trạng thái lượng tử vào bất kỳ thời điểm nào sau đó.

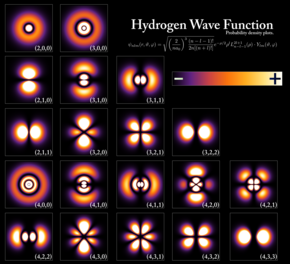
Có những hàm sóng có phân bố xác suất không thay đổi theo thời gian, như trạng thái riêng của Hamiltonian. Nhiều hệ trong cơ học cổ điển được mô tả bằng các hàm sóng tĩnh như vậy. Ví dụ, trong nguyên tử, electron trong trạng thái cơ bản được coi như là một hạt chuyển động tròn quanh hạt nhân theo cách cổ điển, trong khi trong cơ học lượng tử, nó được mô tả bằng một hàm sóng tĩnh (không phụ thuộc thời gian) bao quanh hạt nhân. Hàm sóng của electron trong nguyên tử hydro ở trạng thái cơ bản là một hàm đối xứng cầu, được gọi là orbital s (Xem Hình 1).
Các nghiệm chính xác của phương trình Schrödinger khá hiếm, chủ yếu là các nghiệm của những mô hình Hamilton đơn giản như dao động tử điều hòa lượng tử, hạt trong hộp, ion hydro phân tử và nguyên tử hydro. Ngay cả đối với nguyên tử heli, với chỉ hai electron, vẫn chưa có nghiệm chính xác mô tả hệ này.
Tuy nhiên, đã phát triển nhiều kỹ thuật để tìm nghiệm xấp xỉ. Một phương pháp được gọi là lý thuyết nhiễu loạn, sử dụng các nghiệm từ một mô hình cơ học lượng tử đơn giản để giải quyết các mô hình phức tạp hơn bằng cách thêm vào một thế năng nhỏ. Một phương pháp khác, được biết đến với tên gọi 'phương trình chuyển động bán cổ điển', áp dụng cho các hệ mà cơ học lượng tử chỉ tạo ra sự khác biệt nhỏ so với hệ cổ điển. Những khác biệt này có thể được tính toán từ các chuyển động cổ điển. Cách tiếp cận này rất quan trọng trong lý thuyết hỗn loạn lượng tử.
Nguyên lý bất định
Một hệ quả quan trọng của cơ học lượng tử là nguyên lý bất định. Nguyên lý này cho rằng không thể đồng thời dự đoán chính xác vị trí và động lượng của một hạt lượng tử. Cả vị trí và động lượng đều là những đại lượng quan sát được, tức là chúng được biểu diễn bằng các toán tử Hermit. Hai toán tử vị trí và toán tử xung lượng không giao hoán với nhau, nhưng chúng thoả mãn hệ thức giao hoán tử chính tắc:
Trong cơ học lượng tử, quy tắc Born cho phép tính các giá trị kỳ vọng cho cả và , cũng như các lũy thừa của chúng. Định nghĩa độ bất định của một biến quan sát được dựa trên độ lệch chuẩn, ta có:
Tương tự, đối với động lượng:
Nguyên lý bất định cho rằng
Theo nguyên tắc, mặc dù độ lệch chuẩn có thể được giảm đến mức rất nhỏ, nhưng không thể làm giảm đồng thời cả hai độ lệch chuẩn của một cặp toán tử tự liên hợp bất kỳ như và . Giao hoán tử giữa hai toán tử này được định nghĩa là:
và điều này thiết lập một giới hạn dưới cho tích của các độ lệch chuẩn:
Một hệ quả quan trọng từ định lý giao hoán tử là các toán tử vị trí và động lượng là các biến đổi Fourier của nhau. Điều này có nghĩa là mô tả về một hệ thống trong không gian động lượng tương ứng với biến đổi Fourier của mô tả trong không gian vị trí. Cụ thể, toán tử động lượng có thể được coi là tương đương với toán tử đạo hàm theo vị trí, kèm theo số hạng . Điều này giải thích tại sao trong các phương trình lượng tử trong không gian vị trí, toán tử động lượng được thay thế bằng , và đặc biệt trong phương trình Schrödinger không tương đối trong không gian vị trí, số hạng bình phương động lượng được thay thế bằng phép nhân với toán tử Laplace .
Hệ tổ hợp và trạng thái lượng tử
Khi nghiên cứu đồng thời hai hệ lượng tử khác nhau, không gian Hilbert của hệ tổ hợp được xác định bằng tích tensor của hai không gian Hilbert của các hệ thành phần. Ví dụ, giả sử A và B là hai hệ lượng tử với các không gian Hilbert và tương ứng. Khi đó, không gian Hilbert của hệ tổ hợp sẽ là:
Nếu trạng thái của hệ đầu tiên là vectơ và trạng thái của hệ thứ hai là , thì trạng thái của hệ tổ hợp sẽ là:
Tuy không phải mọi trạng thái trong không gian Hilbert liên hợp có thể được biểu diễn dưới dạng sản phẩm tensor, nguyên lý chồng chập cho thấy rằng các tổ hợp tuyến tính của các 'trạng thái phân tách' hay 'tách được' vẫn hợp lệ. Ví dụ, nếu và là các trạng thái khả dĩ của hệ , và tương tự và là các trạng thái khả dĩ của hệ , thì:
cũng là một trạng thái liên hợp khả dĩ nhưng không thể phân tách được. Những trạng thái không phân tách này được gọi là trạng thái vướng víu hay trạng thái rối lượng tử.
Khi một trạng thái của hệ tổ hợp là rối (hoặc không thể phân tách), không thể mô tả các hệ thành phần A hoặc B bằng một vectơ trạng thái đơn lẻ. Thay vào đó, ta cần sử dụng ma trận mật độ thu gọn để mô tả sự phân phối thống kê của các phép đo trên từng hệ thành phần. Tuy nhiên, các phép đo làm mất thông tin: việc biết ma trận mật độ thu gọn của từng hệ thành phần không đủ để khôi phục trạng thái của toàn bộ hệ tổ hợp. Tương tự như cách mà ma trận mật độ xác định trạng thái của một hệ trong một hệ lớn hơn, độ đo giá trị toán tử dương (POVM) mô tả ảnh hưởng của một phép đo trên một hệ thành phần từ một hệ lớn hơn. POVM thường được áp dụng trong lý thuyết thông tin lượng tử.
Như đã mô tả, vướng víu lượng tử là một đặc điểm quan trọng trong các quá trình đo, khi một thiết bị trở nên vướng víu với hệ được đo. Các hệ tương tác với môi trường của chúng thường bị vướng víu với môi trường, một hiện tượng được gọi là sự mất kết hợp lượng tử (quantum decoherence). Điều này giải thích tại sao các hiệu ứng lượng tử thường trở nên khó quan sát trong các hệ lớn hơn so với các hệ ở cấp độ vi mô.
Các hệ thống lý thuyết tương đương
Trong cơ học lượng tử, có nhiều hệ thống lý thuyết tương đương. Một trong những hệ thống lâu đời và phổ biến nhất là 'lý thuyết biến đổi' của Paul Dirac, lý thuyết này kết hợp và mở rộng hai hệ thống lý thuyết cơ bản của cơ học lượng tử: cơ học ma trận (do Werner Heisenberg, Max Born, và Pascual Jordan phát triển) và cơ học sóng (do Erwin Schrödinger phát triển). Một hệ thống lý thuyết khác là lý thuyết tích phân lộ trình của Feynman, trong đó biên độ xác suất được coi là tổng của tất cả các con đường khả dĩ cổ điển và phi cổ điển giữa trạng thái đầu và trạng thái cuối. Lý thuyết của Feynman được xem như là phiên bản tương đương của nguyên lý tác dụng trong cơ học cổ điển.
Các định luật bảo toàn và đối xứng
Toán tử Hamilton còn được gọi là toán tử tiến hóa, vì nó xác định toán tử tiến hóa theo thời gian unita cho mỗi giá trị của . Theo mối liên hệ giữa và , có thể thấy rằng mọi đại lượng quan sát được giao hoán với sẽ được bảo toàn: giá trị kỳ vọng của nó sẽ không thay đổi theo thời gian. Phát biểu này được tổng quát hóa bằng toán học rằng đối với bất kỳ toán tử Hermit nào, có thể xác định một họ các toán tử unita tham số hóa bởi biến . Trong sự tiến hóa bởi , bất kỳ đại lượng quan sát nào giao hoán với sẽ được bảo toàn. Hơn nữa, nếu bảo toàn trong sự tiến hóa dưới , thì sẽ được bảo toàn dưới sự tiến hóa do sinh ra. Điều này đồng nghĩa với phiên bản lượng tử của định lý Emmy Noether trong cơ học cổ điển (Lagrangian): với mỗi sự đối xứng khả vi của toán tử Hamilton, sẽ có một định luật bảo toàn tương ứng.
Minh họa
Hạt tự do

Hệ lượng tử cơ bản nhất với một bậc tự do vị trí là hạt tự do chuyển động trên một đường thẳng. Hạt này không bị ảnh hưởng bởi các yếu tố bên ngoài, do đó toán tử năng lượng Hamilton của nó chỉ chứa động năng.
Giải pháp tổng quát của phương trình Schrödinger được đưa ra bởi
hoặc là tổng hợp của tất cả các sóng phẳng khả dĩ , và cũng là các trạng thái riêng của toán tử xung lượng với xung lượng . Các hệ số chồng chập chính là , chính là biến đổi Fourier của trạng thái lượng tử ban đầu .
Không có nghiệm là trạng thái riêng của xung lượng hoặc vị trí riêng lẻ, vì những trạng thái này không thể chuẩn hóa được. Thay vào đó, chúng ta có thể xem xét một bó sóng Gauss:
với biến đổi Fourier, từ đó cho phép xác định phân bố xung lượng.
Khi ta thực hiện phân tán nhỏ hơn trong vị trí, sự phân tán trong xung lượng lại gia tăng. Ngược lại, nếu sử dụng bó sóng lớn hơn, sự phân tán trong xung lượng giảm, nhưng phân tán trong vị trí lại tăng. Điều này làm rõ nguyên lý bất định.
Khi bó sóng Gauss tiến triển theo thời gian, tâm của nó di chuyển trong không gian với tốc độ không thay đổi, giống như một hạt cổ điển không bị lực tác dụng. Tuy nhiên, bó sóng phân tán theo thời gian, dẫn đến sự bất định vị trí gia tăng, trong khi độ bất định xung lượng vẫn không đổi.
Hạt trong hộp
Hạt trong hộp thế năng một chiều là một ví dụ đơn giản về mặt toán học, nơi các ranh giới tạo ra sự lượng tử hóa các mức năng lượng. Hộp có thế năng bằng 0 ở khu vực bên trong, và thế năng vô hạn ở khu vực bên ngoài. Trong trường hợp một chiều theo hướng , phương trình Schrödinger không phụ thuộc thời gian có dạng
Với toán tử đạo hàm xác định bởi
phương trình trên tương tự như phương trình cho động năng cổ điển,
trạng thái trong trường hợp này có năng lượng tương đương với động năng của hạt.
Nghiệm tổng quát của phương trình Schrödinger cho hạt trong hộp có dạng
hoặc dưới dạng công thức Euler,
Trong một hộp vô hạn, các giá trị của và được xác định tại và , với phải bằng 0. Do đó, tại ,
và vì vậy . Ở ,
Trong đó không thể bằng 0, vì điều này sẽ mâu thuẫn với giả thuyết rằng có chuẩn bằng 1. Do đó, từ , cần phải là số nguyên bội của , hoặc
Ràng buộc này dẫn đến các mức năng lượng cần phải tuân theo điều kiện
Giếng thế hữu hạn là dạng tổng quát của bài toán giếng thế vô hạn nhưng dành cho trường hợp giếng thế có độ sâu hữu hạn. Về mặt toán học, bài toán giếng thế hữu hạn phức tạp hơn so với giếng thế vô hạn vì hàm sóng không triệt tiêu ở các bức tường của giếng thế. Thay vào đó, hàm sóng cần phải thỏa mãn các điều kiện biên phức tạp hơn khi nó không bằng 0 ở ngoài giếng thế. Các bài toán liên quan khác bao gồm rào thế hình vuông, một mô hình thể hiện hiệu ứng xuyên hầm lượng tử, có vai trò quan trọng trong các công nghệ hiện đại như bộ nhớ flash và kính hiển vi quét xuyên hầm.
Dao động của hệ điều hòa
Tương tự như trong cơ học cổ điển, thế của dao động tử điều hòa lượng tử được biểu diễn bởi
Bài toán này có thể được giải trực tiếp từ phương trình Schrödinger, một phương trình không đơn giản, hoặc sử dụng phương pháp bậc thang đơn giản hơn do Paul Dirac đề xuất lần đầu. Các trạng thái riêng được xác định bởi
với Hn là các đa thức Hermite
và các mức năng lượng tương ứng là
Đây là một ví dụ khác thể hiện sự phân tách của các mức năng lượng trong các trạng thái bị giới hạn.
Giao thoa kế Mach–Zehnder
Giao thoa kế Mach–Zehnder (MZI) minh họa các khái niệm giao thoa và chồng chập qua đại số tuyến tính trong không gian hai chiều, thay vì thông qua các phương trình vi phân. Có thể xem giao thoa kế như một phiên bản đơn giản của thí nghiệm hai khe, nhưng nó cũng có những điểm đặc biệt như trong thí nghiệm bộ xóa lượng tử lựa chọn trễ (delayed choice quantum eraser), thí nghiệm tưởng tượng kiểm tra hoạt động của bom bởi Elitzur–Vaidman (Elitzur–Vaidman bomb tester), và các nghiên cứu về vướng víu lượng tử.
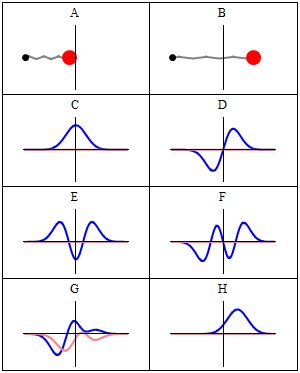
Chúng ta có thể hình dung một photon di chuyển qua giao thoa kế bằng cách xem xét rằng tại mỗi điểm, photon có thể nằm trong sự chồng chập của hai con đường: con đường 'dưới' bắt đầu từ bên trái, đi thẳng qua bộ tách chùm tia và kết thúc ở phía trên, và con đường 'trên' bắt đầu từ dưới, đi thẳng qua bộ tách chùm tia và kết thúc ở bên phải. Trạng thái lượng tử của photon có thể được biểu diễn bằng một vectơ là sự chồng chập của con đường 'dưới' và con đường 'trên' , tức là, với các số phức . Để đảm bảo điều kiện chuẩn hóa , hai số phức phải thỏa mãn .
Cả hai gương bán mạ được mô hình hóa bằng ma trận unita , có nghĩa là khi một photon gặp một gương bán mạ, nó sẽ ở trong cùng một con đường với xác suất biên độ , hoặc chênh lệch pha so với con đường khác.
Ma trận phản xạ là ma trận phản xạ đơn vị. Khi photon gặp ma trận phản xạ, photon sẽ bị phản xạ lại và chuyển từ con đường này sang con đường kia, thay vì thay đổi pha như với ma trận unita.
Xác suất để photon được phát hiện bên phải hoặc phía trên là
Do đó, ta có thể sử dụng giao thoa kế Mach–Zehnder để ước lượng sự dịch chuyển pha bằng cách tính toán các xác suất này.
Có điều thú vị khi xem xét tình huống nếu photon chắc chắn đi theo đường 'dưới' hoặc 'trên' giữa các gương bán mạ. Điều này có thể thực hiện bằng cách che chắn một đường, hoặc tương đương là loại bỏ một gương bán mạ (và chiếu photon từ trái hoặc dưới tùy ý). Trong cả hai trường hợp, không còn giao thoa giữa hai đường đi nữa, và các xác suất sẽ là , không phụ thuộc vào sự dịch chuyển pha của ánh sáng. Nếu có thêm thông tin về quá trình photon đi qua, chúng ta không thể ước lượng pha dựa vào phân phối xác suất đo được.
Các ứng dụng
Cơ học lượng tử đã đạt được thành tựu đáng kể trong việc giải thích nhiều đặc điểm của vũ trụ, tập trung vào các phạm vi nhỏ, các đại lượng rời rạc, và các tương tác không thể lý giải bằng các phương pháp cổ điển. Lý thuyết này chủ yếu mô tả hành vi của các hạt hạ nguyên tử, bao gồm electron, proton, neutron, photon, và các loại hạt khác. Cơ học lượng tử là nền tảng cho vật lý trạng thái rắn và khoa học vật liệu.
Trong nhiều lĩnh vực, công nghệ hiện đại hoạt động trong những phạm vi mà các hiệu ứng lượng tử trở nên quan trọng. Những ứng dụng chủ yếu của lý thuyết lượng tử bao gồm hóa học lượng tử, quang học lượng tử, tính toán lượng tử, nam châm siêu dẫn, diode phát quang, khuếch đại quang học và laser, transistor và chất bán dẫn như vi xử lý, cũng như các công cụ nghiên cứu và y học như chụp cộng hưởng từ và kính hiển vi điện tử. Nhiều hiện tượng vật lý và sinh học đều có thể được giải thích dựa trên bản chất của liên kết hóa học, nổi bật nhất là đại phân tử DNA.
Liên hệ với các lý thuyết khoa học khác
| Vật lý hiện đại |
|---|
Phương trình Schrödinger |
| Lịch sử vật lý hiện đại |
|
Người khởi xướng[hiện] |
|
Các ngành[hiện] |
|
Khoa học gia[hiện] |
Cơ học cổ điển
Các quy tắc cơ học lượng tử khẳng định rằng không gian trạng thái của một hệ là một không gian Hilbert và các đại lượng quan sát được là các toán tử Hermit tác dụng lên các vectơ trong không gian đó, mặc dù chúng không chỉ rõ không gian Hilbert nào hay toán tử nào. Việc chọn lựa không gian Hilbert và toán tử phù hợp là cần thiết để có được mô tả định lượng của hệ lượng tử, từ đó đưa ra dự đoán vật lý. Nguyên lý tương ứng là một hướng dẫn quan trọng, cho rằng các dự đoán của cơ học lượng tử sẽ chuyển thành mô tả cơ học cổ điển khi các số lượng tử lớn. Một cách tiếp cận khác là bắt đầu với một mô hình cổ điển và tìm mô hình lượng tử phù hợp để có thể tái hiện mô hình cổ điển trong giới hạn tương ứng. Đây được gọi là sự lượng tử hóa.
Khi cơ học lượng tử được thiết lập lần đầu, nó được áp dụng cho các mô hình mà trong giới hạn tương ứng là các mô hình cơ học cổ điển không tương đối tính. Ví dụ, mô hình dao động tử điều hòa lượng tử sử dụng một biểu thức phi tương đối tính để biểu diễn động năng của dao động tử, và do đó là phiên bản lượng tử của dao động tử điều hòa cổ điển.
Các hệ thống nhiễu loạn phức tạp hơn, khi không có các số lượng tử rõ ràng để mô tả, và lý thuyết nhiễu loạn lượng tử nghiên cứu sự liên hệ giữa các mô tả cổ điển và lượng tử trong các hệ này.
Sự mất kết hợp lượng tử là cơ chế qua đó các hệ lượng tử mất đi tính kết hợp, dẫn đến việc không thể hiện nhiều hiệu ứng lượng tử: sự chồng chập lượng tử chỉ còn là sự trộn lẫn các xác suất, và vướng víu lượng tử trở thành các tương quan cổ điển đơn giản. Sự kết hợp lượng tử thường không xuất hiện ở quy mô vĩ mô, trừ khi ở các mức nhiệt độ gần với độ không tuyệt đối, nơi các hành vi lượng tử thể hiện rõ rệt hơn.
Nhiều tính chất vĩ mô của hệ cổ điển là hệ quả trực tiếp của hành vi lượng tử của từng thành phần của nó. Ví dụ, sự ổn định của một khối vật chất (chứa các nguyên tử và phân tử có thể nhanh chóng phân rã dưới lực điện), tính cứng của vật rắn, và các tính chất cơ học, nhiệt, hóa học, quang học, và từ học của vật chất đều là kết quả của tương tác giữa các điện tích theo các quy tắc cơ học lượng tử.
Thuyết tương đối hẹp và điện động lực học
Những nỗ lực ban đầu để kết hợp cơ học lượng tử với thuyết tương đối hẹp bao gồm việc thay thế phương trình Schrödinger bằng các phương trình hiệp biến như phương trình Klein–Gordon hoặc phương trình Dirac. Dù các lý thuyết này đã giải thích nhiều kết quả thực nghiệm, chúng vẫn còn thiếu sót do không tính đến sự sinh và hủy các cặp hạt tương đối tính. Một lý thuyết lượng tử tương đối tính hoàn chỉnh yêu cầu phát triển lý thuyết trường lượng tử, áp dụng lượng tử hóa cho một trường thay vì các hạt cố định. Lý thuyết trường lượng tử đầu tiên được hoàn thiện là điện động lực học lượng tử, cung cấp mô tả lượng tử toàn diện về tương tác điện từ. Điện động lực học lượng tử, cùng với thuyết tương đối rộng, là một trong những lý thuyết vật lý chính xác nhất.
Không cần thiết phải sử dụng toàn bộ lý thuyết trường lượng tử để mô tả các hệ thống điện động lực. Một cách tiếp cận đơn giản hơn, đã được sử dụng từ khi cơ học lượng tử ra đời, là coi các hạt mang điện như các đối tượng cơ học lượng tử chịu tác động bởi một trường điện từ cổ điển. Ví dụ, mô hình lượng tử cơ bản của nguyên tử hydro mô tả điện trường của nguyên tử hydro bằng thế Coulomb cổ điển. Cách tiếp cận 'bán cổ điển' này không còn hiệu quả khi các thăng giáng lượng tử trong trường điện từ trở nên quan trọng, như trong sự phát ra photon từ các hạt mang điện.
Các lý thuyết trường lượng tử cho lực hạt nhân mạnh và yếu cũng đã được phát triển. Lý thuyết trường lượng tử cho lực hạt nhân mạnh, gọi là sắc động lực học lượng tử, mô tả các tương tác giữa các hạt nhỏ hơn hạt nhân nguyên tử như quark và gluon. Lực hạt nhân yếu và lực điện từ đã được thống nhất thành một lý thuyết trường lượng tử duy nhất, gọi là thuyết điện yếu, phát triển bởi các nhà vật lý Abdus Salam, Sheldon Glashow và Steven Weinberg.
Liên hệ với thuyết tương đối tổng quát
Dù cả cơ học lượng tử và thuyết tương đối tổng quát đã được kiểm chứng nhiều lần với các thực nghiệm phức tạp và chi tiết, các khái niệm lý thuyết của chúng vẫn mâu thuẫn và việc kết hợp chúng thành một lý thuyết thống nhất vẫn là thách thức lớn. Trong nhiều lĩnh vực của vật lý hạt, ảnh hưởng của hấp dẫn rất nhỏ, nên việc thống nhất thuyết tương đối rộng và cơ học lượng tử không phải là vấn đề cấp bách trong ứng dụng thực tiễn. Tuy nhiên, việc xây dựng một lý thuyết hấp dẫn lượng tử chính xác vẫn là một câu hỏi quan trọng trong vũ trụ học và việc tìm kiếm một 'lý thuyết vạn vật' (TOE) hoàn chỉnh tiếp tục là mục tiêu lớn của vật lý thế kỷ 20 và 21. Thuyết TOE sẽ không chỉ kết hợp các mô hình của vật lý hạt hạ nguyên tử mà còn giải thích bốn lực tự nhiên từ một lực thống nhất hoặc một hiện tượng chung.
Một đề xuất nổi bật là lý thuyết dây, cho rằng các hạt điểm trong vật lý hạt được thay thế bằng các đối tượng một chiều gọi là dây. Lý thuyết dây mô tả cách các dây này lan truyền và tương tác trong không gian. Khi nhìn từ khoảng cách lớn hơn kích thước của dây, một dây sẽ trông giống như một hạt cơ bản bình thường, với các thuộc tính như khối lượng và điện tích được xác định bởi các trạng thái rung động của nó. Trong lý thuyết dây, một trong những trạng thái rung động của dây tương ứng với hạt graviton, hạt lượng tử chịu trách nhiệm cho lực hấp dẫn.
Một lý thuyết phổ biến khác là hấp dẫn lượng tử vòng (LQG), mô tả tính chất lượng tử của hấp dẫn cũng như cấu trúc không-thời gian lượng tử. LQG cố gắng kết hợp cơ học lượng tử chuẩn với thuyết tương đối rộng chuẩn. Lý thuyết này xem không gian như một tấm vải cực kỳ mịn được cấu thành từ các vòng khép kín hữu hạn gọi là mạng lưới spin. Sự phát triển của mạng lưới spin theo thời gian được gọi là bọt spin. Độ dài đặc trưng của bọt spin bằng độ dài Planck, khoảng 1,616×10⁻³⁵ mét, do đó các kích thước nhỏ hơn độ dài Planck không có ý nghĩa trong LQG.
Ý nghĩa triết học
| Vấn đề mở trong vật lý học: Liệu có lời giải thích nào về cơ học lượng tử đúng đắn hơn hay không? Làm thế nào mà sự mô tả lượng tử của thực tại, bao gồm các yếu tố như "sự chồng chập của các trạng thái" và "suy sập hàm sóng", có thể tái tạo lại thực tại mà chúng ta nhận thức? (các vấn đề mở khác trong vật lý học)
|
Kể từ khi xuất hiện, nhiều khía cạnh phản trực giác và kết quả của cơ học lượng tử đã gây ra các cuộc tranh luận triết học mạnh mẽ và nhiều cách giải thích khác nhau. Các tranh luận tập trung vào bản chất xác suất của cơ học lượng tử, khó khăn trong việc suy sụp hàm sóng, và các vấn đề đo lường liên quan, cùng với tính phi định xứ lượng tử. Có thể nói rằng sự đồng thuận duy nhất về những vấn đề này là sự thiếu đồng thuận. Richard Feynman từng phát biểu, 'Tôi nghĩ tôi có thể tự tin nói rằng không ai thực sự hiểu cơ học lượng tử.' Theo Steven Weinberg, 'Theo quan điểm của tôi, hiện nay không có cách giải thích nào hoàn toàn thỏa đáng về cơ học lượng tử.'
Quan điểm của Niels Bohr, Werner Heisenberg và các nhà vật lý khác thường được gọi chung là 'giải thích Copenhagen'. Theo các quan điểm này, bản chất xác suất của cơ học lượng tử không phải là một đặc điểm tạm thời sẽ được thay thế bởi một lý thuyết chính xác hơn, mà là sự từ bỏ khái niệm cổ điển về 'quan hệ nhân quả'. Bohr đặc biệt nhấn mạnh rằng bất kỳ ứng dụng cụ thể nào của cơ học lượng tử đều phải được tham chiếu đến cách sắp xếp thí nghiệm, do sự bổ sung của các bằng chứng thu được từ các tình huống thí nghiệm khác nhau. Cách giải thích Copenhagen vẫn giữ được sự phổ biến trong thế kỷ 21.
Albert Einstein, mặc dù là một trong những người sáng lập thuyết lượng tử, đã gặp khó khăn với lý thuyết này vì nó không tuân theo một số nguyên lý siêu hình như tính tất định và tính định xứ. Các cuộc trao đổi kéo dài giữa Einstein và Bohr về ý nghĩa và trạng thái của cơ học lượng tử, được gọi là tranh luận Bohr–Einstein, cho thấy sự bất đồng. Einstein tin rằng dưới cơ học lượng tử phải có một lý thuyết không cho phép tác động từ xa. Ông xem cơ học lượng tử là lý thuyết chưa hoàn chỉnh, tương tự như nhiệt động lực học mà lý thuyết cơ bản là cơ học thống kê. Vào năm 1935, Einstein và các đồng sự Boris Podolsky và Nathan Rosen đã đưa ra lập luận cho rằng nguyên lý định xứ chỉ ra sự không hoàn chỉnh của cơ học lượng tử, dẫn đến thí nghiệm tưởng tượng được gọi là nghịch lý Einstein–Podolsky–Rosen. Năm 1964, John Bell chỉ ra rằng nguyên lý định xứ và thuyết tất định không tương thích với cơ học lượng tử, vì chúng dẫn đến các bất đẳng thức Bell mà các thí nghiệm thực tế đã chứng minh là có thể bị vi phạm bởi các hạt vướng víu. Điều này bác bỏ sự kết hợp giữa tính định xứ và thuyết tất định.
Lý thuyết De Broglie–Bohm cho thấy có thể điều chỉnh hình thức luận của cơ học lượng tử sao cho phù hợp với thuyết tất định, nhưng với điều kiện lý thuyết thể hiện rõ tính phi định xứ. Nó không chỉ gán một hàm sóng cho hệ thống vật lý mà còn cho một vị trí cụ thể, tiến triển một cách xác định theo một phương trình hướng dẫn phi cục bộ. Sự tiến triển của hệ thống vật lý được mô tả bằng phương trình Schrödinger kết hợp với phương trình hướng dẫn, vì vậy không có sự suy sụp của hàm sóng. Điều này giải quyết vấn đề đo lường.
Giải thích đa thế giới của Everett, ra đời năm 1956, cho rằng mọi xác suất được mô tả bởi cơ học lượng tử đều xuất hiện đồng thời trong một đa vũ trụ chứa các vũ trụ song song độc lập. Đây là hệ quả của việc loại bỏ tiên đề về sự suy sụp bó sóng. Mỗi trạng thái khả dĩ của hệ cùng với thiết bị đo và người quan sát đều tồn tại trong sự chồng chập lượng tử vật lý thực. Trong khi đa vũ trụ là tất định, chúng ta chỉ nhận thức hành vi phi tất định được chi phối bởi các xác suất vì chúng ta chỉ có thể quan sát một vũ trụ song song tại một thời điểm. Cách hoạt động chính xác của điều này đã là chủ đề của nhiều tranh luận. Một số nỗ lực đã được thực hiện để hiểu điều này và rút ra quy tắc Born, nhưng không có sự đồng thuận về việc liệu chúng có thành công hay không.
Cơ học lượng tử quan hệ xuất hiện vào cuối thập niên 1990 như một biến thể hiện đại của các ý tưởng kiểu Copenhagen, và QBism đã được phát triển vài năm sau đó.
Lịch sử
Cơ học lượng tử bắt đầu được phát triển vào những năm đầu thế kỷ 20, nhằm giải thích các hiện tượng đã được quan sát từ trước đó. Nghiên cứu về bản chất sóng của ánh sáng khởi đầu từ thế kỷ 17 và 18, khi các nhà khoa học như Robert Hooke, Christiaan Huygens và Leonhard Euler đề xuất lý thuyết sóng dựa trên quan sát thực nghiệm. Năm 1803, nhà khoa học Thomas Young thực hiện thí nghiệm hai khe nổi tiếng, đóng vai trò quan trọng trong việc xác nhận lý thuyết sóng của ánh sáng.
Vào đầu thế kỷ 19, nghiên cứu của John Dalton và Amedeo Avogadro đã củng cố thuyết nguyên tử của vật chất, một ý tưởng mà sau đó được James Clerk Maxwell, Ludwig Boltzmann và nhiều nhà khoa học khác phát triển thành thuyết động học chất khí. Những kết quả của thuyết động học đã làm sáng tỏ quan điểm rằng vật chất được cấu thành từ nguyên tử, tuy nhiên lý thuyết này vẫn còn thiếu sót và chỉ được giải quyết nhờ sự phát triển của cơ học lượng tử. Khái niệm nguyên tử từ triết học Hy Lạp mô tả chúng là các đơn vị không thể chia nhỏ – cụm từ 'nguyên tử' có nghĩa là 'không thể chia nhỏ' – nhưng thế kỷ 19 chứng kiến sự ra đời của các giả thuyết về cấu trúc hạ nguyên tử. Một thành tựu quan trọng là quan sát của Michael Faraday vào năm 1838 về lớp sáng tạo ra từ phóng điện trong ống thủy tinh chứa khí ở áp suất thấp. Công trình của Faraday được tiếp tục bởi Julius Plücker, Johann Wilhelm Hittorf và Eugen Goldstein, dẫn đến việc phát hiện tia âm cực và các hạt hạ nguyên tử, sau này được gọi là electron bởi J. J. Thomson.
Vấn đề bức xạ vật đen được Gustav Kirchhoff nghiên cứu vào năm 1859. Đến năm 1900, Max Planck đưa ra giả thuyết rằng năng lượng được bức xạ và hấp thụ dưới dạng các 'lượng tử' (hay gói năng lượng) rời rạc, phù hợp với các dạng bức xạ của vật đen quan sát được. Từ 'lượng tử' bắt nguồn từ tiếng Latinh, có nghĩa là 'lớn như thế nào' hoặc 'bao nhiêu'. Theo Planck, năng lượng có thể được chia thành các 'phần tử' với độ lớn (E) tỷ lệ với tần số (ν) của chúng:
- ,
với h là hằng số Planck. Planck đã cẩn trọng nhấn mạnh rằng đây chỉ là một khía cạnh của quá trình hấp thụ và phát xạ bức xạ, không phải là thực tại vật lý của bức xạ. Ông coi giả thuyết lượng tử của mình chủ yếu là một công cụ toán học để có kết quả chính xác hơn, chứ không phải một khám phá vĩ đại. Tuy nhiên, vào năm 1905, Albert Einstein đã giải thích giả thuyết lượng tử của Planck và áp dụng nó để giải thích hiệu ứng quang điện, trong đó ánh sáng chiếu vào một số vật liệu có thể làm bật electron ra khỏi vật liệu. Niels Bohr sau đó đã mở rộng ý tưởng của Planck về bức xạ để xây dựng mô hình nguyên tử hydro, dự đoán chính xác các vạch quang phổ của hydro. Einstein cũng phát triển thêm ý tưởng này để chứng minh rằng sóng điện từ như ánh sáng có thể được mô tả dưới dạng hạt (gọi là photon), với năng lượng rời rạc phụ thuộc vào tần số của nó. Trong bài báo 'Về lý thuyết lượng tử của bức xạ,' Einstein đã mở rộng mối liên hệ giữa năng lượng và vật chất để giải thích sự hấp thụ và phát xạ năng lượng của các nguyên tử. Dù thuyết tương đối rộng của ông đã làm lu mờ vấn đề này, bài báo đã làm sáng tỏ cơ chế cơ bản của sự phát xạ kích thích, nền tảng của công nghệ laser.
Giai đoạn này được gọi là thuyết lượng tử cũ. Không bao giờ hoàn chỉnh hoặc nhất quán, thuyết lượng tử cũ chủ yếu là các điều chỉnh heuristic đối với cơ học cổ điển. Hiện nay, lý thuyết này được coi là một phép gần đúng bán cổ điển của cơ học lượng tử hiện đại. Những kết quả đáng chú ý từ thời kỳ này bao gồm, ngoài công trình của Planck, Einstein và Bohr đã đề cập, công trình của Einstein và Peter Debye về nhiệt dung của chất rắn, chứng minh của Bohr và Hendrika Johanna van Leeuwen rằng vật lý cổ điển không giải thích được hiện tượng nghịch từ, và sự mở rộng của Arnold Sommerfeld đối với mô hình Bohr để bao gồm các hiệu ứng tương đối tính đặc biệt.

Vào giữa những năm 1920, cơ học lượng tử đã trở thành lý thuyết tiêu chuẩn cho vật lý nguyên tử. Năm 1923, nhà vật lý người Pháp Louis de Broglie đề xuất lý thuyết sóng vật chất, cho rằng các hạt có thể biểu hiện đặc tính sóng và ngược lại. Dựa trên lý thuyết của de Broglie, cơ học lượng tử hiện đại đã ra đời vào năm 1925, khi các nhà vật lý người Đức Werner Heisenberg, Max Born và Pascual Jordan phát triển cơ học ma trận, và nhà vật lý người Áo Erwin Schrödinger phát minh cơ học sóng. Born đã đưa ra cách giải thích xác suất cho hàm sóng Schrödinger vào tháng 7 năm 1926. Do đó, lĩnh vực vật lý lượng tử đã hình thành và được chấp nhận rộng rãi tại hội nghị Solvay lần thứ năm vào năm 1927.
Đến năm 1930, cơ học lượng tử đã được David Hilbert, Paul Dirac và John von Neumann hệ thống hóa và tinh chỉnh về mặt toán học, với sự chú trọng vào các phép đo, bản chất thống kê của hiểu biết về thực tại và các suy đoán triết học về 'người quan sát'. Kể từ đó, cơ học lượng tử đã lan rộng vào nhiều lĩnh vực như hóa học lượng tử, điện tử lượng tử, quang học lượng tử và khoa học thông tin lượng tử. Nó cũng cung cấp một nền tảng quan trọng cho nhiều đặc điểm của bảng tuần hoàn các nguyên tố hiện đại, mô tả hành vi của các nguyên tử trong quá trình liên kết hóa học và dòng electron trong chất bán dẫn máy tính, từ đó đóng vai trò thiết yếu trong nhiều công nghệ hiện đại. Dù được phát triển để mô tả thế giới vi mô, cơ học lượng tử cũng cần thiết để giải thích một số hiện tượng vĩ mô như chất siêu dẫn và siêu lỏng.
- Nguyên tử
- Hệ hai trạng thái lượng tử
- Vật lý lý thuyết
- Vật lý thực nghiệm
- Lịch sử vật lý học
Ghi chú
Khám phá thêm
Những tài liệu dưới đây được các nhà vật lý học biên soạn nhằm cung cấp thông tin về lý thuyết lượng tử cho độc giả không chuyên, với ít khái niệm kỹ thuật.
- Chester, Marvin (1987). Primer of Quantum Mechanics. John Wiley. ISBN 0-486-42878-8.
- Cox, Brian; Forshaw, Jeff (2011). The Quantum Universe: Everything That Can Happen Does Happen. Allen Lane. ISBN 978-1-84614-432-5.
- Feynman, Richard (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN 0-691-08388-6. Gồm bốn bài giảng cơ bản về điện động lực học lượng tử và lý thuyết trường lượng tử, tuy nhiên chứa nhiều thông tin chi tiết cho độc giả có chuyên môn.
- Ghirardi, Giancarlo (2004). Sneaking a Look at God's Cards. Gerald Malsbary biên dịch. Princeton University Press. ISBN 0-691-12139-7. Đây là tài liệu chuyên ngành cao nhất trong số các tài liệu trích dẫn. Có thể bỏ qua các đoạn liên quan đến đại số, lượng giác và ký hiệu bra–ket khi đọc lần đầu.
- Mermin, N. David (1990). “Spooky actions at a distance: mysteries of the quantum theory”. Boojums all the way through. Cambridge University Press. tr. 110–176. ISBN 0-521-38231-9.
- Stenger, Victor (2000). Timeless Reality: Symmetry, Simplicity, and Multiple Universes. Buffalo, NY: Prometheus Books. Chương 5–8. ISBN 1-57392-859-3. Bao gồm nghiên cứu về vũ trụ học và triết học.
Liên kết bên ngoài
- J. O'Connor và E.F. Robertson: Lịch sử của cơ học lượng tử.
- Giới thiệu về lý thuyết lượng tử tại Quantiki.
- Các video bài giảng của Hans Bethe về vật lý lượng tử đơn giản hóa: ba video bài giảng
- Tài liệu học tập
- Quantum Cook Book và PHYS 201: Các nguyên lý cơ bản của vật lý II của Ramamurti Shankar, Yale OpenCourseware
- Cách mạng hiện đại trong vật lý – sách giáo khoa trực tuyến.
- MIT OpenCourseWare: Hóa học và Vật lý. Xem 8.04, 8.05 và 8.06
- 5½ Ví dụ trong cơ học lượng tử
- Khoá học cơ học lượng tử của Imperial College.
- Triết học
- Ismael, Jenann. “Cơ học lượng tử”. Trong Zalta, Edward N. (biên tập). Stanford Encyclopedia of Philosophy.
- Krips, Henry. “Đo lường trong lý thuyết lượng tử”. Trong Zalta, Edward N. (biên tập). Stanford Encyclopedia of Philosophy.
- Sách Wikibooks (tiếng Anh)
- Thế giới lượng tử
Các ngành của vật lý học | |
|---|---|
| Phạm vi |
|
| Năng lượng, Chuyển động |
|
| Sóng và Trường |
|
Khoa học vật lý và Toán học |
|
Vật lý / Sinh học / Địa chất học / Kinh tế học |
|


| Tiêu đề chuẩn |
|
|---|
