Vũ trụ quá lớn và phức tạp, vì vậy hiện tại chúng ta vẫn không thể quan sát và đo lường nó trực tiếp được.
Vũ trụ có kích thước và cách chúng ta xa đến đâu? Đây có thể là những câu hỏi cơ bản và lâu đời nhất của loài người, đồng thời cũng là những câu hỏi mà các nhà khoa học đang nghiên cứu và cố gắng giải đáp.
Trả lời những câu hỏi này không dễ dàng. Vì vũ trụ quá lớn và phức tạp, nên chúng ta không thể quan sát và đo lường nó trực tiếp được.
Làm thế nào con người có thể biết kích thước và khoảng cách của vũ trụ? Làm sao chúng ta có thể tính toán vị trí và đặc điểm của các thiên hà và tinh vân cách xa hàng tỷ năm ánh sáng?
Để trả lời những câu hỏi này, chúng ta cần hiểu một khái niệm quan trọng: thang đo khoảng cách vũ trụ.

Hình ảnh minh họa. Ảnh: Thiên văn học
Dưới đây là một chuỗi các phương pháp và công cụ mà các nhà khoa học đã phát triển để đo vị trí và kích thước của các thiên thể ở các khoảng cách khác nhau trong vũ trụ. Những phương pháp và công cụ này tương tự như các bậc thang, giúp chúng ta khám phá vũ trụ sâu hơn mỗi ngày.
Tại sao chúng ta cần một bước như vậy? Bởi vì các thiên thể ở các khoảng cách khác nhau có đặc điểm và mẫu mã khác nhau, vì vậy chúng ta cần đo chúng bằng các phương pháp khác nhau.
Ví dụ, để đo khoảng cách giữa các hành tinh trong Hệ Mặt Trời, chúng ta có thể sử dụng sóng vô tuyến; đối với các ngôi sao ở xa hơn, chúng ta có thể sử dụng phương pháp thị sai lượng giác; và đối với các thiên hà cách xa, chúng ta có thể sử dụng siêu tân tinh hoặc định luật Hubble. Mỗi bước đo lường dựa trên kết quả của bước trước, tạo thành một hệ thống đáng tin cậy và nhất quán.

Hình minh họa. Ảnh: Thiên văn học
Phương pháp phản xạ vô tuyến
Phương pháp phản xạ vô tuyến sử dụng sóng vô tuyến truyền đến bề mặt của một hành tinh ở gần và đo thời gian để tín hiệu quay trở lại. Phương pháp này thích hợp cho các thiên thể trong Hệ Mặt Trời và được phát triển từ những năm 1950.
Trong những năm 1950, các nhà khoa học Mỹ đã sử dụng hệ thống radar quân sự để truyền sóng vô tuyến đến Mặt Trăng và đo thời gian để nhận tín hiệu phản xạ trở lại.
Sau đó, phương pháp này được áp dụng để đo khoảng cách giữa Trái Đất và các hành tinh khác như Sao Kim và Sao Hỏa, thậm chí cả các tiểu hành tinh và sao chổi. Ưu điểm của phép đo phản xạ vô tuyến là độ chính xác cực kỳ cao, cho phép đo sai số ở cấp độ milimet.
Điều này giúp các nhà khoa học hiểu chính xác hơn về khoảng cách và vị trí tương đối của các hành tinh. Tuy nhiên, phương pháp phản xạ vô tuyến cũng có một số hạn chế. Nó chỉ hoạt động trên các vật thể có bề mặt rắn, không hoạt động trên những vật thể có bầu khí quyển dày hoặc mây như Sao Mộc và Sao Thổ. Nguyên nhân là sóng vô tuyến bị tán xạ hoặc bị hấp thụ trong khí quyển, gây ra sai số trong việc đo thời gian của tín hiệu phản xạ.

Hình minh họa. Ảnh: Thiên văn học
Phương pháp thị sai lượng giác
Phương pháp thị sai lượng giác là một phương pháp đo cổ xưa và trực quan, sử dụng sự thay đổi vị trí của các ngôi sao trên bầu trời khi Trái Đất quay quanh Mặt Trời để tính góc giữa các ngôi sao và Trái Đất, từ đó suy ra khoảng cách của chúng.
Phương pháp này hiệu quả với những ngôi sao tương đối gần Trái Đất, thường trong phạm vi 100 năm ánh sáng. Dựa trên nguyên lý của phương pháp thị sai lượng giác, chúng ta có thể sử dụng các hình tam giác trong quan hệ hình học để giải các bài toán tìm độ dài các cạnh chưa biết.
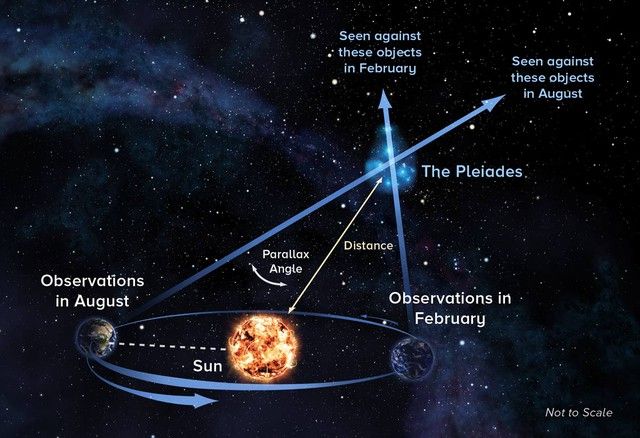
Hình minh họa. Ảnh: Thiên văn học
Vào đầu thế kỷ 19, nhà thiên văn học người Đức Friedrich Bissell đã thành công trong việc sử dụng phương pháp thị sai lượng giác để đo góc thị sai của ngôi sao 61 Pegasus và ước tính khoảng cách từ Trái Đất đến nó là 10,4 năm ánh sáng. Bước tiến này đã làm cho phương pháp thị sai lượng giác trở thành một công cụ quan trọng để đo khoảng cách đến các ngôi sao.
Sau đó, các nhà khoa học đã áp dụng phương pháp này để đo khoảng cách của nhiều ngôi sao khác, bao gồm cả ngôi sao gần Trái Đất nhất, Alpha Centauri, cách chúng ta 4,3 năm ánh sáng. Ưu điểm của phương pháp này là nó có thể được tính toán trực tiếp và đơn giản, không cần phụ thuộc vào các giả định hoặc mô hình khác. Tuy nhiên, nó chỉ hiệu quả đối với những ngôi sao gần Trái Đất. Đối với những ngôi sao ở xa hơn, góc thị sai trở nên rất nhỏ và khó đo chính xác.

Hình minh họa. Ảnh: Thiên văn học
Phương pháp đo khoảng cách bằng định luật Hubble
Định luật Hubble là một định luật quan trọng mô tả sự mở rộng của vũ trụ, dựa trên việc quan sát giá trị dịch chuyển đỏ của các vật thể ở xa. Phương pháp này có thể áp dụng cho các thiên hà rất xa, thậm chí cả chân trời sự kiện, có thể rộng đến hơn 10 tỷ năm ánh sáng. Định luật Hubble được nhà thiên văn học người Mỹ Edwin Hubble phát hiện và đề xuất vào những năm 1920.
Ông đã quan sát nhiều thiên hà ngoài thiên hà và phát hiện ra một sự thật đáng kinh ngạc: các thiên hà này đều đang rộng lớn ra xa chúng ta với các tốc độ khác nhau, và càng xa thì chúng càng chuyển động nhanh hơn.
Điều này cho thấy rằng vũ trụ không tĩnh tại mà thay vào đó, nó đang ngày càng mở rộng và phát triển. Định luật Hubble có thể được mô tả bằng một công thức đơn giản: v = H0d. Ở đây, v là tốc độ của các thiên hà ở xa, d là khoảng cách giữa chúng ta và thiên hà, và H0 là hằng số Hubble, miêu tả tốc độ mở rộng của vũ trụ. Dựa trên độ dịch chuyển đỏ của các thiên hà, chúng ta có thể xác định được tốc độ chúng đang rộng ra như thế nào.

Hình ảnh minh họa. Hình ảnh: Thiên văn học
Tiếp theo, bằng cách sử dụng định luật Hubble, chúng ta có thể tính được khoảng cách của các thiên hà xa xôi so với chúng ta. Một điều thu hút của định luật Hubble là khả năng đo lường những khoảng cách vô cùng xa mà thường không thể đo được. Hơn nữa, định luật Hubble dựa trên các đặc tính của toàn bộ vũ trụ chứ không chỉ riêng từng thiên thể. Điều này giúp chúng ta có thể nghiên cứu quy mô của vũ trụ một cách toàn diện hơn và hiểu được quá trình tiến hóa và cấu trúc của nó.
Tuy nhiên, định luật Hubble cũng có một số hạn chế. Trước hết, nó dựa vào sự chính xác và ổn định của hằng số Hubble. Hằng số này có thể biến đổi theo thời gian và không gian. Thứ hai, một số yếu tố như việc vũ trụ mở rộng nhanh chóng, năng lượng tối và vật chất tối cũng sẽ ảnh hưởng đến định luật Hubble.
Do đó, khi tiến hành các đo lường dựa trên định luật Hubble, chúng ta cần xem xét các yếu tố này và thực hiện các điều chỉnh phù hợp. Mặc dù định luật Hubble có một số hạn chế và thách thức, nhưng nó vẫn là một công cụ quan trọng giúp chúng ta hiểu biết về vũ trụ. Bằng cách liên tục cải thiện công nghệ quan sát và đo lường chính xác hằng số Hubble, chúng ta có thể khám phá sâu hơn những bí ẩn của vũ trụ và tiết lộ nguồn gốc, quá trình tiến hóa và tương lai của nó.
