Excel hỗ trợ tính toán hàm lượng giác một cách đơn giản và thuận tiện cho người sử dụng. Đặc biệt, trong những bài toán phức tạp, công cụ này mang lại sự hỗ trợ quan trọng. Dưới đây là giới thiệu về các hàm lượng giác mà Excel hỗ trợ.
1. Hàm Sin
- Cú Pháp: Sin (số).
Trong trường hợp này: số là giá trị độ của góc cần tính Sin.
- Ý Nghĩa: Trả về giá trị Sin của một góc, giá trị nằm trong khoảng từ -1 đến +1.
- Ví Dụ:
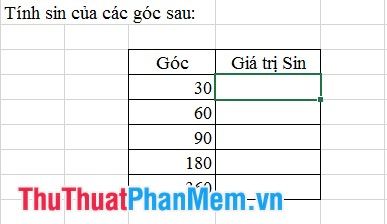
Chú ý: Khi làm việc với các hàm lượng giác trong Excel, đơn vị đo độ là radians.
Bước 1: Chuyển đơn vị đo độ sang radians. Thêm một cột mới và nhập lệnh như hình minh họa:

Bước 2: Áp dụng định dạng cho các ô còn lại. Sử dụng công thức tính giá trị Sin theo hình minh họa dưới đây:
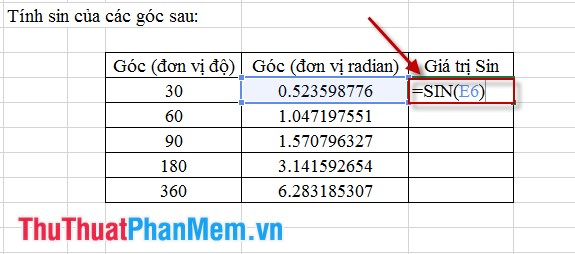
Cuối cùng, kéo định dạng cho các ô còn lại để có kết quả như trong hình sau:
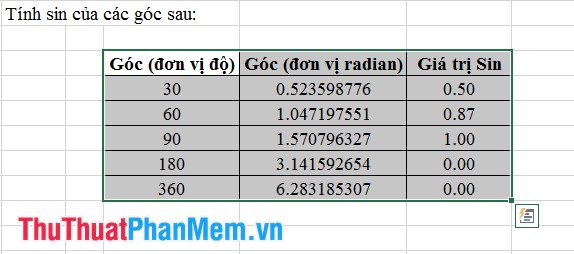
2. Hàm Cos
- Cú Pháp: Cos (số).
Trong trường hợp này: số là giá trị độ của góc cần tính Cos.
- Ý Nghĩa: Trả về giá trị Cos của một góc, giá trị nằm trong khoảng từ -1 đến +1.
- Ví Dụ:
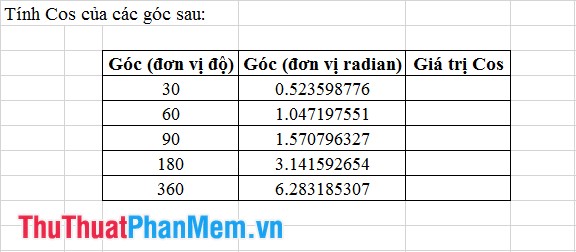
Bước 1: Nhập công thức theo hình minh họa.
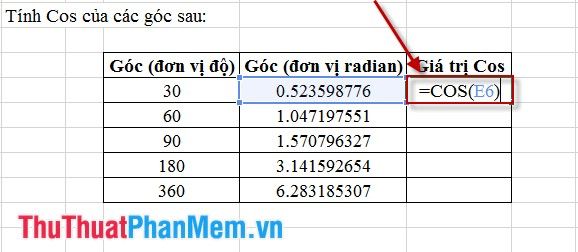
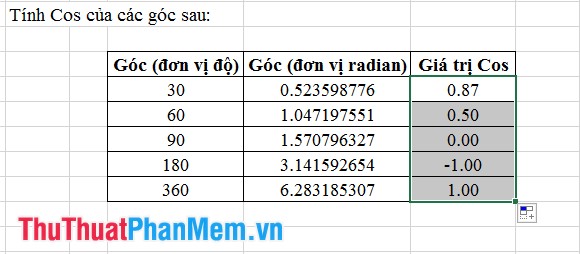
Bước 2: Áp dụng định dạng cho các ô còn lại để có kết quả như hình dưới đây:
3. Hàm Tan
- Cú Pháp: Tan (số).
Trong trường hợp này: số là giá trị độ của góc cần tính Tan.
- Ý Nghĩa: Trả về giá trị Tan của một góc, giá trị nằm trong khoảng từ -1 đến +1.
- Ví Dụ:
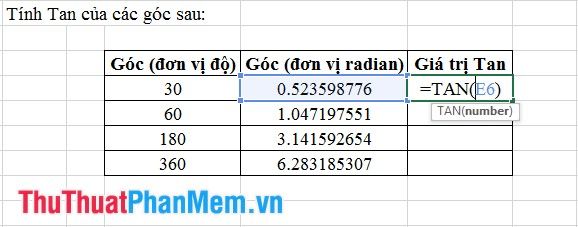
4. Hàm Asin
- Cú Pháp: Asin (số).
Trong trường hợp này: số là giá trị độ của góc cần tính Asin.
- Ý Nghĩa: Trả về giá trị Asin của một góc, giá trị nằm trong khoảng từ -1 đến +1.
- Ví Dụ:
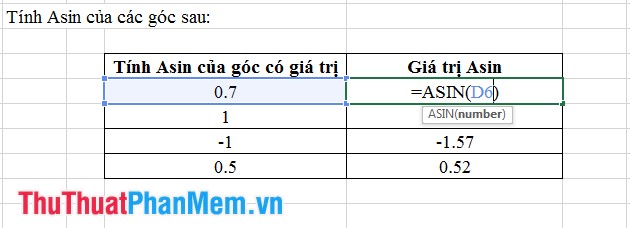
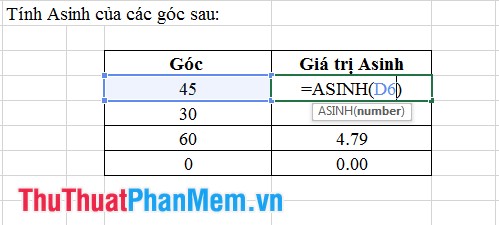
5. Hàm Asinh
- Cú Pháp: Asinh (số).
Trong trường hợp này: số là giá trị độ của góc cần tính Asin.
- Ý Nghĩa: Trả về giá trị Asinh của một góc, nhưng giá trị này được tính bằng radian.
- Ví Dụ:
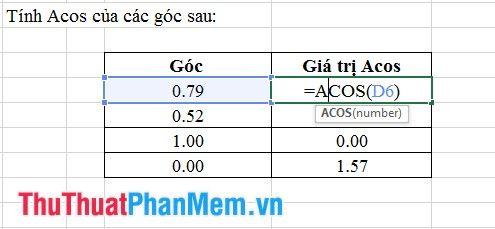
6. Hàm Acos
- Cú Pháp: Acos (số).
Trong trường hợp này: số là giá trị độ của góc cần tính Acos.
- Ý Nghĩa: Trả về giá trị Acos của một góc, giá trị nằm trong khoảng từ -1 đến +1.
- Ví Dụ:
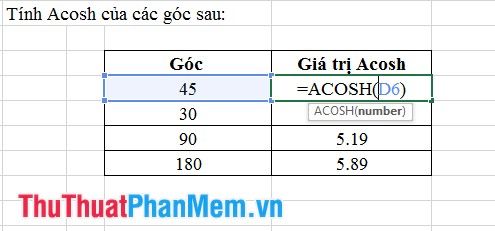
7. Hàm Acosh
- Cú Pháp: Asinh (số).
Trong trường hợp này: số là giá trị của góc cần tính Acosh.
- Ý Nghĩa: Trả về giá trị Acosh của một góc, nhưng giá trị này được tính bằng radian.
- Ví Dụ:
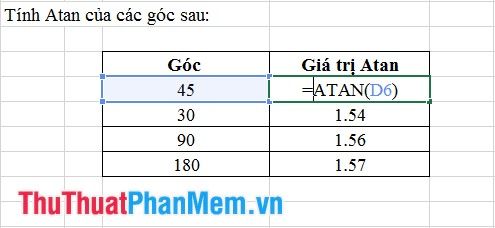
8. Hàm Atan
- Cú pháp: Atan (số).
Trong trường hợp này: số là giá trị cần tính Atan.
- Ý Nghĩa: Trả về giá trị Atan của một góc.
- Ví Dụ:
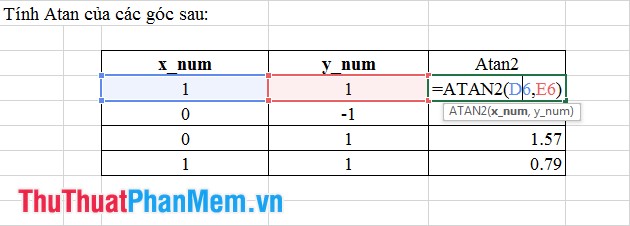
9. Hàm Góc ArcTangent 2
- Cú pháp: atan2(x, y).
Trong công thức trên, x và y là giá trị của hoành độ và tung độ tương ứng.
Ý nghĩa: Trả về giá trị góc radian nằm trong khoảng từ -π đến +π.
- Ví dụ: Chúng ta hãy xem một ví dụ về hàm Atanh.
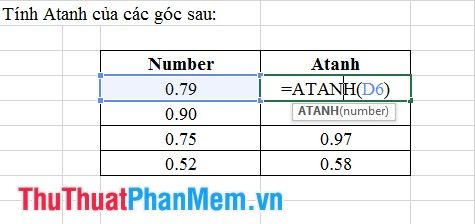
10. Hàm Tangent Hyperbolic Nghịch Đảo
- Cú pháp: atanh(số).
Ở đây, số là giá trị cần tính hàm Atanh.
- Ý nghĩa: Trả về giá trị trong đơn vị Radian.
- Ví dụ: Hãy xem một ví dụ về cách sử dụng hàm Degrees.
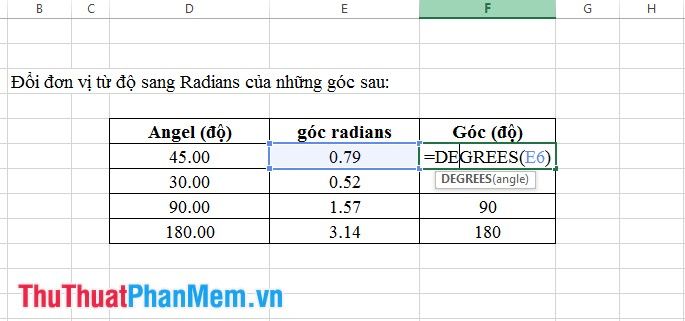
11. Hàm Chuyển Đổi Độ Sang Radian
- Cú pháp: degrees(góc).
Trong trường hợp này, angle là giá trị độ của một góc cần được chuyển đổi.
- Ý nghĩa: Chuyển đổi độ đo của một góc từ radians sang độ.
- Ví dụ: Hãy xem một ví dụ về cách sử dụng hàm Radians.
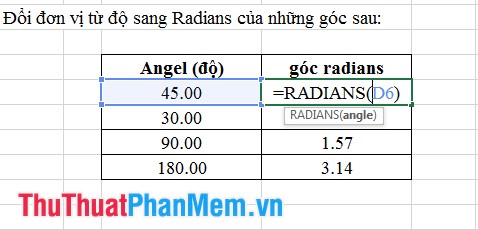
12. Hàm Chuyển Đổi Radian
- Cú pháp: radians(góc).
Trong trường hợp này, góc là giá trị độ của một góc cần chuyển đổi.
- Ý nghĩa: Chuyển đổi số đo của một góc từ đơn vị độ sang radians.
- Ví dụ: Hãy xem một ví dụ về cách sử dụng hàm Radians.
Chúc mọi người đạt được thành công lớn lao!
