Công thức chính xác để tính chu vi và diện tích hình tròn

1. Phân biệt đường tròn và hình tròn

Có nhiều người vẫn nhầm lẫn giữa đường tròn và hình tròn, nhưng trong hình học, chúng là hai khái niệm khác nhau. Cụ thể:

- Hình tròn bao gồm tất cả các điểm nằm bên trong và trên đường tròn, tức là tất cả các điểm cách tâm một khoảng không vượt quá bán kính. Ngược lại, đường tròn là tập hợp các điểm nằm trên mặt phẳng và cách đều một điểm cố định (tâm đường tròn) với khoảng cách bằng bán kính.

- Đường tròn không có diện tích như hình tròn

Đường tròn với tâm O và bán kính R bao gồm tất cả các điểm nằm cách tâm O một khoảng cách đúng bằng bán kính R. Những điểm này nằm trên đường tròn và khoảng cách từ tâm O đến các điểm trên đường tròn được gọi là bán kính.

1.1. Có ba vị trí khác nhau của một điểm đối với đường tròn

- Nếu điểm A nằm bên trong đường tròn có tâm O và bán kính R, thì khoảng cách OA sẽ nhỏ hơn R

- Nếu điểm A nằm trên đường tròn có tâm O và bán kính R, thì khoảng cách OA sẽ bằng R

- Nếu điểm A nằm ngoài đường tròn có tâm O và bán kính R, thì khoảng cách OA sẽ lớn hơn R

1.2. Các đặc điểm của đường tròn

- Các đường tròn có kích thước giống nhau sẽ có chu vi giống nhau

- Bán kính của mọi đường tròn bằng nhau luôn có kích thước đồng nhất

- Đường kính là đoạn thẳng dài nhất có thể vẽ trong hình tròn

- Góc tại tâm của một đường tròn luôn là 360 độ

- Chu vi của mỗi đường tròn khác nhau và tỷ lệ thuận với chiều dài của bán kính

- Các đoạn tiếp tuyến từ một điểm ngoài đường tròn vẽ cùng một đường tròn có chiều dài bằng nhau

1.3. Những đặc điểm của hình tròn

- Đường kính là một loại dây cung đặc biệt của hình tròn, đi qua tâm và là đoạn thẳng dài nhất cắt qua hình tròn, chia nó thành hai phần bằng nhau

- Độ dài của đường kính trong hình tròn gấp đôi bán kính của nó. Bán kính là khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn

2. Công thức tính chu vi của hình tròn

Chu vi của hình tròn là độ dài của đường bao quanh hình tròn. Để tính chu vi, bạn có thể sử dụng công thức dưới đây:

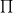
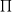
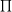
C = d x 3,14 = 2 x r x 3,14

3. Công thức tính diện tích của hình tròn

Để tính diện tích của hình tròn, bạn sử dụng công thức dưới đây:

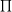
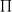
4. Các bài tập ứng dụng công thức tính chu vi và diện tích hình tròn

4.1. Ví dụ bài tập

Bài tập 1: Trên sân trường hình thang với trung bình cộng của hai đáy là 40 m và chiều cao 30 m, có một bồn hoa hình tròn được xây dựng với chu vi 12,56 m. Hãy tính diện tích còn lại của sân trường sau khi trừ diện tích bồn hoa.

Giải pháp:

Diện tích của sân trường là: 40 x 30 = 1200 (m²)

Diện tích còn lại của sân trường là: 1200 - 123,9 = 1076,1 (m²)

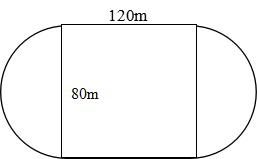
Bài tập 2: Một sân vận động có hình dạng và kích thước như minh họa dưới đây. Tính các giá trị sau:

a) Chu vi của sân vận động

b) Diện tích của sân vận động

Giải pháp:

Sân vận động bao gồm một hình chữ nhật với chiều dài 120m và chiều rộng 80m, cùng với hai nửa hình tròn có đường kính 80m.

Bài tập 3: Tính diện tích của hình tròn trong hình dưới, biết rằng hình vuông ABCD có đường chéo BD = 24 cm.

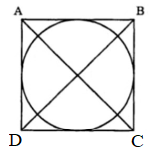
Giải pháp:

Gọi cạnh của hình vuông ABCD là a. Ta có: a^2 + a^2 = 24^2 => a^2 = 288 => a = 16,97 cm

Bán kính của hình tròn bằng một nửa cạnh của hình vuông ABCD => r = a/2 = 8,485 cm

Bài tập 4: Một tấm bảng chỉ đường hình tròn có đường kính 50 cm.

a) Diện tích của tấm bảng chỉ đường là bao nhiêu mét vuông?

b) Để sơn cả hai mặt của tấm bảng, mỗi mét vuông tiêu tốn 7000 đồng. Tính tổng chi phí sơn tấm bảng.

Giải pháp:

a) Bán kính của tấm bảng là: 50 / 2 = 25 (cm)

25 cm tương đương với 0,25 m

b) Để sơn tấm bảng đó, tổng chi phí là: 0,196 x 7000 = 1372 đồng

Bài tập 5: Miệng giếng nước có dạng hình tròn với bán kính 0,7 m. Thành giếng được xây rộng 0,3 m xung quanh miệng giếng. Tính diện tích của phần thành giếng.

Lời giải:

Diện tích của hình tròn nhỏ (miệng giếng) tính được là: 0,7 x 0,7 x 3,14 = 1,5386 (m²)

Bán kính của hình tròn lớn được tính là: 0,7 + 0,3 = 1 (m)

Diện tích của hình tròn lớn là: 1 x 1 x 3,14 = 3,14 (m²)

Diện tích của phần thành giếng được tính bằng: 3,14 - 1,5386 = 1,6014 (m²)

4.2. Một số bài tập tự luyện

Bài tập 1: Tính chu vi và diện tích của hình tròn với các bán kính sau:

a) r = 5 cm; r = 0,8 cm; r = 4/5 dm

b) d = 5,2 m; d = 1,2 m; d = 3/5 dm

Bài tập 2: Một cái nong hình tròn có chu vi là 376,8 cm. Tính diện tích của cái nong đó tính theo mét vuông?

Bài tập 3: Sân trường của bạn Hoa có dạng hình chữ nhật với chiều dài 45 m và chiều dài vượt chiều rộng 6,5 m. Giữa sân có một bồn hoa hình tròn đường kính 3,2 m. Tính diện tích còn lại của sân trường?

Bài tập 4: Trong sân trường, có hai bồn hoa hình tròn được trồng. Bồn hoa cúc có đường kính 40 dm, còn bồn hoa hồng có chu vi 9,42 m. Hãy so sánh diện tích của hai bồn hoa và tính sự chênh lệch diện tích giữa chúng.

Bài tập 5: 

a) Mặt bàn ăn hình tròn có chu vi 4,082 m. Tính bán kính của mặt bàn.

b) Biển báo giao thông có dạng hình tròn và chu vi 1,57 m. Xác định đường kính của biển báo.

Bài tập 6: Một bánh xe ô tô có bán kính 0,25 m. Tính các thông số liên quan.

a) Đường kính của bánh xe là bao nhiêu mét?

b) Chu vi của bánh xe là bao nhiêu mét?

Bài tập 7: Một hình tròn có chu vi 254,24 dm. Xác định đường kính và bán kính của hình tròn đó.

Bài tập 8: Một hình tròn có bán kính bằng cạnh của một hình vuông có chu vi 25 cm. Tính chu vi của hình tròn.

Bài tập 9: Hình tròn có tâm O và đường kính AB = 8 cm. Xác định các thông số liên quan.

a) Tính chu vi của các hình tròn với tâm O và đường kính AB, tâm M và đường kính OA, và tâm N và đường kính OB.

b) So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi của hình tròn tâm O.

Bài tập 10: Xác định bán kính của hình tròn với chu vi C = 16,328 dm và C = 8,792 cm.

Trên đây là hướng dẫn của Mytour về công thức tính chu vi và diện tích hình tròn chính xác. Hy vọng thông tin này sẽ hỗ trợ các bạn học sinh trong việc giải các bài tập liên quan đến chu vi và diện tích hình tròn.