1. Hình tam giác là gì?
Hình tam giác là một hình học cơ bản trong hệ thống hình học phẳng, là một đa giác lồi với tổng các góc nhỏ hơn 180°. Hình tam giác có ba đỉnh, nối với nhau bằng ba cạnh, không nằm trên một đường thẳng.
2. Các công thức tính diện tích hình tam giác
Đơn vị đo diện tích của tam giác có thể là: cm², m², dm², v.v.
2.1 Công thức tính diện tích cho tam giác thông thường
Tam giác thông thường có các đặc điểm sau:
- Độ dài ba cạnh của tam giác không bằng nhau;
- Các góc trong tam giác có số đo khác nhau.
* Công thức tính diện tích tam giác cơ bản
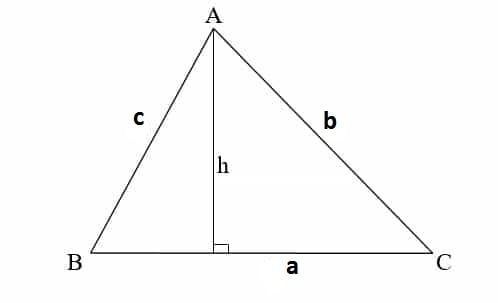
Để tính diện tích của tam giác, bạn lấy chiều cao nhân với độ dài của cạnh đáy rồi chia đôi. Công thức cụ thể như sau:
.png)
Chú thích:
- h: là chiều cao của tam giác, tức là đoạn thẳng từ đỉnh của tam giác vuông góc với cạnh đáy đối diện. Chiều cao phải được hạ đúng góc vuông xuống đáy.
- a = BC: chính là cạnh đáy của tam giác.
Ví dụ: Giả sử có tam giác ABC (như trong hình), với chiều cao là h = 8cm và cạnh đáy BC = 20cm. Tính diện tích của tam giác ABC?
Giải
Diện tích của tam giác ABC được tính như sau:
SABC = ( a x h ) / 2 = ( BC x h ) / 2 = ( 20 x 8 ) / 2 = 80 cm²
2.2 Công thức tính diện tích của tam giác cân
Tam giác cân có những đặc điểm sau:
- Hai cạnh bên của tam giác này có chiều dài bằng nhau;
- Hai góc đáy của tam giác cân có số đo góc bằng nhau;
* Công thức tính diện tích của tam giác cân
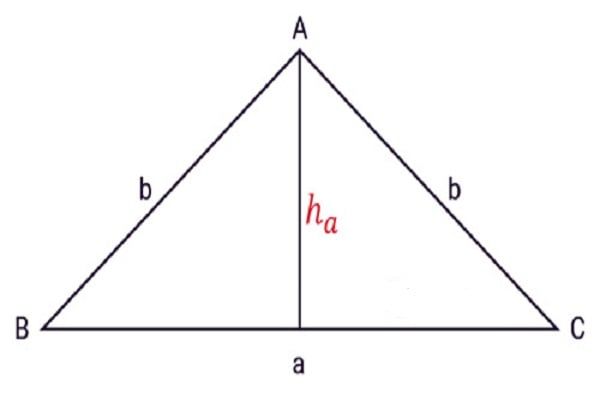
Tương tự như diện tích của tam giác thường, diện tích tam giác cân được tính bằng một nửa tích của chiều cao (đoạn thẳng từ đỉnh xuống cạnh đáy, phải vuông góc với đáy). Công thức cụ thể như sau:
(1).png)
Quy định:
- h: được định nghĩa là chiều cao của tam giác;
- a = BC: được định nghĩa là chiều dài của cạnh đáy tam giác.
Ví dụ: Xét tam giác cân ABC (như hình vẽ) với các thông số như sau: Hai cạnh bên AB = AC = b = 8cm; cạnh đáy BC = a = 14cm và chiều cao từ đỉnh A đến cạnh đáy BC là h = 10cm. Tính diện tích của tam giác ABC?
Giải pháp
Diện tích của tam giác cân ABC được tính như sau:
SABC = ( a x h ) / 2 = ( BC x h ) / 2 = ( 14 x 10 ) / 2 = 70 cm²
2.3 Công thức tính diện tích của tam giác vuông
Tam giác vuông có các đặc điểm sau đây:
- Tam giác này có một góc vuông (90°).
- Trong tam giác vuông, cách xác định các cạnh như sau:
+ Cạnh đối diện góc vuông (90°) được gọi là cạnh huyền, đây là cạnh dài nhất trong tam giác vuông;
+ Hai cạnh còn lại của tam giác gọi là các cạnh góc vuông.
- Đối với bài tập tam giác vuông, định lý Pythagoras rất phổ biến, thường được sử dụng để giải các bài toán về tam giác vuông, bao gồm tính diện tích.
* Công thức tính diện tích của tam giác vuông
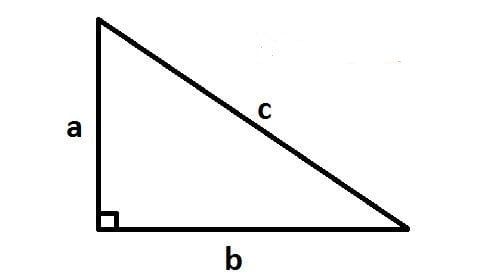
Tam giác vuông khác biệt với tam giác thường ở chỗ chiều cao của nó trùng với một cạnh góc vuông, và cạnh góc vuông còn lại là cạnh đáy. Do đó, diện tích tam giác vuông được tính bằng một nửa tích của hai cạnh góc vuông (1/2 chiều cao nhân với cạnh đáy). Công thức cụ thể như sau:
.png)
Quy định:
- a: là chiều cao của tam giác vuông (tương ứng với chiều dài của một cạnh góc vuông)
- b: là một trong các cạnh góc vuông của tam giác.
Ví dụ: Xét tam giác vuông (như hình vẽ) với các cạnh góc vuông có chiều dài a = 5cm và b = 15cm. Tính diện tích của tam giác vuông này?
Giải pháp
Diện tích của tam giác vuông được tính như sau:
S = ( a x b ) / 2 = ( 5 x 15 ) / 2 = 37,5 cm²
2.4 Công thức tính diện tích tam giác đều
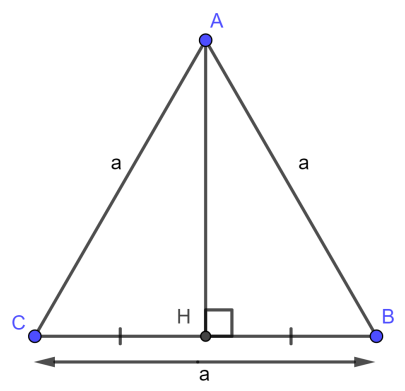
Tam giác đều có những đặc điểm giống như các loại tam giác khác, nhưng cũng có những điểm khác biệt đặc trưng như sau:
- Ba cạnh của tam giác đều có chiều dài như nhau;
- Ba góc của tam giác đều có số đo bằng nhau và đều là 60°
* Công thức tính diện tích của tam giác đều
Tương tự như tam giác thường, diện tích của tam giác đều được tính bằng một nửa tích của chiều cao và chiều dài cạnh đáy. Công thức cụ thể như sau:
(2).png)
Quy định:
- S: là diện tích của tam giác;
- a: là chiều dài của cạnh đáy tam giác;
- h: là chiều cao của tam giác đều.
Ví dụ: Xét tam giác đều ABC (như hình vẽ trên) với chiều dài các cạnh: AB = BC = AC = a = 12cm; và chiều cao AH = h = 8cm. Tính diện tích của tam giác ABC.
Giải pháp
Diện tích của tam giác ABC được tính như sau:
SABC = ( AH x BC ) / 2 = ( a x h ) / 2 = ( 12 x 8 ) / 2 = 48 cm²
Trên đây là những công thức cơ bản để tính diện tích tam giác. Tùy thuộc vào từng dạng bài tập, các công thức này có thể được điều chỉnh theo chương trình học của mỗi học sinh.
Bài viết này nhằm mục đích giáo dục và không vì mục đích thương mại. Hy vọng thông tin cung cấp hữu ích cho bạn. Cảm ơn và trân trọng kính chào!
