Công thức chuẩn nhất để tính diện tích và chu vi hình thoi

1. Định nghĩa hình thoi

Hình thoi là tứ giác có bốn cạnh bằng nhau, hoặc là một hình bình hành với hai đường chéo vuông góc và cắt nhau tại trung điểm, cũng là đường phân giác của các góc.

Khi hình thoi có bốn góc vuông bằng nhau, nó trở thành hình vuông. Do đó, hình vuông là một dạng đặc biệt của hình thoi với bốn cạnh bằng nhau và bốn góc vuông.

Mọi hình vuông đều là hình thoi, nhưng không phải hình thoi nào cũng là hình vuông.

2. Các tính chất của hình thoi

Trước hết, hình thoi có đầy đủ các tính chất của hình bình hành: các cạnh đối song song và bằng nhau, các góc đối bằng nhau, và hai đường chéo cắt nhau tại trung điểm mỗi đường.

Ngoài ra, hình thoi có các góc đối bằng nhau và tổng các góc trong hình là 360 độ.

Thứ ba, hình thoi có hai đường chéo vuông góc và giao nhau tại trung điểm của mỗi đường.

Thứ tư, các đường chéo của hình thoi cũng đồng thời là các đường phân giác của các góc trong hình.

3. Cách nhận diện hình thoi

Dấu hiệu 1: Hình thoi là một tứ giác có bốn cạnh bằng nhau.

Dấu hiệu 2: Hình thoi có hai đường chéo vuông góc và cắt nhau tại trung điểm của mỗi đường.

Dấu hiệu 3: Hình thoi là một loại hình bình hành với hai cạnh kề nhau có độ dài bằng nhau.

Dấu hiệu 4: Hình thoi là hình bình hành mà hai đường chéo của nó vuông góc với nhau.

Dấu hiệu 5: Hình thoi là hình bình hành có đường chéo đóng vai trò là phân giác của một góc trong hình.

4. Cách tính chu vi của hình thoi

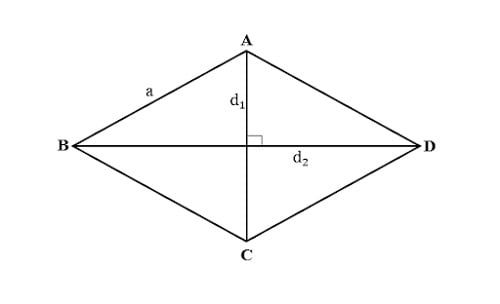
Để tính chu vi của hình thoi, bạn cần cộng tất cả các cạnh lại với nhau hoặc nhân độ dài một cạnh với 4. Dưới đây là công thức tính chu vi hình thoi:

P = a + a + a + a = a x 4

Trong đó: P là chu vi của hình thoi, a là độ dài của một cạnh hình thoi

Ví dụ: Cho một hình thoi ABCD với các cạnh đều dài 4 cm. Vậy chu vi của hình thoi là bao nhiêu?

Áp dụng công thức tính chu vi hình thoi với cạnh a = 4 cm.

Giải:

Chu vi của hình thoi ABCD được tính như sau:

4 x 4 = 16 (cm)

Kết quả: 16 (cm)

5. Công thức tính diện tích hình thoi

Diện tích của hình thoi được tính bằng nửa tích của độ dài hai đường chéo. Đường chéo trong hình thoi là các đoạn thẳng nối các đỉnh đối diện, và chúng cắt nhau vuông góc tại trung điểm của mỗi đường. Công thức tính diện tích hình thoi như sau:

S = 1/2 x (d1 x d2)

Trong đó: S đại diện cho diện tích hình thoi, d1 và d2 là các đường chéo của hình thoi

Ví dụ: Cho hình thoi ABCD với độ dài hai đường chéo lần lượt là 6 cm và 10 cm. Hãy tính diện tích của hình thoi ABCD.

Giải pháp:

Diện tích của hình thoi ABCD được tính như sau:

6 x 10 / 2 = 30 (cm²)

Kết quả: 30 (cm²)

Bên cạnh công thức trên, còn có một số phương pháp khác để tính diện tích hình thoi, chẳng hạn như:

Đầu tiên, chúng ta có thể tính diện tích hình thoi dựa vào các công thức trong tam giác, đặc biệt khi biết số đo các góc của hình thoi.

S = a² . sin A = a² . sin B = a² . sin C = a² . sin D

Ví dụ: Xét hình thoi ABCD với mỗi cạnh dài 4 cm và góc A có số đo 30°. Tính diện tích của hình thoi ABCD.

Giải pháp:

* Phương pháp 1:

Diện tích của hình thoi ABCD được tính như sau:

S = a² . sin A = 4² . sin30° = 16 . 1/2 = 8 (cm²)

Do đó, diện tích của hình thoi ABCD là 8 cm².

* Phương pháp 2:

Vì ABCD là hình thoi, các tam giác bên trong đều là tam giác cân.

Gọi O là giao điểm của hai đường chéo AC và BD, nơi O cũng là trung điểm của các đường chéo này, nên AO vuông góc với BD. Từ đó, góc BAO = 1/2 góc BAD = 15°.

Do đó: AO = AB . cos BAO = 4 . cos15° = 3,84 (cm)

Sử dụng định lý Pythagoras cho tam giác AOB, ta có:

AB² = AO² + OB² ⇔ OB² = AB² - AO² = 4² - 3,84² = 1,25

⇒ OB = 1,1 (cm)

Kết quả tính toán: AC = 2 x AO = 2 x 3,84 = 7,68 cm và BD = 2 x OB = 2 x 1,1 = 2,2 cm

Diện tích hình thoi ABCD được tính bằng công thức: S = 1/2 x AC x BD = 1/2 x 7,68 x 2,2 = 8,45 cm²

Do đó, diện tích của hình thoi ABCD là 8,45 cm²

Thứ hai, có một công thức khác để tính diện tích hình thoi dựa vào cạnh đáy và chiều cao.

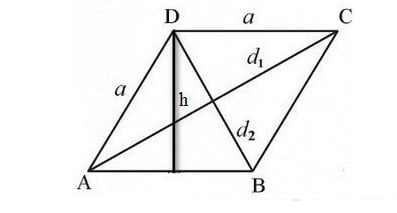
S = h x a

Ở đây, S đại diện cho diện tích của hình thoi, h là chiều cao và a là chiều dài cạnh đáy

Ví dụ: Xét hình thoi ABCD với các cạnh AB = BC = CD = DA = 5 cm và chiều cao bằng 4 cm. Tính diện tích của hình thoi này.

Giải:

Áp dụng công thức tính diện tích, với h = 4 cm và a = 5 cm, ta có:

S = a x h = 5 x 4 = 20 (cm²)

Do đó, diện tích của hình thoi ABCD là 20 (cm²)

6. Một số ví dụ áp dụng công thức tính chu vi và diện tích của hình thoi

Ví dụ 1: Một mảnh đất hình thoi có tổng độ dài hai đường chéo là 400 cm. Độ dài đường chéo thứ nhất bằng 3/5 độ dài đường chéo thứ hai. Tính diện tích của mảnh đất hình thoi này?

Giải:

Tổng số phần bằng nhau là: 3 + 5 = 8 (phần)

Chiều dài của đường chéo thứ hai là: 400 : 8 x 5 = 250 (cm)

Chiều dài của đường chéo thứ nhất là: 400 - 250 = 150 (cm)

Diện tích hình thoi được tính là: 250 x 150 : 2 = 18750 (cm²)

Kết quả: 18750 (cm²)

Ví dụ 2: Một khu đất hình thoi có chiều dài đường chéo đầu tiên là 20 m. Đường chéo thứ hai dài bằng 3/4 chiều dài đường chéo đầu tiên. Nếu bác nông dân trồng khoai tây trên khu đất này và thu hoạch được 5 kg mỗi mét vuông, hãy tính tổng lượng khoai tây thu hoạch được.

Giải:

Chiều dài của đường chéo thứ hai là: 20 : 4 x 3 = 15 (m)

Diện tích khu đất hình thoi là: 20 x 15 : 2 = 150 (m²)

Tổng lượng khoai tây thu hoạch được là: 150 x 5 = 750 (kg)

Kết quả: 750 kg khoai tây

Ví dụ 3: Trong hình thoi ABCD, O là điểm giao nhau của hai đường chéo. Biết rằng diện tích hình thoi là 60 cm² và AC = 10 cm, hãy tính độ dài của cạnh hình thoi.

Giải:

Diện tích hình thoi được tính như sau:

S = 1/2 x AC x BD ⇒ BD = (2 x S) / AC = (2 x 60) / 10 = 12 (cm)

Theo đặc điểm của hình thoi, O là trung điểm của hai đường chéo AC và BD

Do đó: OA = 1/2 x AC = 1/2 x 10 = 5 (cm) và OB = 1/2 x BD = 1/2 x 12 = 6 (cm)

Áp dụng định lý Pythagoras trong tam giác AOB, ta tính được:

AB² = OA² + OB² = 5² + 6² = 61, từ đó AB = 7,81 (cm)

Do đó, độ dài của cạnh hình thoi là: 7,81 cm