1. Cách tính thể tích khối lăng trụ
Để tính thể tích của khối lăng trụ đứng, áp dụng công thức: V = S.h
Trong đó:
S đại diện cho diện tích của đáy; đáy của lăng trụ có thể là hình vuông, hình chữ nhật, hình tam giác, hoặc hình tròn. Bạn cần tính diện tích đáy dựa trên hình dạng cụ thể của lăng trụ.
h là chiều cao của khối lăng trụ, chính là khoảng cách từ đỉnh đến đáy của lăng trụ.
Lưu ý:
Đối với lăng trụ đều, đáy là một đa giác đều. Để tính thể tích V của lăng trụ đều, áp dụng công thức: V = 1/3 x S x h; trong đó S là diện tích đáy đều và h là chiều cao của lăng trụ đều.
Thể tích của khối lăng trụ chữ nhật được tính như sau: với lăng trụ hình chữ nhật, đáy là hình chữ nhật có chiều dài a và chiều rộng b. Để tính thể tích V của lăng trụ chữ nhật, sử dụng công thức: V = S x h; với S là diện tích đáy hình chữ nhật và h là chiều cao của lăng trụ chữ nhật.
Thể tích của một khối lập phương được tính dựa vào độ dài cạnh của nó. Nếu cạnh của khối lập phương là a, thì thể tích V có thể được tính bằng công thức V = a x a x a, với a là độ dài cạnh.
2. Bài tập về công thức tính thể tích của khối lăng trụ
Câu 1. Xét lăng trụ đứng ABC với đáy là tam giác vuông cân tại A, với AB = AC = a và AA’ = 2a. Tính thể tích của lăng trụ ABC. A’B’C’.
A. 2a3
B. 2a3
C. a3/3
D. a3
Câu 2. Một lăng trụ đứng có đáy là tam giác vuông cân tại A, với cạnh AB = a√ 3, góc giữa A'C và mặt (ABC) là 45°. Tính thể tích của lăng trụ này.
A. 3√ 3/2 . a3
B. a3
C. 3√ 3 a3
D. a3/2
Câu 3. Tính thể tích của khối lập phương có đường chéo dài √ 12.
A. 8
B. 24
C. 12
D. 16
Câu 4. Cho lăng trụ đứng ABC.A’B’C’ có thể tích là V. Trong số các khối chóp dưới đây, khối chóp nào có thể tích bằng 2V /3?
A. A.A'B'C'
B. C'.ABC
C. A'.BCC'B'
D. I.ABB'A'
Câu 5. Một hình hộp đứng có các cạnh AB = 3a, AD = 2a, và AA' = 2a. Tính thể tích của khối chóp A’.ACD’.
A. a3
B. 2a3
C. 3a3
D. 6a3
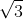
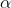
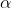 3
3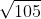 3
3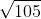 3
3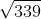 3
3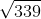
Câu 7. Đối với khối lập phương có đường chéo dài d, thể tích của khối lập phương là:
A. V = d3
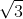 3
3C. 3d3
3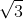
Câu 8. Một lăng trụ đứng ABC.A’B’C’ với đáy là tam giác cân, AB = AC = a và góc BAC = 120º. Mặt phẳng (AB'C') tạo với mặt đáy một góc 60º. Tính thể tích của lăng trụ ABC.A’B’C’.
A. 8/3 a3
B. 3/8 a3
C. a3/8
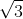 3
3Câu 9. Cho hình hộp chữ nhật ABCD.A’B’C’D’ với các cạnh AB = a, BC = b, và AA' = c. M và N lần lượt là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích của hình hộp chữ nhật ABCD.A’B’C’D’.
A. 1/2
B. 1/5
C. 1/8
D. 1/4
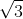
A. 6a3
B. 8a3
C. 4a3
D. 2a3
Câu 11. Một lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân tại A, với AB = AC = a và góc BAC = 120º. Hình chiếu của A’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC, cạnh bên AA' dài 2a. Tính thể tích của lăng trụ.
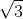
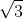
C. 3a3/4
3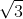
Câu 12: Xét hình hộp đứng ABCD A'B'C'D' với đáy ABCD là hình thoi cạnh a và góc BAD = 60°. Biết AB' tạo với mặt đáy (ABCD) một góc 30°. Tính thể tích của hình hộp.
A. 3a3
B. a3/4
C. 3a3/ 2
D. a3
Câu 13. Cho khối lăng trụ tam giác đều ABC.A’B’C’. Gọi M là trung điểm của cạnh AA’. Mặt phẳng (MBC) chia khối lăng trụ thành hai phần. Tỉ lệ thể tích của hai phần này là:
A. 1 /3
B. 1 /5
C. 1 /6
D. 3/ 5
Câu 14. Cho khối lăng trụ tứ giác đều ABCD.A’B’C’D’ với khoảng cách giữa hai đường thẳng AB và A’D là 2 và độ dài đường chéo của mặt bên là 5. Vẽ đường vuông góc AK từ A' đến A'D, với K nằm trên A'D. Khi đó, độ dài của AK là
A. 1
B. 2
C. 3
D. 4
3. Hướng dẫn cách giải bài tập về công thức tính thể tích khối lăng trụ
Câu 1.
.png)
Chọn D
Chiều cao của lăng trụ là AA’ = 2a.
Diện tích đáy là: SABC = 1/2 AB.AC = 1/2 . a . a = a2/2
Thể tích của khối lăng trụ là: V ABC.A'B'C' = S ABC . AA' = a2/2 . 2a = a3
Câu 2.
Chọn A.
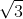
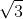
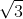
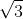 2
2Góc giữa AC' và mặt phẳng (ABC) là 45º => A'CA = 45º
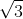
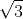 2
2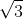
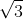 3
3Câu 3.
Chọn A.
Gọi AB = a. Vì đáy là hình vuông nên BD = a√2
Vì góc vuông tại B nên BD2 = BB’2 + BD2
12 = a2 + 2a2 ⇔ a = 2.
Do đó, thể tích của khối lập phương ABCD.A’B’C’D’ là: V ABCD.A'B'C'D' = a3 = 23 = 8.
Câu 4.
Có: V ABC.A'B'C' = V A'.BCC'B' + VA'.ABC.
Vì VA'.ABC = 1/3. V ABC.A'B'C' nên VA'.BCC'B' = 2/3. V ABC.A'B'C' = 2/3V.
Do đó, chọn đáp án C.
Câu 5.
.png)
Có: VA’.ACD’ = 1/2.V C.ADD' = 1/2 . 1/3. V ABCD.A'B'C'D' = 1/6. 3a. 2a. 2a = 2a3
Vậy chọn đáp án B
Câu 6.
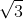 2
2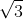
Kẻ CH vuông góc với AB => CH vuông góc với mặt phẳng ABB'A' nên B’H là hình chiếu vuông góc của B’C lên mặt phẳng ABB'A => (B'C, (ABB'A')) = (B'C, B'H) và CB'H
2222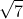
Xét tam giác BB'C vuông tại B, ta có: BB'² + B'C² = BC² = 7a². Do đó, thể tích của khối là: V = SABC . AA' = (3a² / 7) . 2a = 6a³ / 7 = 28
Chọn đáp án A
Câu 7.
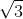
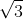 33
33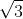
Do đó, chọn đáp án D.
Câu 8.
.png)
Xác định góc giữa mặt phẳng (AB'C') và mặt đáy là AKA' => AKA' = 60º
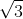
V ABC.A'B'C' = S ABC . AA' = 3/8.a3
Do đó, chọn đáp án B.
Câu 9.
Thể tích của khối chóp D’.DMN bằng thể tích của khối chóp D.D’MN
Có S D'MN = S A'B'C'D' - (S D'A'M + S D'C'N + S B'MN) = ab - (ab /4 + ab /4 + ab /8) = 3ab /8
Thể tích khối chóp D’.DMN là: V1 = 1/3 S D'MN . DD' = 1/3 . 3ab/8 . c = abc /8
Thể tích của khối hộp chữ nhật ABCD.A’B’C’D’ là V = abc => V1 / V = 1/8
Do đó, chọn đáp án C.
Câu 10.
.png)
Gọi M là trung điểm của cạnh BC, G là trọng tâm của tam giác ABC
Ta có GA vuông góc với mặt phẳng (ABC) => GA = (ABC) hc A A' => (A A', (ABC)) = A' AG = 30º
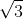
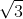 2
2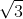 2
2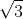
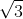
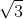
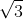
Vậy thể tích của khối lăng trụ ABC.A'B'C' là: V ABC.A'B'C' = S ABC . A'A = 6a3
Do đó, chọn đáp án A.
