Công thức để tính Tích có hướng của hai vecto trong không gian rất thú vị và chi tiết.

Buzz

Nội dung bài viết

1. Công thức tính tích có hướng của hai vecto trong không gian

2. Giáo trình về tích vô hướng của hai vectơ trong không gian

3. Bài tập ứng dụng tích có hướng của hai vectơ trong không gian

Xem thêm

Bài viết này từ Mytour sẽ cung cấp thông tin chi tiết về công thức tính Tích có hướng của hai vecto trong không gian. Hy vọng thông tin sẽ hữu ích cho bạn!

1. Công thức tính tích có hướng của hai vecto trong không gian

Tích có hướng là phép toán nhị phân trên các vecto trong không gian ba chiều, khác với nhân vô hướng vì kết quả là một vecto giả thay vì một số vô hướng.

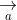
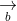
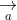
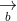
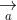
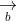
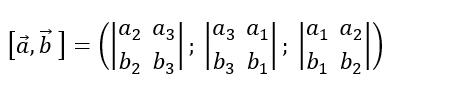
$\underset{a}{\rightarrow}$ $\underset{b}{\rightarrow}$ $\underset{a}{\rightarrow}$ $\underset{b}{\rightarrow}$ $\underset{a}{\rightarrow}$ $\underset{b}{\rightarrow}$ Công thức để tính Tích có hướng của hai vecto trong không gian rất chi tiết và hấp dẫn.

Công thức để tính Tích có hướng của hai vecto trong không gian rất chi tiết và hấp dẫn.

= (a2b3 - a3b2; a3b1 - a1b3; a1b2 - a2b1)

Lưu ý: Tích có hướng của hai vecto tạo ra một vecto, trong khi tích vô hướng của hai vecto là một số.

Đặc điểm

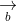
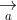
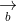
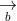
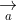
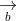
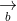
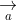
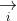
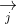
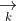
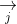
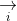
$\underset{a}{\rightarrow}$ $\underset{b}{\rightarrow}$ $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$ $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$ $\underset{a}{\rightarrow}$ $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$ $\underset{a}{\rightarrow}$ $\underset{i}{\rightarrow}$ $\underset{j}{\rightarrow}$ $\underset{k}{\rightarrow}$ $\underset{j}{\rightarrow}$ $\underset{i}{\rightarrow}$ $\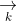underset{k}{\rightarrow}$ $\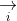underset{i}{\rightarrow}$ $\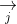underset{j}{\rightarrow}$ $\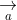underset{a}{\rightarrow}$ $\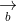underset{b}{\rightarrow}$ $\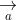underset{a}{\rightarrow}$ $\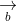underset{b}{\rightarrow}$ $\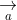underset{a}{\rightarrow}$ $\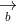underset{b}{\rightarrow}$ $\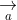underset{a}{\rightarrow}$ $\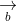underset{b}{\rightarrow}$ $\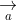underset{a}{\rightarrow}$ $\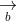underset{b}{\rightarrow}$

Các ứng dụng của tích có hướng (chương trình nâng cao)

+ Điều kiện để ba vecto đồng phẳng:

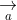
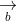
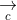
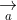
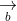
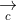
$\underset{a}{\rightarrow}$ $\underset{b}{\rightarrow}$ $\underset{c}{\rightarrow}$ $\underset{a}{\rightarrow}$ $\underset{b}{\rightarrow}$ $\underset{c}{\rightarrow}$

+ Diện tích hình bình hành ABCD:

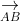
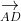
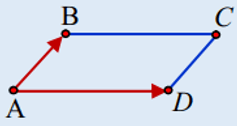
$\underset{AB}{\rightarrow}$ $\underset{AD}{\rightarrow}$ Công thức tính Tích có hướng của hai vecto trong không gian rất chi tiết và hấp dẫn.

+ Diện tích tam giác ABC:

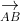
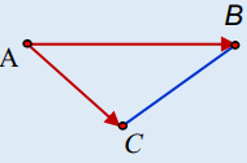
$\underset{AB}{\rightarrow}$ $\underset{AC}{\rightarrow}$ Công thức tính Tích có hướng của hai vecto trong không gian rất chi tiết và dễ hiểu.

+ Thể tích của khối hộp ABCD.A’B’C’D’:

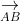
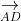
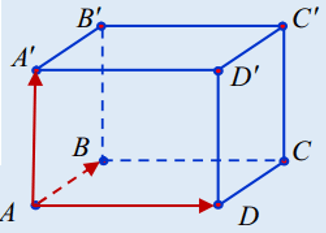
$\underset{AB}{\rightarrow}$ $\underset{AD}{\rightarrow}$ $\underset{AA'}{\rightarrow}$ Công thức chi tiết về Tích có hướng của hai vecto trong không gian.

+ Thể tích của tứ diện ABCD

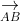
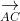
$\underset{AB}{\rightarrow}$ $\underset{AC}{\rightarrow}$ $\underset{AD}{\rightarrow}$ Công thức chi tiết về Tích có hướng của hai vecto trong không gian.

Ví dụ thực tế

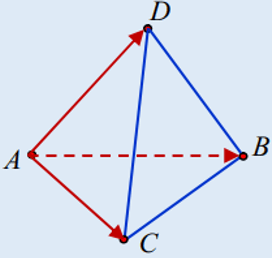
Bài 1: Trong không gian với hệ tọa độ Oxyz, cho 4 điểm A(1; 0; 1), B(-1; 1; 2), C(-1; 1; 0), D(2; -1; -2).

a) Chứng minh rằng các điểm A, B, C, D là 4 đỉnh của một tứ diện.

b) Tính thể tích của tứ diện ABCD và từ đó xác định độ dài của đường cao từ đỉnh A.

Giải quyết:

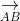
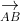
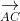
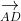
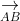
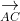
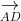
$\underset{AB}{\rightarrow}$ $\underset{AC}{\rightarrow}$ $\underset{AD}{\rightarrow}$ $\underset{AB}{\rightarrow}$ $\underset{AC}{\rightarrow}$ $\underset{AB}{\rightarrow}$ $\underset{AC}{\rightarrow}$ $\underset{AD}{\rightarrow}$ $\underset{AB}{\rightarrow}$ $\underset{AC}{\rightarrow}$ $\underset{AD}{\rightarrow}$

Do đó, A, B, C, D chính là 4 đỉnh của một tứ diện.

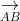
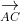
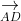
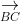
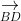
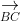
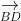
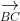
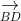
$\underset{AB}{\rightarrow}$ $\underset{AC}{\rightarrow}$ $\underset{AD}{\rightarrow}$ $\underset{BC}{\rightarrow}$ $\underset{BD}{\rightarrow}$ $\underset{BC}{\rightarrow}$ $\underset{BD}{\rightarrow}$ $\underset{BC}{\rightarrow}$ $\underset{BD}{\rightarrow}$

Thể tích tứ diện ABCD bằng 1/3 d(A;(BCD)).SBCD

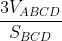
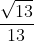
$\frac{3V_{ABCD}}{S_{BCD}}$ $\frac{\sqrt{13}}{13}$

Bài 2: Trong không gian với hệ tọa độ Oxyz, có 4 điểm A(-3; 5; 15), B(0; 0; 7), C(2; -1; 4), D(4; -3; 0). Chứng minh rằng AB và CD cắt nhau.

Giải pháp:

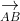
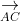
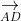
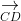
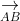
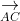
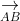
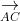
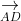
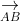
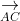
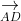
$\underset{AB}{\rightarrow}$ $\underset{AC}{\rightarrow}$ $\underset{AD}{\rightarrow}$ $\underset{CD}{\rightarrow}$ $\underset{AB}{\rightarrow}$ $\underset{AC}{\rightarrow}$ $\underset{AB}{\rightarrow}$ $\underset{AC}{\rightarrow}$ $\underset{AD}{\rightarrow}$ $\underset{AB}{\rightarrow}$ $\underset{AC}{\rightarrow}$ $\underset{AD}{\rightarrow}$

⇒ A, B, C, D nằm trong cùng một mặt phẳng (1)

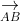
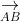
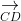
$\underset{AB}{\rightarrow}$ $\underset{AB}{\rightarrow}$ $\underset{CD}{\rightarrow}$

Dựa vào (1) và (2) cho thấy AB và CD giao nhau.

Bài 3: Trong không gian với hệ trục tọa độ Oxyz, có hình hộp ABCD.EFGH với các điểm A(1; 1; 1), B(2; 1; 2), E(-1; 2; -2), D(3; 1; 2). Tính khoảng cách từ điểm A đến mặt phẳng (DCGH).

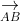
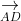
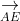
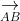
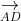
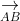
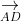
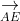
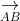
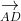
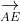
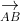
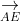
$\underset{AB}{\rightarrow}$ $\underset{AD}{\rightarrow}$ $\underset{AE}{\rightarrow}$ $\underset{AB}{\rightarrow}$ $\underset{AD}{\rightarrow}$ $\underset{AB}{\rightarrow}$ $\underset{AD}{\rightarrow}$ $\underset{AE}{\rightarrow}$ $\underset{AB}{\rightarrow}$ $\underset{AD}{\rightarrow}$ $\underset{AE}{\rightarrow}$ $\underset{AB}{\rightarrow}$ $\underset{AE}{\rightarrow}$

⇒ S_{DCGH} = S_{AEFB} = √3

V_{ABCD.EFGH} = d(A; (DCGH)) cdot S_{DCGH}

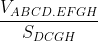
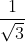
$\frac{V_{ABCD.EFGH}}{S_{DCGH}}$ $\frac{1}{\sqrt{3}}$

2. Giáo trình về tích vô hướng của hai vectơ trong không gian

I. MỤC TIÊU:

1. Kiến thức và kỹ năng: Sau khi hoàn thành bài học, học sinh sẽ đạt được các mục tiêu sau:

Hiểu và xác định góc giữa hai vectơ, thực hiện phép tích vô hướng của chúng.

Áp dụng tích vô hướng vào các bài toán hình học cụ thể.

Nhận thức mối liên hệ giữa tích vô hướng và khái niệm công trong vật lý.

2. Năng lực

- Năng lực chung:

Khả năng tự học và khám phá độc lập.

Kỹ năng giao tiếp và hợp tác trong việc trình bày, thảo luận, và làm việc nhóm.

Khả năng giải quyết vấn đề và sáng tạo trong thực hành và ứng dụng.

Năng lực cá nhân:

Khả năng tư duy và lập luận toán học.

Kỹ năng mô hình hóa toán học và giải quyết các bài toán toán học, ví dụ, ứng dụng giải thích công sinh bởi các lực không đổi cùng tác động lên một vật chuyển động thẳng và so sánh với công sinh bởi lực tổng hợp.

Khả năng giao tiếp trong toán học.

Sử dụng các công cụ và phương tiện học toán.

Thực hiện các phép toán theo đúng thứ tự, tính toán chính xác

3. Phẩm chất cá nhân

Có tinh thần học tập tích cực, khát khao khám phá và sáng tạo, đồng thời biết làm việc nhóm và tôn trọng ý kiến của các thành viên khác.

Chăm chỉ và tích cực trong việc xây dựng bài, có trách nhiệm và chủ động tiếp thu kiến thức theo sự hướng dẫn của giáo viên.

II. CÔNG CỤ VÀ TÀI LIỆU DẠY HỌC

Đối với giáo viên: Sách giáo khoa, tài liệu giảng dạy, giáo án, công cụ dạy học, thước kẻ có chia vạch, phiếu học tập.

Đối với học sinh: Sách giáo khoa, sách bài tập, vở ghi, giấy nháp, dụng cụ học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.

III. QUY TRÌNH DẠY HỌC

TIẾT 1: GÓC VÀ TÍCH VÔ HƯỚNG CỦA HAI VECTƠ

HOẠT ĐỘNG KHỞI ĐẦU (MỞ ĐẦU)

a) Mục tiêu:

- Nêu vấn đề về việc hình thành khái niệm toán học tích vô hướng và áp dụng định nghĩa công sinh bởi lực trong vật lý.

b) Nội dung: Học sinh chú ý lắng nghe và ghi nhớ.

c) Sản phẩm: Học sinh sẽ có cái nhìn ban đầu về bài học, đặc biệt là về tích vô hướng của hai vectơ.

d) Cách tổ chức thực hiện:

Bước 1: Giao nhiệm vụ:

- Giáo viên hướng dẫn:

Trong vật lý, nếu một lực không đổi tác động lên một vật tại điểm O và làm vật đó di chuyển một đoạn đường s = OM, công A của lực được tính theo công thức với F là cường độ lực (đơn vị Newton, N), s là độ dài của vectơ (đơn vị mét, m), và θ là góc giữa hai vectơ, công A được tính bằng Jun (J).

Trong toán học, giá trị của biểu thức này (không tính đơn vị đo) được gọi là gì?

Bước 2: Thực hiện nhiệm vụ: Học sinh quan sát, lắng nghe và đưa ra dự đoán cho câu hỏi.

Bước 3: Báo cáo và thảo luận: Giáo viên yêu cầu một số học sinh trình bày kết quả, các học sinh khác sẽ nhận xét và bổ sung ý kiến.

Bước 4: Kết luận và nhận xét: Giáo viên đánh giá kết quả của học sinh và từ đó dẫn dắt vào bài học mới: 'Toán học cung cấp ngôn ngữ và công cụ cho nhiều lĩnh vực khoa học. Trong các bài học trước, chúng ta đã sử dụng vectơ để biểu diễn lực và vận tốc, và áp dụng phép toán vectơ để tính hợp lực và tổng hợp vận tốc. Bài học này sẽ tiếp tục với khái niệm tích vô hướng giữa hai vectơ, liên quan đến công sinh bởi một lực trong Vật lý.'

3. Bài tập ứng dụng tích có hướng của hai vectơ trong không gian

Bài 1: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-2;2;1), B(1;0;2), C(-1;2;3). Tính diện tích tam giác ABC:

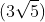
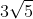
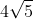
$(3\sqrt{5})$ $3\sqrt{5}$ $4\sqrt{5}$

D. 5/2

Bài 2: Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;0;0), B(0;1;0), C(0;0;1) và D(-2;1;-1). Tính thể tích của tứ diện ABCD:

A. 1

B. 2

C. 1/3

D. 1/2

Bài 3: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với các điểm A(2;-1;6), B(-3;-1;-4), C(5;-1;0). Tính bán kính của đường tròn nội tiếp tam giác ABC:

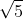
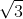
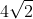
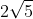
$\sqrt{5}$ $\sqrt{3}$ $4\sqrt{2}$ $2\sqrt{5}$

Bài 4: Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD với các điểm A(2;-1;1), B(5;5;4), C(3;2;-1), D(4;1;3). Tính thể tích của tứ diện ABCD:

A. 3

B. 4

C. 9

D. 6

Bài 5: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với các điểm A(1;0;0), B(0;0;1), C(2;1;1). Tính chiều cao của tam giác ABC từ đỉnh A:

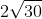
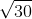
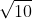
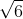
$2\sqrt{30}$ $\sqrt{30}$ $\sqrt{10}$ $\sqrt{6}$

Bài 6: Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.OAMN với các đỉnh S(0;0;1), A(1;1;0), M(m;0;0), N(0;n;0), với m>0, n>0 và tổng m+n=6. Tính thể tích của hình chóp S.OAMN:

A. 1

B. 2

C. 4

D. 6

Bài 7: Với các điểm A(1;-2;0), B(3;3;2), C(-1;2;2), D(3;3;1), tính thể tích của tứ diện ABCD.

A. 3

B. 4

C. 5

D. 6

Bài 9: Trong không gian với hệ tọa độ Oxyz, xét tứ diện ABCD với các điểm A(2;-1;6), B(-3;-1;-4), C(5;-1;0), D(1;2;1). Tính độ dài của đường cao AH từ A.

A. 5

B. 6

C. 7

D. 9

Bài 10: Trong không gian với hệ tọa độ Oxyz, xét các điểm A(1; 0; 0); B(0; 1; 0), C(0; 0; 1), D(1; 1; 1). Trong các mệnh đề sau, mệnh đề nào là sai?

A. Bốn điểm A, B, C, D không đồng phẳng.

B. Tam giác ABD là tam giác đều.

C. AB vuông góc với CD

D. Tam giác BCD là tam giác vuông.

Bài 11: Trong không gian Oxyz, xét các điểm A(0; 2; -2); B(-3; 1; -1);

C(4; 3; 0), D(1; 2; m). Xác định m để A, B, C, D đồng phẳng.

Một học sinh giải bài như sau:

Bước 1: Xác định AB→ = (-3;-1;1), AC→ = (4;1;2), AD→ = (1;0;m+2)

Bước 2: Tính tích có hướng [AB→, AC→] = (-3;10;1)

Bước 3: Tích vô hướng [AB→, AC→] ⋅ AD→ = 3 + m + 2 = m + 5

Kết luận: A, B, C, D đồng phẳng khi m = -5.

Bài giải trên có đúng không? Nếu sai, xác định sai ở bước nào?

A. Chính xác.

B. Sai ngay từ bước 1.

C. Sai ở bước 2.

D. Sai tại bước 3.

Bài 12: Cho hình chóp S.ABCD với các điểm A(-2;2;6), B(-3;1;8), C(-1;0;7), D(1;2;3). Gọi H là trung điểm của CD, SH vuông góc với mặt phẳng (ABCD). Nếu thể tích khối chóp S.ABCD là 27/2 thì có hai điểm S1, S2. Tìm tọa độ trung điểm I của đoạn S1S2.

A. (0; 1; 5)

B. (1; 0; 5)

C. (0; -1; -5)

D. (-1; 0; -5)

Bài 13: Trong hệ tọa độ Oxyz, cho bốn điểm A(-1;-2;4), B(-4;-2;0), C(3;-2;1), D(1;1;1). Hãy tính độ dài đường cao từ điểm D của tứ diện.

A. 3

B. 1

C. 2

D. 1/2

Nội dung từ Mytour nhằm chăm sóc khách hàng và khuyến khích du lịch, chúng tôi không chịu trách nhiệm và không áp dụng cho mục đích khác.

Nếu bài viết sai sót hoặc không phù hợp, vui lòng liên hệ qua email: [email protected]