1. Những kiến thức cơ bản cần nắm
Công thức giải phương trình bậc 2:
Áp dụng cho phương trình có dạng: ax² + bx + c = 0 với a khác 0
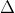
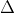
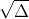
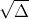
x₁ = x₂ = -b/2a
Kết luận: Phương trình luôn có hai nghiệm khác nhau
2. Định lý Viète đối với phương trình bậc 2
Khi học về phương trình bậc 2 hoặc phương trình bậc 2 một ẩn, không thể không nhắc đến định lý Viète.
Phương trình bậc 2 có dạng ax² + bx + c = 0 với a khác 0 có tối đa hai nghiệm, gọi là x₁ và x₂. Theo định lý Viète, có mối liên hệ giữa hai nghiệm và các hệ số của phương trình như sau:
x₁ + x₂ = -b/a
x₁ · x₂ = c/a
Khi giải các bài tập về phương trình bậc 2, bạn có thể sử dụng các mối liên hệ trên để hỗ trợ quá trình biến đổi và giải phương trình.
Ta có: x1 * x2 = P
x1 + x2 = S
Trong đó: x1 và x2 là nghiệm của phương trình bậc hai x2 - Sx + P = 0
- Trường hợp 1: Nếu a + b + c = 0 thì phương trình bậc hai có hai nghiệm x1 = 1 và x2 = c/a
- Trường hợp 3: Khi a - b + c = 0, phương trình bậc hai có hai nghiệm x1 = -1 và x2 = -c/a
2. Các dạng bài tập ứng dụng công thức nghiệm của phương trình bậc hai
- Dạng bài tập số 1: Phương trình bậc hai với một ẩn không có tham số
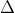
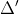
Ví dụ: xác định nghiệm của phương trình x2 - 3x + 2 = 0
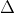
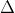
Vậy các nghiệm của phương trình trên là:
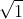
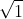
- Dạng bài tập 2: phương trình bậc hai với một ẩn có tham số
Ngoài dạng không có tham số, phương trình bậc hai với một ẩn có tham số cũng là một dạng bài tập quan trọng. Các bài tập này thường yêu cầu tìm điều kiện để hàm số có hai nghiệm, một nghiệm, hoặc không có nghiệm.
Dạng 3: xác định tham số m sao cho nghiệm của phương trình thỏa mãn điều kiện cho trước
- Chuyển phương trình về dạng ax2 + bx + c = 0 với a khác 0, kể cả khi có tham số m
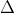
- Giải phương trình có chứa ẩn m như bình thường
- Dựa vào điều kiện nghiệm của bài toán để xác định giá trị của ẩn m
Ví dụ: Xác định giá trị của m trong phương trình 3x2 - 2(m + 1)x + 3m - 5 = 0 sao cho phương trình có một nghiệm gấp ba lần nghiệm còn lại. Tính các nghiệm trong trường hợp này
Giải bài toán:
Ta có phương trình: 3x2 - 2(m - 1)x + 3m - 5 = 0 (*)
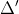
Do đó: (m + 1)2 - 3(3m - 5) > 0
Từ đó, suy ra m2 + 2m + 1 - 9m + 15 > 0
Suy ra m2 - 7m + 16 > 0
Suy ra (m - 7/2)2 + 15/4 > 0
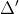
Gọi x1 và x2 là hai nghiệm của phương trình, theo định lý Viète ta có:
x1 + x2 = -b/a = 2(m + 1)/3 và x1 * x2 = c/a = (3m - 5)/3 (1)
- Theo bài toán, nghiệm của phương trình gấp 3 lần nghiệm kia, vì vậy không cần tính tổng quát khi giả định x2 = 3. x1 thay vào (1)
4x1 = 2(m +1)/3
3x1 = 3m - 5/3
Do đó: x1 = m + 1/6
x12 = (3m - 5)/9
Vậy: (m + 1/6)2 = (3m - 5)/9
Kết quả: m2 + 2m + 1/36 = (3m - 5)/9
Ta có: m2 + 2m + 1 = 4(3m - 5)
Kết quả: m2 - 10m + 21 = 0
Do đó: m = 3 hoặc m = 7
Trường hợp 1: Khi m = 3, phương trình (*) trở thành 3x2 - 8x + 4 = 0 với hai nghiệm x1 = 2/3 và x2 = 2, thỏa mãn điều kiện
Trường hợp 2: Khi m = 7, phương trình (*) trở thành 3x2 - 16x + 16 = 0 với hai nghiệm x1 = 4/3 và x2 = 4, thỏa mãn điều kiện
Kết luận: Khi m = 3, phương trình có hai nghiệm là 2/3 và 2
Khi m = 7, phương trình có hai nghiệm là 4/3 và 4
3. Các dạng bài tập thường gặp và bài tập tự luyện
Câu 1: Tìm nghiệm của phương trình 5x2 - x + 2 = 0
Hướng dẫn giải chi tiết:
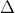 2
2
Phương trình trên không có nghiệm
Câu 2: Tìm nghiệm của phương trình: x2 - 4x + 4 = 0
Hướng dẫn chi tiết:
 2
2
Phương trình có nghiệm kép tại x = 2
Câu 3: Giải các phương trình x2 + 14x + 49 = 0 và x2 - 2x - 5 = 0
Hướng dẫn giải chi tiết:
Phương trình x2 + 14x + 49 = 0 có dạng hoàn chỉnh
 2
2Do đó, nghiệm của phương trình là:
x = -14/2 = -7
Vậy phương trình có nghiệm là:
x = -7
Phương trình: x2 - 2x - 5 = 0
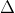 2
2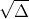
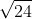
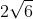
Do đó, nghiệm của phương trình là:
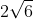
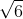
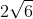
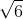
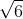
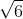
Câu 4: Xét phương trình -x2 + 2x + 20172017 = 0, không cần giải phương trình, hãy cho biết phương trình có bao nhiêu nghiệm?
Hướng dẫn chi tiết:
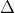 2
2Nhận xét: b2 > 0
ac = -20172017 < 0
Kết luận: -4ac > 0
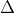 2
2Vì vậy, phương trình có hai nghiệm phân biệt
Do đó, phương trình có hai nghiệm phân biệt
Câu 5: Giải các phương trình bậc 2 sau đây:
a. 2x2 - 7x + 3 = 0
b. 3x2 + 2x + 5 = 0
c. x2 - 8x + 16 = 0
d. 3x2 + 5x + 2 = 0
Câu 6: Xác định giá trị của m để phương trình (2m -1) x2 - 2mx + 1 = 0 có nghiệm nằm trong khoảng (-1; 0)
Bài viết trên Mytour đã cung cấp thông tin chi tiết về công thức nghiệm phương trình bậc 2 và bài tập kèm đáp án. Cảm ơn bạn đã theo dõi bài viết.
