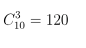1. Tổng quan về Nhị thức Newton
Nhị thức Newton là một định lý quan trọng trong toán học, liên quan đến việc khai triển hàm mũ của tổng và phân tích các đa thức bậc cao. Định lý này có nhiều ứng dụng trong toán học cũng như các lĩnh vực khác, bao gồm:
+ Tính tổ hợp và chỉnh hợp: Định lý Nhị thức Newton là công cụ hữu ích để tính số cách sắp xếp hoặc chọn k phần tử từ n phần tử mà không quan trọng thứ tự, với nhiều ứng dụng trong các bài toán tổ hợp và chỉnh hợp.
+ Dãy số: Định lý Nhị thức Newton cũng thường được sử dụng để chứng minh các thuộc tính của các dãy số, chẳng hạn như dãy số Fibonacci và dãy số Pascal.
+ Xác suất và thống kê: Trong lĩnh vực xác suất và thống kê, định lý Nhị thức Newton giúp tính toán xác suất và biểu diễn các phân phối xác suất, đặc biệt trong việc xác định xác suất của các biến ngẫu nhiên rời rạc.
+ Lý thuyết đồ thị: Định lý Nhị thức cũng được áp dụng để tính số lượng đồ thị con trong một đồ thị, có ứng dụng quan trọng trong lý thuyết đồ thị và các vấn đề mạng lưới.
Công thức Nhị thức Newton:
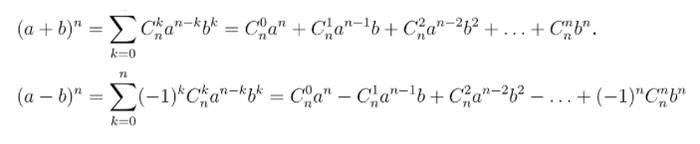

Các đặc điểm của công thức Nhị thức Newton:
+ Số lượng các hạng tử trong công thức là n + 1
+ Tổng của các số mũ a và b trong mỗi hạng tử luôn bằng số mũ của nhị thức: (n – k) + k = n
+ Hạng tử tổng quát của nhị thức là: Tk+1 = Cnk an-k bk ( Đây là hạng tử thứ k + 1 trong khai triển của (a + b)n )
+ Các hệ số nhị thức ở các vị trí đối xứng quanh trung tâm là bằng nhau.
2. Các loại bài toán với Nhị thức Newton
Bài toán xác định số hạng thứ k trong khai triển nhị thức Newton
Bước 1: Thực hiện khai triển nhị thức Newton để xác định số hạng tổng quát: Khai triển nhị thức Newton
.jpg)
Bước 2: Theo đề bài, giải phương trình hai số mũ phải bằng nhau. Số hạng chứa xm tương ứng với giá trị k thỏa mãn: np – pk + qk = m. Tính k bằng công thức: k = (m – np) / (p – q). Hệ số của số hạng chứa xm là: Cnk an-k bk với k đã tính. Nếu k không phải số nguyên hoặc k > n, thì trong khai triển không có xm, hệ số phải là 0.
Lưu ý: Để tìm hệ số của số hạng chứa xm trong khai triển P(x) = (a + bxp + cxq)n, hãy viết dưới dạng a0 + a1x + … + a2nx2n
Cách thực hiện như sau:
.jpg)
Xác định số hạng tổng quát khi khai triển các số hạng dạng bxp + cxq thành một đa thức theo lũy thừa của x. Dựa vào số hạng tổng quát của hai khai triển, ta có thể tính hệ số của xm.
Lưu ý: Để tìm hệ số lớn nhất trong khai triển nhị thức Newton
.png)
Hệ số lớn nhất cần tìm ứng với giá trị k lớn nhất sao cho bất phương trình được thỏa mãn.
Bài toán xác định hệ số trong khai triển nhị thức Newton.
Tìm hệ số của xk trong khai triển nhị thức Newton
Phương pháp tổng quát: Áp dụng công thức khai triển nhị thức Newton. Xác định số hạng chứa xk và tính toán hệ số tương ứng.
Ví dụ: Tìm hệ số của x3 trong khai triển của (2 + x)5
.png)
Với k = 3, hệ số của x3 được tính là: C35. 22 = 40
Bài toán tính tổng và chứng minh đẳng thức
Phương pháp giải:
Khai triển biểu thức: (a + b)n = C0n an + C1n an-1b + C2n an-2b2 + … + Cn-1n a bn-1 + Cnn bn
Từ đó, ta có thể chứng minh được điều cần thiết. Bằng cách thay a, b, n bằng các giá trị cụ thể, các đẳng thức sẽ được xác nhận. Đây là phương pháp ứng dụng định lý nhị thức Newton trong các bài toán tổ hợp.
Bài toán ứng dụng nhị thức Newton trong tổ hợp
Chọn một khai triển (a + x)n phù hợp, trong đó a là hằng số. Áp dụng các phép biến đổi đại số, đạo hàm hoặc tích phân nếu cần. Thay x bằng một giá trị cụ thể dựa trên điều kiện bài toán.
3. Một số bài tập ứng dụng liên quan
Câu 1. Xác định hệ số của các số hạng trong khai triển
a) (2x – 3y)17 có chứa x8y9
b) (3x – x2)12 có chứa x15
c) Có chứa x11
d) Có chứa x2
Hướng dẫn giải chi tiết
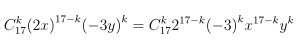
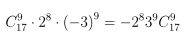
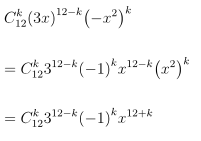
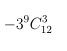
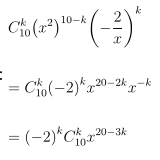
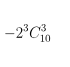
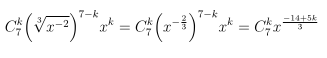
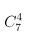
Câu 2. Tìm hệ số của x5 trong khai triển: P(x) = (1 + x) + 2(1 + x)2 + ... + 8(1 + x)8.
A. 630
B. 635
C. 636
D. 637
Giải thích: Các biểu thức (1 + x), (1 + x)2, …, (1 + x)4 không có số hạng chứa x5.
Hệ số của x5 trong khai triển 5(x + 1)5 là 5C55
Hệ số của x5 trong khai triển 6(x + 1)6 là 6C56
Hệ số của x5 trong khai triển 7(x + 1)7 là 7C57
Hệ số của x5 trong khai triển 8(x + 1)8 là 8C58
Do đó, tổng hệ số của x5 trong khai triển P(x) là 5C55 + 6C56 + 7C57 + 8C58 = 636
Chọn phương án C.
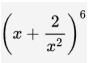
Hướng dẫn giải chi tiết:
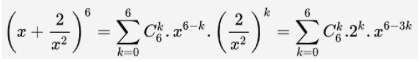
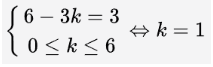
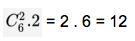
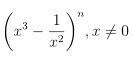
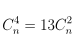
b) Tìm số hạng có chứa x2 trong khai triển
c) Tìm số hạng có chứa x8 trong khai triển
Hướng dẫn cách giải:
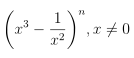
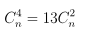
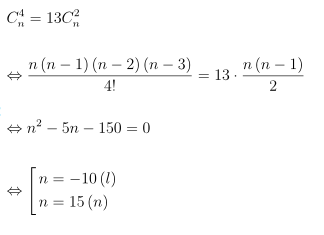
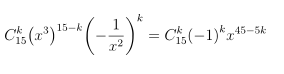
Số hạng chứa x10 tương ứng với điều kiện: 45 − 5k = 10 ⇔ k = 7.
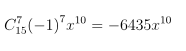
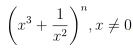
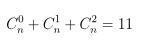
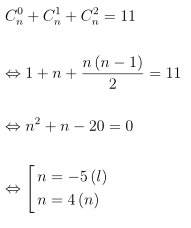
Số hạng tổng quát trong khai triển là: Để có số hạng chứa x2, ta có: 12 − 5k = 2 ⇔ k = 2.
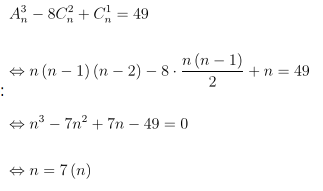
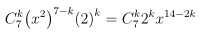
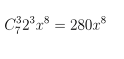
Câu 5. Tìm giá trị n là số nguyên dương sao cho trong khai triển (1 + x2)n, hệ số của x8 bằng 6 lần hệ số của x4.
Hướng dẫn giải quyết
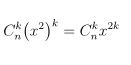
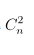
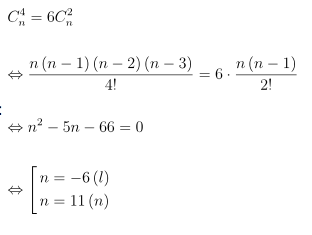
Do đó, giá trị n cần tìm là 11.
Câu 6.
a) Nếu tổng tất cả các hệ số trong khai triển (1 + x2)n bằng 1024, hãy xác định hệ số của x12.
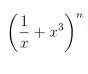
Hướng dẫn cách giải
a) Tổng các hệ số trong khai triển (1 + x2)n được cho là 1024. Để tìm hệ số của x12, ta đặt: P(x) = (1 + x2)n. Tổng các hệ số trong P(x) là P(1) = 2n. Vì tổng các hệ số trong (1 + x2)n là 1024, ta có: 2n = 1024 ⇔ n = 10.
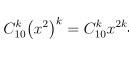
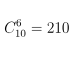
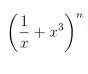
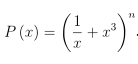 n
n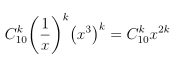
Số hạng chứa x6 tương ứng với: 2k = 6 ⇔ k = 3.