Công thức tính diện tích hình thoi và bài tập thực hành

Tính diện tích hình thoi là một trong những công thức cơ bản và thiết yếu trong toán hình học. Công thức này cho phép bạn tính diện tích của hình thoi một cách nhanh chóng và dễ dàng mà không cần đo đạc trực tiếp, từ đó áp dụng linh hoạt trong đời sống. Hãy cùng khám phá chi tiết về các công thức liên quan đến hình thoi và các bài tập thực hành cụ thể trong bài viết sau để hiểu rõ hơn nhé!

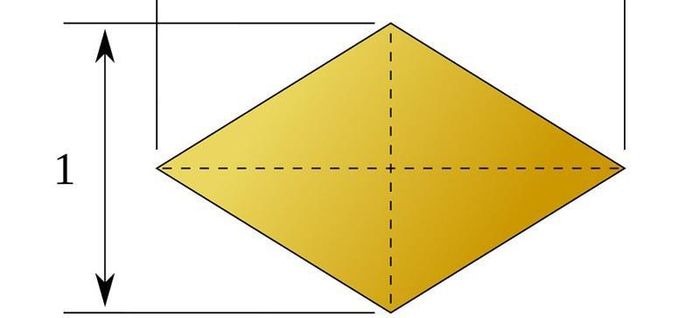
Hình thoi là một tứ giác có 4 cạnh bằng nhau, với hai cặp cạnh liền kề có độ dài tương đương, tạo thành hình bình hành và có 2 đường chéo cắt nhau vuông góc.

Một hình thoi cơ bản có những đặc điểm sau:

• Các góc đối của hình thoi là bằng nhau.

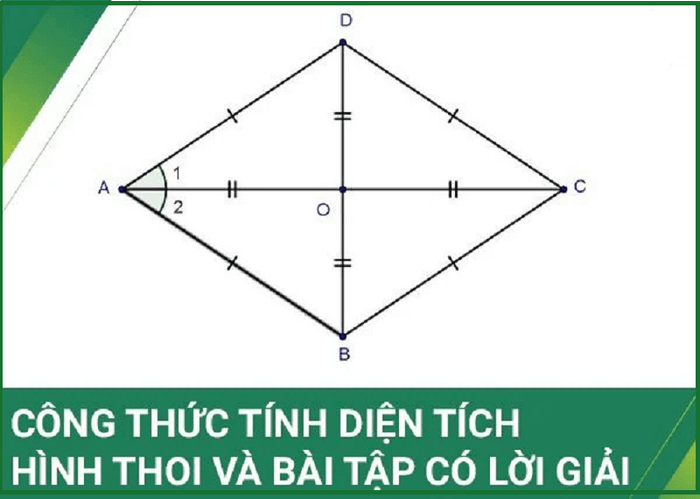
• Hai đường chéo của hình thoi vuông góc với nhau, và giao điểm của chúng chính là trung điểm của mỗi đường.

• Hai đường chéo cũng là đường phân giác trong hình thoi tại mỗi góc.

• Hình thoi có đầy đủ những đặc điểm của hình bình hành, với các cặp cạnh đối song song và bằng nhau.

• Các góc đối có hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Trước khi tìm hiểu về công thức tính diện tích hình thoi, bạn cần nắm một số dấu hiệu để nhận biết hình thoi như sau:

• Dấu hiệu đầu tiên: Hình thoi là tứ giác với 4 cạnh đều nhau.

• Dấu hiệu thứ hai: Tứ giác có hai đường chéo cắt nhau tại trung điểm.

• Dấu hiệu thứ ba: Tứ giác có hai đường chéo làm đường phân giác của bốn góc.

• Dấu hiệu thứ tư: Hình thoi là hình bình hành với hai cạnh kề bằng nhau.

• Dấu hiệu thứ năm: Hình bình hành có hai đường chéo vuông góc.

• Dấu hiệu thứ sáu: Hình bình hành có một đường chéo làm đường phân giác của một góc.

Dưới đây là các công thức tính diện tích hình thoi cơ bản cùng với ví dụ minh họa dễ hiểu nhất:

Diện tích hình thoi được tính bằng một nửa tích của độ dài hai đường chéo. Đường chéo là đoạn thẳng nối các đỉnh đối diện và hai đường chéo cắt nhau tại một điểm duy nhất và vuông góc với nhau.

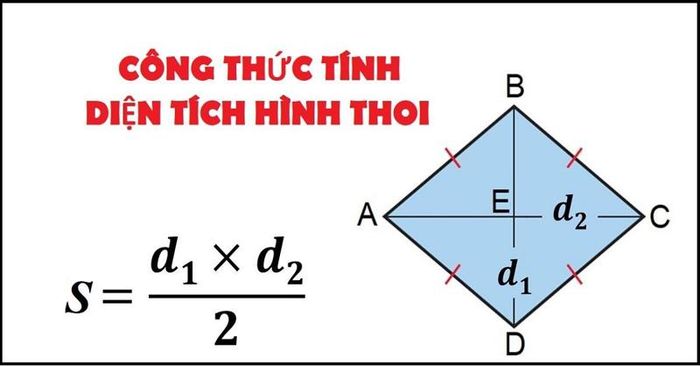
Công thức chi tiết như sau:

Ví dụ minh họa: Giả sử một hình thoi có độ dài hai đường chéo là d1 = 8 và d2 = 10. Vậy diện tích của hình thoi này sẽ được tính như thế nào?

Cách giải: Sử dụng công thức tính diện tích hình thoi: S = ½ x d1 x d2. Thay số vào, ta có: S = ½ x 8 x 10 = 40 cm²

Ngoài công thức tính diện tích hình thoi cơ bản, còn có phương pháp tính dựa trên hệ thức tam giác như sau:

3.2.1. Công thức 1

Nếu bạn nắm được số đo của một góc bất kỳ trong hình thoi, bạn có thể sử dụng hệ thức tam giác để tính diện tích theo công thức sau:

Ví dụ minh họa: Một hình thoi ABCD có góc A bằng 30 độ và cạnh bên dài 4cm. Yêu cầu tính diện tích S của hình thoi?

Cách giải: Diện tích hình thoi được tính theo công thức S = a^2 x sin A = 16 x sin 30 độ = 8cm2.

3.2.2. Công thức 2

Để tính diện tích hình thoi khi biết thông tin về các cạnh và các góc, bạn có thể áp dụng công thức tính diện tích hình chữ nhật hoặc hình tam giác.

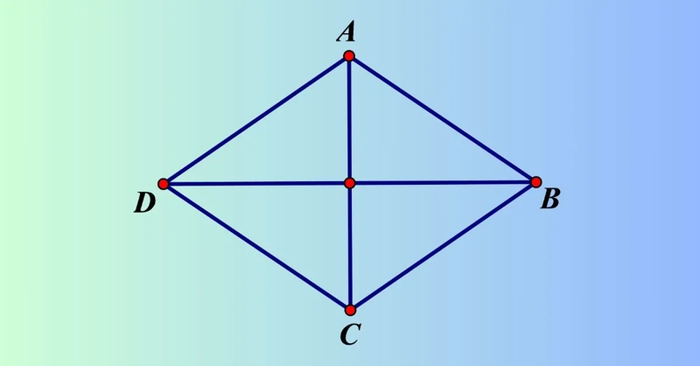
Lưu ý rằng các góc đối trong hình thoi luôn bằng nhau:

Ví dụ minh họa: Một hình thoi có cạnh dài 6cm và một góc là 60 độ. Vậy diện tích của hình thoi sẽ là bao nhiêu?

Cách giải: 

Sử dụng công thức tính diện tích tam giác: S = ½ x a x b x sin(C). Trong đó, a và b là hai cạnh của tam giác, còn C là góc giữa chúng.

Bởi vì hình thoi có các cặp góc đối bằng nhau, nên góc giữa hai cạnh là 60 độ. Đặt a = b = 6, vì cạnh của hình thoi đều nhau. Từ đó, diện tích của hình thoi được tính là: S = ½ x 6 x 6 x sin(60).

Nếu bạn biết chiều cao và cạnh đáy, bạn có thể sử dụng công thức dưới đây:

Ví dụ minh họa: Cho một hình thoi có chiều cao là 3cm và các cạnh AB, CD, BC, DA đều bằng 6cm. Tính diện tích của hình thoi này?

Cách giải: Áp dụng công thức tính diện tích hình thoi S = h x a = 3 x 6 = 18 cm2.

Dưới đây là một số bài tập thực hành về công thức tính diện tích của hình thoi, kèm theo lời giải chi tiết:

Có một mảnh vườn hình thoi với chiều dài đường chéo thứ nhất là 20m, và chiều dài đường chéo thứ hai bằng 3/4 chiều dài của đường chéo thứ nhất. Người nông dân đã trồng cà rốt trong khu đất này và mỗi m2 cho khoảng 5kg cà rốt. Vậy tổng số kg cà rốt mà người nông dân thu hoạch được là bao nhiêu?

Cách giải:

• Chiều dài đường chéo thứ hai = (20/4) x 3 = 15m.

• Diện tích của mảnh vườn hình thoi = (20 x 15)/2 = 150 m2.

• Tổng số kg cà rốt thu được từ mảnh vườn = 150 x 5 = 750kg.

Một khu đất hình thoi có tổng chiều dài của hai đường chéo là 400cm. Chiều dài của đường chéo thứ nhất chiếm 3/5 chiều dài của đường chéo thứ hai. Hãy tính diện tích của khu đất này?

Cách giải:

• Tổng số phần được chia từ hai đường chéo là 3 + 5 = 8 phần.

• Chiều dài đường chéo thứ hai = (400/8) x 5 = 250cm.

• Chiều dài đường chéo thứ nhất = 400 – 250 = 150cm.

• Diện tích khu đất hình thoi = (250 x 150)/2 = 18750 cm2.

Có một hình thoi CDEF với độ dài cạnh là 4cm, góc A = 35 độ. Tính diện tích của hình thoi CDEF?

Cách giải:

Sử dụng công thức tính diện tích hình thoi, với a = 4 và góc = 35 độ, ta có S = a² x sinA = 4² x sin(35°) = 9,177 (cm²).

Tính diện tích của một hình thoi với chiều cao 6cm và độ dài cạnh đáy là 80mm.

Cách giải:

• Chuyển đổi đơn vị: 80mm = 8cm.

• Độ dài cạnh đáy của hình thoi là 8cm.

• Áp dụng công thức tính diện tích hình thoi: S = a x h = 8 x 6 = 48cm².

Cho hình thoi có cạnh dài 15cm và một trong hai đường chéo dài 18cm. Hãy tính diện tích của hình thoi này?

Cách giải:

• Gọi hình thoi S1 có đường chéo d1 = 18cm, cạnh = 15cm và đường chéo d2. Theo tính chất hình thoi, hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm, tạo thành bốn tam giác vuông.

• Để tính chiều dài đường chéo d2, ta sử dụng định lý Pythagoras: d2 = 2 x √(15^2 – 9^2) = 2 x 12 = 24.

• Từ đó, diện tích hình thoi S1 = ½ (18 x 24) = 216 cm².

Trên đây là những thông tin về cách tính diện tích hình thoi cùng với các bài tập thực hành chi tiết nhất. Đây là một hình học đặc biệt, vì vậy cần nắm vững các công thức liên quan để có thể giải quyết chính xác và áp dụng tốt hơn trong thực tế.