Công thức tính diện tích và đường cao của tam giác vuông

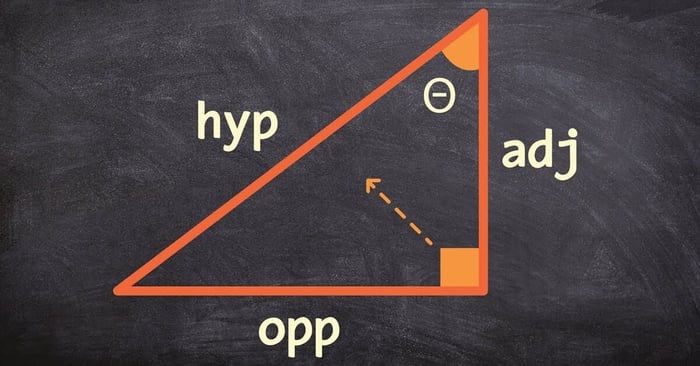
Cách tính diện tích và đường cao tam giác vuông là công cụ toán học quan trọng, giúp chúng ta xác định độ dài đường cao và diện tích của tam giác vuông một cách chính xác và hiệu quả. Ngoài ra, công thức này còn hỗ trợ tính toán các đại lượng như chu vi, đường chéo, góc… Dưới đây là chi tiết công thức tính diện tích và đường cao tam giác vuông.

Khái niệm tam giác vuông

Trước khi đi vào chi tiết cách tính diện tích và đường cao tam giác vuông, hãy tìm hiểu khái niệm về tam giác vuông. Đây là một hình học cơ bản và phổ biến trong toán học, với đặc điểm nổi bật là có một góc vuông chính xác là 90 độ. Đây là một trong những hình học cơ bản quan trọng, có nhiều ứng dụng trong lĩnh vực toán học và kỹ thuật. Các đặc tính quan trọng của tam giác vuông bao gồm:

• Hai góc còn lại khi cộng lại đúng 90 độ, tức là chúng là góc phụ của nhau.
• Bình phương của cạnh huyền (cạnh đối diện với góc vuông) bằng tổng của bình phương hai cạnh còn lại. Đây là Định lý Pythagoras, một trong những định lý quan trọng nhất trong toán học.
• Đường trung tuyến của cạnh huyền bằng một nửa chiều dài của cạnh huyền. Đây là một đặc tính độc đáo chỉ có trong tam giác vuông.

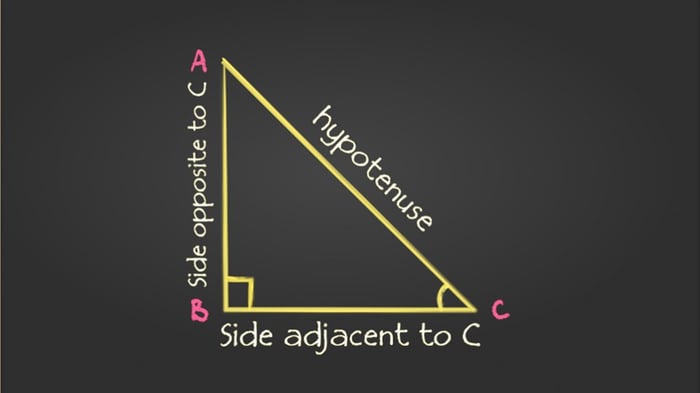
Nắm vững các tính chất và cách tính tam giác vuông giúp phát triển tư duy logic, khả năng giải quyết vấn đề và sáng tạo trong việc tìm giải pháp cho các bài toán toán học. Vì vậy, tam giác vuông không chỉ là một công cụ toán học mà còn là phương tiện để nâng cao kỹ năng toán học.

Cách tính độ dài đường cao và diện tích trong tam giác vuông

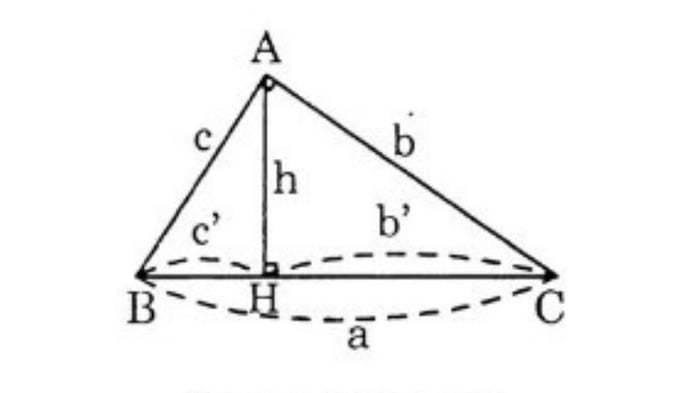
Tam giác vuông là một hình học đặc biệt với một góc vuông. Với cấu trúc đặc biệt này, chúng ta có công thức tính diện tích và độ dài đường cao của tam giác vuông. Trong đó:

• a,b,c là độ dài của các cạnh của tam giác vuông
• b′ là độ dài của đoạn thẳng vuông góc từ cạnh b đến cạnh huyền
• c′ là độ dài của đoạn thẳng vuông góc từ cạnh c đến cạnh huyền
• h là chiều cao từ đỉnh góc vuông A đến cạnh huyền của tam giác vuông

Để tính diện tích, chúng ta sử dụng công thức cơ bản.

S = 1/2 x a x b. 

Đường cao là một cạnh của tam giác vuông, nằm kề với góc vuông và chia tam giác thành hai tam giác nhỏ cùng vuông góc với nhau. Cho cạnh góc vuông là a và độ dài của đường cao là b. Đường cao có thể tính bằng công thức sau:

1. a2 = b2 + c2

2. b2 = a.b′ và c2 = a.c′

3. a.h = b.c

4. h2 = b′.c’

5. 1/h2 = 1/b2 + 1/c2

6. h = (S x 2)/c

Ví dụ về cách tính diện tích và đường cao trong tam giác vuông

Xét tam giác vuông ABC với góc vuông tại A và đường cao AH. AB có độ dài 16 cm và AC có độ dài 20 cm. Hãy tính diện tích và độ dài đường cao.

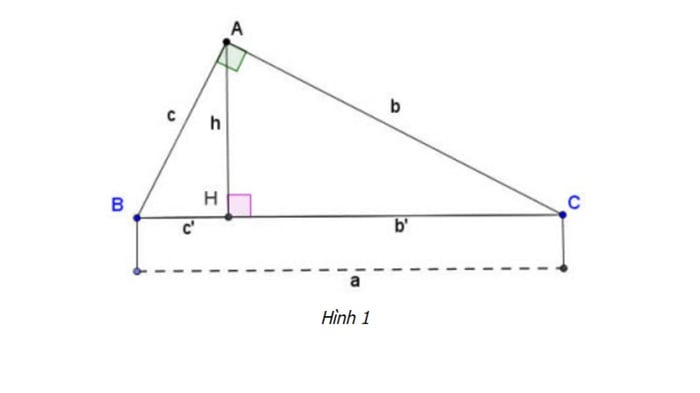
Để tính diện tích của tam giác này, bạn áp dụng công thức sau:

S = 1/2 x a x b = 1/2 x AB x AC = 1/2 x 16 x 20 = 260 cm2.

Tương tự, để tính độ dài đường cao AH, ta cần tính cạnh huyền BC trước. Áp dụng công thức sau:

BC^2 = AB^2 + AC^2 –>BC = √(AB² + AC²) = √(16^2 + 25^2) = 4

AH = (S x 2)/BC = (260 x 2)/4√41 = 130/√41. 

Ngoài ra, chúng ta có thể sử dụng nhiều công thức khác như a.h = b.c, và tương ứng AH . BC = AB . AC –> AH = (AB . AC) / BC = (16 x 20)/4√41 = 130/√41.

Có nhiều công thức khác nữa liên quan đến diện tích và đường cao của tam giác vuông. Quan trọng là áp dụng đúng công thức phù hợp với từng bài toán để giải quyết chính xác và hiệu quả.

Các công thức khác liên quan đến tam giác vuông

Ngoài các phương pháp tính diện tích và đường cao của tam giác vuông, còn tồn tại nhiều công thức khác liên quan đến hình học này. Dưới đây là một số công thức có thể tham khảo:

Định lý Pythagoras

Trong tam giác vuông, cạnh huyền bằng căn bậc hai của tổng bình phương hai cạnh góc vuông. Áp dụng định lý Pythagoras, ta có: c2 = a2 + b2. Nhờ đó, ta có thể suy ra các công thức sau:

• c = √(a² + b²)
• a = √(c² – b²)
• b = √(c² – a²)

Công thức Sin, Cos, và Tan

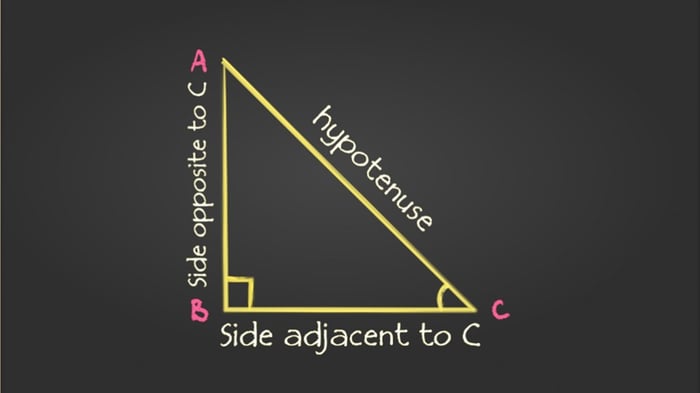
Trong tam giác vuông, Sin, Cos, và Tan là tỉ lệ giữa các cạnh với nhau. Các hàm số lượng giác này được áp dụng để tính toán các góc, độ dài các cạnh và các đại lượng khác trong tam giác vuông.

• Sin của một góc (được ký hiệu là sin) là tỷ lệ giữa chiều dài cạnh đối diện với góc đó và cạnh huyền của tam giác vuông.
• Cos của một góc (được ký hiệu là cos) là tỷ lệ giữa chiều dài cạnh kề với góc đó và cạnh huyền của tam giác vuông.
• Tan của một góc (được ký hiệu là tan) là tỷ lệ giữa chiều dài cạnh đối diện với góc đó và cạnh kề với góc đó của tam giác vuông.

Dựa trên các định lý Sin, Cos, và Tan trong tam giác vuông, chúng ta có thể áp dụng một số công thức liên quan.

• sin(góc) = a / c = 1 / cos(góc)
• cos(góc) = b / c = 1 / sin(góc)
• tan(góc) = a / b
• cot(góc) = 1 / tan(góc)
• sin α = cos β
• cos α = sin β
• tan α = cot β
• cot α = tan β

Các công thức trên cung cấp một nền tảng toán học vững chắc để nghiên cứu và giải quyết các vấn đề liên quan đến tam giác vuông trong nhiều ngữ cảnh và lĩnh vực khác nhau.

Ứng dụng của tam giác vuông trong thực tế

Như đã đề cập trước đó, tam giác vuông là một khái niệm cơ bản nhưng có sự ảnh hưởng sâu rộng đến nhiều khía cạnh. Dưới đây là các ứng dụng cụ thể của tam giác vuông.

Cách tính diện tích tam giác vuông trong lĩnh vực xây dựng và kiến trúc

Tam giác vuông có vai trò quan trọng trong nhiều lĩnh vực thực tiễn. Một trong những ứng dụng phổ biến nhất của tam giác vuông là trong kiến trúc và xây dựng. Khi kỹ sư hoặc nhà thiết kế cần đo đạc diện tích, ứng dụng của tam giác vuông rất quan trọng. Họ có thể dễ dàng và chính xác xác định diện tích cần thiết. Bạn cũng có thể thấy sự xuất hiện của tam giác vuông trong việc xây dựng các cấu trúc như cửa sổ, cánh cửa hay các góc mở của một căn phòng.

Áp dụng phương pháp tính tam giác vuông cũng giúp đo được diện tích thực tế mà một khu vực chiếm dụng. Điều này rất hữu ích trong việc lập kế hoạch và thiết kế không gian. Việc sắp xếp nội thất, thiết kế hướng dẫn lối đi thường sử dụng tam giác vuông làm nền tảng.

Cách tính diện tích tam giác vuông trong lĩnh vực kỹ thuật

Tam giác vuông có ứng dụng rộng rãi trong lĩnh vực kỹ thuật. Nó có thể được sử dụng để giải quyết nhiều vấn đề thực tế trong kỹ thuật.

• Chế tạo các thành phần máy móc, bộ phận yêu cầu độ chính xác cao, hoặc các thiết bị đo lường và kiểm tra.
• Định vị và đo đạc độ cao, độ sâu… của một khu vực hoặc địa hình.
• Xác định các mối liên hệ giữa các thành phần mạch, góc hướng và hướng dẫn dây dẫn, hoặc trong việc tính toán các thông số kỹ thuật cho các mạch điện.
• Đo lường, thiết kế và sản xuất các công cụ, thiết bị đo lường, và máy móc đo lường chính xác.

Cách tính diện tích tam giác vuông trong tự động hóa

Nguyên lý tam giác vuông đã được áp dụng rộng rãi trong tự động hóa và đã hình thành các giải pháp và ứng dụng trong ngành này. Ví dụ, nó hỗ trợ trong việc xác định hướng và vị trí cụ thể của robot trong không gian. Nhờ áp dụng nguyên lý này, các chuyên gia có thể tối ưu hóa điều khiển và định hướng robot một cách chính xác và hiệu quả.

Ngoài ra, việc xác định cấu trúc và bố trí các thành phần trong thiết kế robot cũng dựa trên các đặc tính của tam giác vuông. Khi thiết kế các bộ phận của robot, cần tối ưu hóa hiệu suất và chức năng của chúng. Việc lựa chọn góc và khoảng cách dựa trên nguyên lý tam giác vuông là điều cơ bản. Điều này giúp robot hoạt động hiệu quả và tiết kiệm năng lượng và tài nguyên.

Cách tính diện tích tam giác vuông trong vật lý và cơ học

Tam giác vuông và các hàm lượng giác được áp dụng trong nghiên cứu về các hiện tượng tự nhiên và cơ học chuyển động. Ví dụ, di chuyển của vật trên mặt phẳng có thể được dự đoán bằng các hàm lượng giác như sin, cos, và tan để tính toán quỹ đạo, tốc độ và gia tốc của vật trong các điều kiện khác nhau.

Ngoài ra, trong lĩnh vực vật lý, tam giác vuông được áp dụng để giải quyết các vấn đề liên quan đến cơ học và động lực học. Cụ thể, người ta thường sử dụng các phương trình và công thức lượng giác để phân tích và hiểu rõ hơn về các tương tác và hiện tượng vật lý.

Kết luận

Tóm lại, tam giác vuông đóng vai trò quan trọng trong mọi khía cạnh cuộc sống. Hiểu biết và áp dụng cách tính diện tích tam giác vuông giúp tăng hiệu quả của nhiều dự án đa lĩnh vực. Hơn nữa, việc nắm vững và áp dụng công thức tính diện tích tam giác vuông còn cải thiện khả năng phân tích. Người áp dụng cũng được nâng cao kỹ năng giải quyết vấn đề và sáng tạo trong đề xuất giải pháp cho những bài toán phức tạp. Đây là những kỹ năng quan trọng cho sự phát triển toàn diện của con người.

Hi vọng thông tin trên giúp bạn hiểu rõ hơn về hình học đặc biệt này. Ngoài ra, để tham khảo thêm các bài viết thú vị khác của Mytour, hãy truy cập các bài dưới đây.