
Bạn đang chuẩn bị cho kỳ thi sắp tới nhưng cảm thấy mơ hồ về hình cầu? Cảm thấy không biết nên bắt đầu từ đâu khi tính diện tích hình cầu và thể tích của nó? Đừng lo, hình cầu có thể gây khó khăn ban đầu, nhưng thông qua các công thức và cách tính đơn giản, chúng ta sẽ thấy rằng đây không phải là một nhiệm vụ khó khăn. Hãy cùng tìm hiểu cách tính diện tích cho hình cầu, một kiến thức quan trọng trong hình học không gian để chuẩn bị tốt nhất cho kỳ thi sắp tới của bạn.
Hình cầu và mặt cầu là gì?
Hình cầu là một khái niệm toán học quan trọng, mô tả một không gian ba chiều có hình dạng giống như một quả cầu, với điểm trung tâm cố định và các điểm trên bề mặt cách nhau một khoảng cách như nhau. Bề mặt cong của hình cầu tạo nên không gian liên tục, cong vút theo mọi hướng.
Mặt cầu là phần của bề mặt hình cầu, giới hạn không gian bên trong và bên ngoài của hình cầu. Điểm tâm của hình cầu (O) và bán kính (R) xác định vị trí của các điểm trên mặt cầu, mỗi điểm cách điểm tâm một khoảng bằng bán kính của hình cầu.
Ngoài ra, hình cầu có nhiều đặc tính đặc biệt như trục đối xứng qua tâm của nó. Mọi đường thẳng đi qua tâm hình cầu đều là trục đối xứng, khi quay hình cầu xung quanh trục này không làm thay đổi hình dạng của nó.
Ý nghĩa thực tiễn của diện tích hình cầu
Diện tích hình cầu, mặt cầu và thể tích khối cầu đóng vai trò quan trọng trong nhiều lĩnh vực khác nhau, từ toán học đến các ứng dụng thực tiễn trong cuộc sống hàng ngày.
Diện tích mặt cầu không chỉ là một khái niệm toán học mà còn có ý nghĩa rất quan trọng trong các lĩnh vực kỹ thuật và công nghệ. Việc xác định diện tích bề mặt của các vật thể hình cầu có thể được áp dụng trong thiết kế đồ họa, xây dựng, hay tính toán diện tích bề mặt của hệ quảng cáo và thiết kế sản phẩm. Việc hiểu và áp dụng diện tích mặt cầu cũng đóng vai trò quan trọng trong việc tính toán diện tích bề mặt của các hình dạng tròn trong lĩnh vực viễn thông và điện tử.
Thể tích khối cầu là một khái niệm rất quan trọng không chỉ trong toán học mà còn được ứng dụng rộng rãi trong các lĩnh vực kỹ thuật, địa chất, vật lý, y học và thiết kế công nghiệp. Ví dụ, trong công nghiệp, việc tính toán thể tích của các hộp chứa, bể chứa dung dịch và thiết kế các bánh răng, bi và các linh kiện máy móc đều dựa trên công thức tính thể tích khối cầu. Thậm chí, trong y học, việc xác định thể tích của khối u hay các cơ quan cơ thể cũng dựa trên nguyên lý này.
Mối liên kết giữa diện tích và thể tích hình cầu
Trong hình học, diện tích và thể tích của hình cầu là những khái niệm cơ bản thường xuất hiện trong nhiều bài toán. Cách tính này không chỉ đứng độc lập mà còn liên kết chặt chẽ với các công thức tính diện tích và thể tích của các hình khối khác như hình lập phương, hình trụ và hình hộp chữ nhật.
Khi giải các bài toán liên quan đến thể tích hình lập phương, hình trụ, hoặc hình hộp chữ nhật, việc áp dụng các công thức này có thể có nhiều phương pháp tính diện tích khác nhau. Điều này yêu cầu kết hợp các phương pháp tính diện tích của các hình cơ bản như tam giác, hình vuông, hoặc hình chữ nhật để đạt kết quả chính xác.
Đặc biệt, khi các hình dạng này kết hợp và giao nhau, việc áp dụng kiến thức về diện tích và thể tích của từng hình cơ bản giúp xác định kết quả cuối cùng một cách chính xác và linh hoạt. Kết nối và áp dụng kiến thức này giúp giải quyết nhiều bài toán phức tạp trong hình học không gian.
Tổng hợp các phương pháp tính thể tích mặt cầu và diện tích hình cầu
Công thức tính diện tích mặt cầu và thể tích khối cầu là những công thức căn bản mà học sinh thường cần học thuộc lòng trong môn toán hình học không gian. Đây là những công thức giúp tính toán diện tích và thể tích của hình cầu một cách nhanh chóng và chính xác.
Diện tích mặt cầu
Để tính diện tích chính xác của bề mặt hình cầu, bạn cần áp dụng công thức sau:
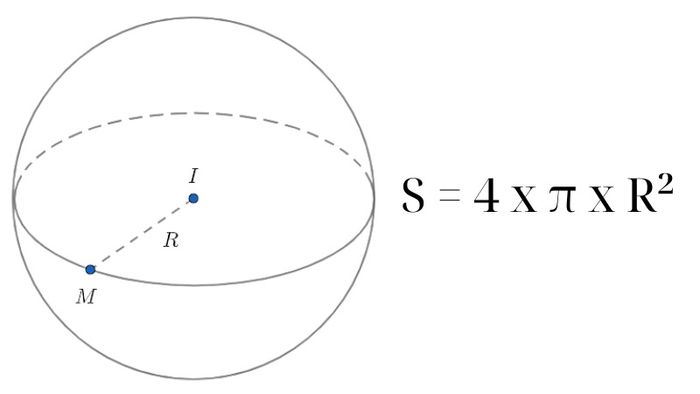
S = 4 x π x r² hoặc S = π x d²
Trong đó: S là diện tích bề mặt cầu, π là số Pi có giá trị khoảng 3.14, d là đường kính của bề mặt cầu và r là bán kính của bề mặt cầu.
Công thức này dựa trên việc diện tích bề mặt cầu bằng 4 lần diện tích của hình tròn lớn, với bán kính làm căn cứ chính. Để áp dụng công thức này, bạn có thể sử dụng bất kỳ giá trị cụ thể nào của bán kính hoặc đường kính của hình cầu.
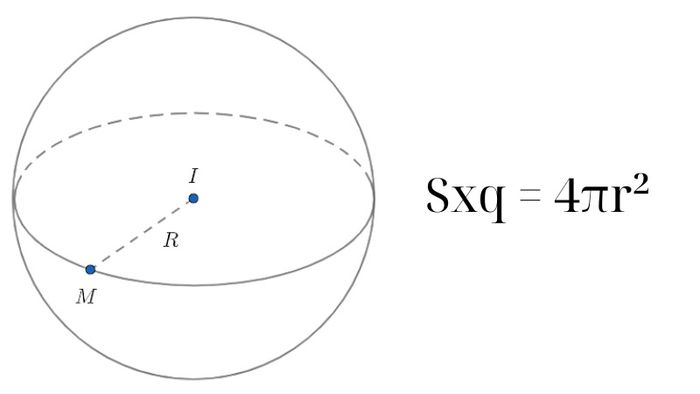
Diện tích bề mặt xung quanh của hình cầu
Để tính diện tích bề mặt xung quanh của một hình cầu, ta sử dụng công thức
Sxq = 4πr².
Đây là công thức giúp tính tổng diện tích bề mặt của hình cầu, bao gồm tất cả các bề mặt của nó.
Diện tích bề mặt xung quanh của hình cầu được ký hiệu là Sxq, được tính bằng cách nhân bán kính của hình cầu với chính nó (r²), sau đó nhân kết quả với 4π. Điều này tương đương với việc nhân bán kính với 2 rồi nhân với 2π, hoặc nhân bán kính với chính nó rồi nhân với π, từ đó đưa ra diện tích bề mặt xung quanh của hình cầu.
Thể tích của hình cầu
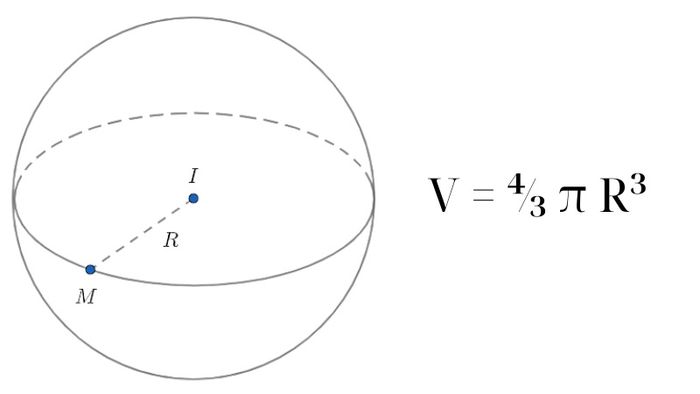
Khác với diện tích bề mặt của hình cầu, để tính thể tích của khối cầu một cách chính xác, ta sử dụng công thức sau:
V = ⁴⁄₃πr³
Ở đây: V là thể tích, r là bán kính của hình cầu.
Công thức này dựa trên việc thể tích của khối cầu là ba phần tư của số Pi nhân với lập phương của bán kính. Để sử dụng công thức này, chúng ta cần biết giá trị của bán kính hoặc đường kính của hình cầu. Sau đó, thay giá trị này vào công thức để tính toán thể tích của khối cầu một cách chính xác và nhanh chóng. Ngoài ra, đơn vị của thể tích thường được đo bằng đơn vị khối như mét khối (m³) hoặc centimet khối (cm³).
Tập hợp một số bài tập
Dưới đây là một số bài tập có đáp án để bạn có thể áp dụng công thức tính diện tích bề mặt cầu và thể tích khối cầu một cách thành thạo.
Bài 1
Cho một đường tròn có tâm là O, bán kính của nó là 9m. Vậy diện tích của hình cầu này là bao nhiêu?
Hướng dẫn
Bước 1: Ghi nhớ công thức
Hãy đảm bảo bạn đã ghi chép các công thức tính diện tích bề mặt của hình cầu và thể tích khối cầu. Việc này sẽ giúp bạn dễ dàng áp dụng chúng vào bài tập một cách chính xác.
Bước 2: Xác định bán kính
Nếu đề bài cung cấp bán kính thì bạn có thể đi thẳng đến bước tiếp theo. Tuy nhiên, nếu chỉ có thông tin về đường kính, hãy nhớ rằng bán kính bằng nửa đường kính. Ví dụ, khi đường kính là 20cm, bán kính sẽ là 10cm.
Bước 3: Sử dụng công thức
Sau khi xác định được bán kính, thay giá trị này vào công thức tính diện tích hình cầu S=4πR^2. Bằng cách tính toán theo công thức này, bạn sẽ thu được kết quả chính xác cho bài toán.

Phương pháp thực hiện:
Để tính diện tích bề mặt của hình cầu khi đã biết bán kính của nó, bạn hãy áp dụng công thức S = 4πR².
Trong trường hợp này, bán kính của hình cầu là 9m, do đó diện tích bề mặt của hình cầu sẽ là:
S = 4 x 3,14 x 9^2 = 1017.36 m2
Bài 2
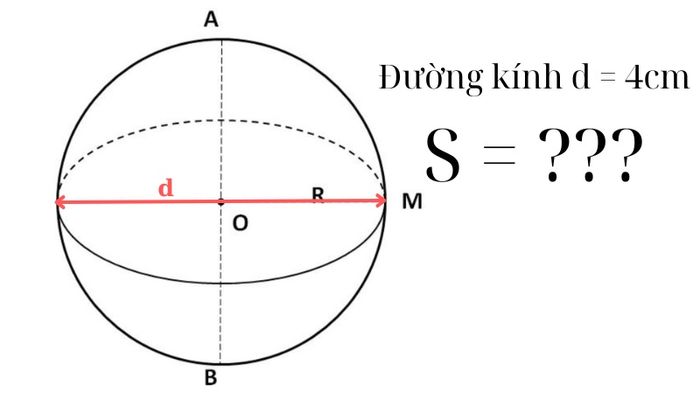
Nếu một hình cầu có đường kính d là 4cm, thì diện tích bề mặt của hình cầu là (cm2)
A – 9π
B – 36π
C – 16π
D – 12π
Cách làm:
Trước hết, với một hình cầu có đường kính d = 4, ta biết rằng bán kính của nó sẽ là R = d/2 = 2 (cm)
Tiếp theo, ta áp dụng công thức: S=4πR^2. Sau khi thay giá trị vào, ta có
S = 4πR^2 = 4π2^2 = 16 π (cm2)
Vậy đáp án đúng là C – diện tích hình cầu là 16π (cm2)
Bài số 3
Cho một khối cầu có đường kính là 2cm. Hãy tính thể tích của khối cầu này.
Hướng dẫn chi tiết
Để tính thể tích của một quả cầu, bạn có thể sử dụng công thức sau:
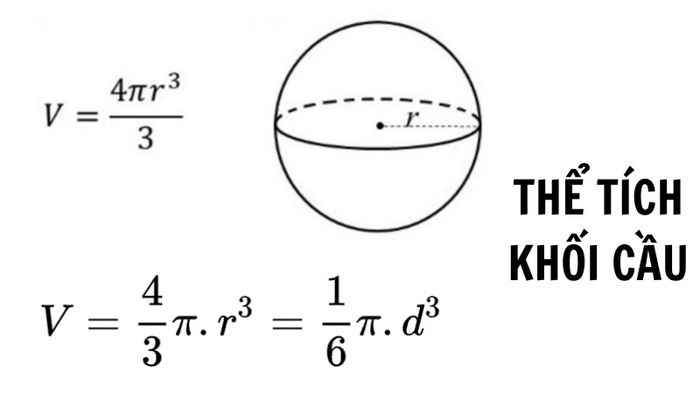
Bước 1: Viết công thức tính thể tích của hình cầu lên giấy: V = ⁴⁄₃π.r³.
Bước 2: Đọc đề, nếu cho bán kính thì ghi lại; nếu cho đường kính, sử dụng công thức V = 1⁄6π.d³ hoặc chia đường kính cho 2 để có bán kính, sau đó áp dụng công thức từ bước trước. Nếu đề chỉ cung cấp diện tích mặt cầu (S), chia S cho 4π và lấy căn bậc hai để có bán kính (r = √(S/4π)).
Bước 3: Sau khi có bán kính, tính lũy thừa bậc ba của bán kính bằng cách nhân bán kính với chính nó ba lần.
Bước 4: Thay bán kính lũy thừa vào công thức V = ⁴⁄₃πr³ để tính thể tích của hình cầu.
Bước 5: Nhân kết quả tính được với π (số pi) để có giá trị cuối cùng của thể tích hình cầu.
Phương pháp giải quyết
Để tính thể tích của hình cầu có đường kính d = 4 cm, ta bắt đầu bằng cách xác định bán kính r của hình cầu. Bán kính r được tính bằng nửa đường kính, tức là:
r = d/2 = 1 (cm)
Sau đó, áp dụng công thức tính thể tích của hình cầu vào công thức V = ⁴⁄₃πr³, ta có:
V = ⁴⁄₃πr³ = 4/3.3,14.(1)³ = 4,18 (cm³).
Tổng kết
Trong bài viết này của Mytour, chúng ta đã đi sâu vào việc khám phá công thức tính diện tích hình cầu và thể tích khối cầu. Việc hiểu sâu hơn về những công thức đơn giản nhưng quan trọng này không chỉ giúp chúng ta hiểu rõ hơn về hình học không gian mà còn áp dụng rộng rãi trong thực tế. Việc tính toán diện tích và thể tích của hình cầu không chỉ là kiến thức cần thiết trong lĩnh vực toán học để bạn vượt qua kỳ thi mà còn hữu ích trong các lĩnh vực kỹ thuật, công nghiệp và nhiều lĩnh vực khác, cũng như là giải pháp sáng tạo trong cuộc sống hàng ngày.
