Bài viết dưới đây chúng tôi sẽ giải đáp cho bạn về công thức tính đường chéo hình lập phương & Ví dụ minh họa.

I. Đôi nét về hình lập phương
Hình lập phương được biết đến như là một dạng hình học không gian ba chiều đã được tạo ra từ tổng cộng sáu mặt phẳng vuông góc với nhau và những mặt phẳng này đều sẽ có cùng diện tích và hình dạng với nhau. Hình học này còn được gọi với cái tên gọi khác là khối lập phương hoặc là hình khối đều. Mỗi mặt của một hình lập phương đều là một hình vuông, và độ dài cạnh của mặt phẳng hình vuông trong hình lập phương là đồng đều với nhau. Cạnh của hình lập phương sẽ được ký hiệu là “a”, và diện tích của một mặt trong hình lập phương sẽ là a², diện tích toàn bộ của hình lập phương sẽ là 6a². Thể tích của hình lập phương sẽ có công thức là a³.

II. Thảo luận về hình lập phương
1. Khái niệm về đường chéo của hình lập phương
Đường chéo trong hình lập phương là đoạn thẳng nối hai đỉnh không thuộc cùng một cạnh. Hình lập phương có thể coi là một trường hợp đặc biệt của hình tứ diện đều.
2. Công thức tính đường chéo hình lập phương
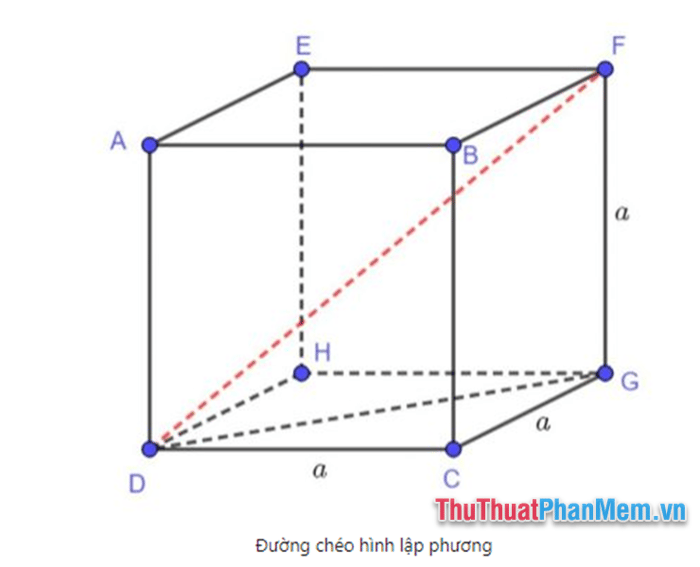
Khi quan sát hình lập phương ABCD.A’B’C’D’ với các cạnh bằng nhau được biểu diễn là a. Áp dụng định lý Pythagoras, chúng ta có thể tính được đường chéo của một mặt là:
Đường chéo AC của mặt ABCD = a√2
Đường chéo của hình lập phương có công thức là AC’ = √(AC² + CC’²) = √(2a² + a²) = a√3
Để tính độ dài đường chéo của hình lập phương, ta sử dụng 2 công thức phổ biến nhất:
+ Để tính độ dài đường chéo của hình lập phương, sử dụng công thức: D = a√3
+ Để tính độ dài đường chéo của mặt bên hình lập phương, sử dụng công thức: d = a√2
Ký hiệu trong công thức tính đường chéo trong hình lập phương là:
- a là độ dài cạnh của hình lập phương
- D là đường chéo trong hình lập phương
- d là đường chéo của mặt bên hình lập phương
3. Ví dụ
Cho một hình lập phương có cạnh a = 3cm. Hỏi độ dài đường chéo của hình lập phương là bao nhiêu?
Lời giải:
Theo như ký hiệu trên hình vẽ, AC là đường chéo của mặt hình vuông ABCD, và AC’ là đường chéo của hình lập phương ABCD.A’B’C’D’.
Xét tam giác ABC vuông tại B:
AB² + BC² = AC²
⇔ 3² + 3² = AC²
⇔ 18 = AC²
=> AC= 3√2 (centimet)
Với hình lập phương ABCD.A’B’C’D’, đường chéo CC' vuông góc với mặt phẳng (ABCD)
=> CC' là đoạn thẳng vuông góc với AC
Xét tam giác ACC' chúng ta có:
AC bình phương cộng với CC' bình phương bằng AC' bình phương
⇔ (3√2) bình phương cộng với 3 bình phương bằng AC' bình phương
⇔ 27 bằng AC' bình phương
=> AC' bằng 3√3 (centimet)
Trong bài viết này, chúng tôi đã hướng dẫn cách tính đường chéo của hình lập phương và minh họa bằng ví dụ. Chúc bạn có một ngày thú vị!
