Công thức tính hoán vị, chỉnh hợp và tổ hợp đầy đủ

Khá nhiều người khi tiếp xúc với công thức chỉnh hợp, hoán vị và tổ hợp có thể nhầm lẫn khái niệm, cũng như phân biệt công thức chính xác. Vì thế, Mytour đã tổng hợp bài viết này để giải thích rõ hơn về ba công thức toán học này. Bên cạnh đó, chúng tôi cũng có ví dụ minh họa ở mỗi công thức để giúp bạn hiểu rõ hơn.

Khái niệm về Hoán vị là gì?

Hoán vị là một khái niệm quan trọng trong toán học và lý thuyết đồ thị. Nó được dùng để mô tả cách mà các phần tử của một tập hợp có thể được sắp xếp lại hoặc đổi chỗ với nhau để tạo ra một sự thay đổi trong cấu trúc ban đầu. Đây là một khía cạnh của lý thuyết tổ hợp, nơi nghiên cứu về sự sắp xếp, kết hợp và chọn lựa của các phần tử trong một tập hợp hữu hạn.

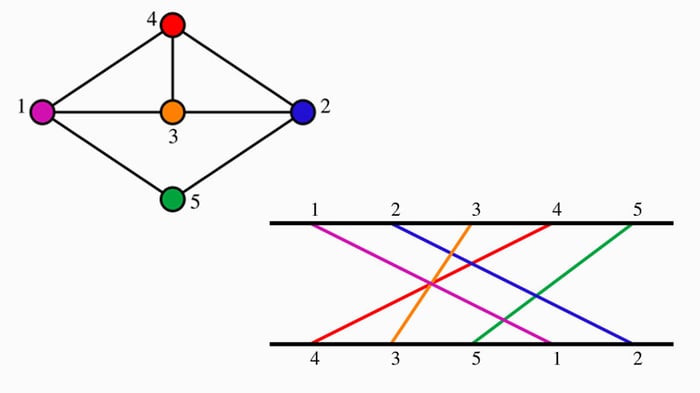
Một hoán vị của một tập hợp bao gồm các phần tử được sắp xếp theo một thứ tự nhất định. Điểm khác biệt giữa hoán vị và các khái niệm khác như tổ hợp và các phần còn lại của tập hợp là mỗi phần tử chỉ xuất hiện đúng một lần trong mỗi hoán vị. Điều này tạo ra nhiều hoán vị khác nhau tùy thuộc vào số phần tử trong tập hợp.

Ví dụ, với một tập hợp A có N phần tử với N lớn hơn hoặc bằng 0. Mỗi cách sắp xếp của N phần tử theo một vị trí cụ thể sẽ được gọi là hoán vị của N phần tử. Số lượng hoán vị của N phần tử thường được ký hiệu là Pn.

Định nghĩa về Tổ hợp

Trong bộ ba công thức chỉnh hợp, tổ hợp và hoán vị, tổ hợp và hoán vị có định nghĩa tương đương. Điều này dễ khiến nhiều người nhầm lẫn và sử dụng sai trong tính toán. Để hiểu rõ hơn về điều này, Mytour đã tổng hợp khái niệm chính xác của tổ hợp.

Tổ hợp là cách các phần tử có thể được sắp xếp, kết hợp và chọn từ một tập hợp hữu hạn để tạo ra các cấu trúc mới. Nói cách khác, đây là cách chúng ta chọn ra các phần tử từ một tập hợp X mà không phân biệt vị trí của chúng. Đặc biệt, trong một số trường hợp đặc biệt, bạn có thể đếm được số tổ hợp.

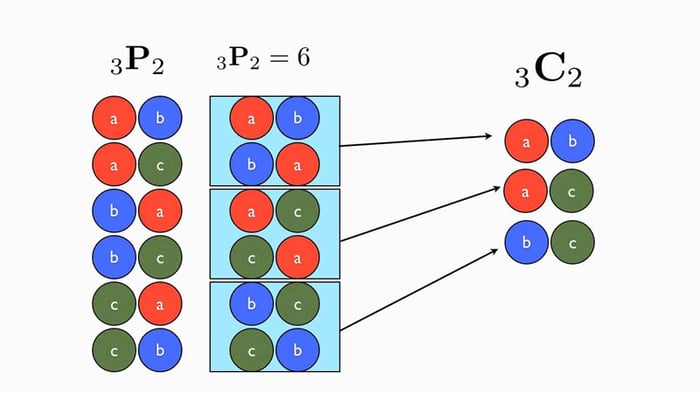
Ngoài ra, trong tổ hợp, các khái niệm như tổ hợp chập k và tổ hợp nhị thức đều có vai trò quan trọng. Tổ hợp chập k mô tả cách chọn k phần tử từ một tập hợp. Trong khi đó, tổ hợp nhị thức thường được sử dụng để đếm số cách khác nhau mà một sự kiện có thể xảy ra.

Áp dụng vào toán học, chúng ta sẽ dễ hình dung hơn rằng một tập hợp con gồm k phần tử từ một tập hợp a > 0 sẽ được coi là một tổ hợp chập k của a.

Khái niệm về Chỉnh hợp là gì?

Tiếp theo, chúng ta sẽ cùng nhau tìm hiểu chi tiết hơn về khái niệm công thức chỉnh hợp trong toán học. Chỉnh hợp mô tả cách các phần tử trong một tập hợp có thể được chọn và sắp xếp theo một thứ tự cụ thể để tạo ra các cấu trúc khác nhau. Khác với hoán vị, chỉnh hợp không yêu cầu sử dụng tất cả các phần tử, mà chỉ một phần của chúng. Chỉnh hợp thường được ký hiệu là A(n,k), với n là số phần tử trong tổ hợp và k là số phần tử được chọn.

Công thức toán học về chỉnh hợp có nhiều ứng dụng thực tế. Ví dụ, trong mật mã học, nó có thể được dùng để xác định số lượng khóa mã hóa khác nhau. Trên lĩnh vực quản lý dự án, chỉnh hợp có thể áp dụng để xác định số cách khác nhau để lập lịch công việc hoặc xếp hàng tác vụ. Ngoài ra, trong xác suất học, chỉnh hợp thường xuất hiện khi xem xét các sự kiện có thứ tự cụ thể.

Các mối quan hệ giữa công thức chỉnh hợp, hoán vị và tổ hợp là gì?

Dựa trên những khái niệm đã được Mytour giới thiệu, chúng ta thấy được mối liên kết sâu sắc giữa tổ hợp, hoán vị và chỉnh hợp. Một chỉnh hợp chập k của n sẽ được hình thành từ 2 bước cơ bản để xác định.

(1) Đầu tiên, bạn cần lấy một tổ hợp chập k từ n phần tử.

(2) Sau đó, bạn sẽ thực hiện hoán vị k phần tử để tạo thành một chỉnh hợp chập k của n.

Có thể nói, những công thức chỉnh hợp, hoán vị và tổ hợp thường xuyên xuất hiện trong các bài toán THPT. Đặc biệt, chúng thường được đưa vào đề thi tốt nghiệp THPT trong những năm gần đây. Điều này làm cho việc hiểu rõ bản chất của chúng và áp dụng công thức đúng cách trở nên cực kỳ quan trọng.

Hướng dẫn quy tắc đếm đơn giản nhất cho hoán vị, tổ hợp và chỉnh hợp

Tiếp tục nội dung, Mytour sẽ chia sẻ với bạn những quy tắc đếm cực kỳ quan trọng để áp dụng cho các công thức hoán vị, tổ hợp và chỉnh hợp. Mỗi khái niệm sẽ có một quy tắc đếm riêng biệt, vì vậy đừng bỏ lỡ phần nội dung quan trọng này.

Quy tắc đếm hoán vị

Như chúng ta đã biết, hoán vị là việc sắp xếp một tập hợp k phần tử. Từ một tập hợp này, ta có thể tạo ra hoán vị của a phần tử bằng hai thao tác đơn giản như sau: 

(1) Bước đầu tiên, chọn phần tử đầu tiên và thực hiện cộng tổng n cách.

(2) Tiếp theo, chọn phần tử tiếp theo và thực hiện công thức (n-1) theo cách sắp xếp hoán vị.

(3) Tiếp tục như vậy cho đến khi chọn các phần tử tiếp theo và áp dụng công thức chung là (a-1).

Lưu ý: Trong những trường hợp đặc biệt khi n = a, chúng ta sẽ sử dụng công thức P(n) = n! để tính số hoán vị không trùng nhau. Trường hợp nếu a < n, số hoán vị sẽ được tính theo công thức P(n,a) = n!(n-a)!.

Quy tắc đếm tổ hợp

Trước khi bạn tìm hiểu về công thức chỉnh hợp, hoán vị và tổ hợp, bạn cần hiểu về quy tắc đếm của chúng. Tiếp theo, chúng ta sẽ cùng tìm hiểu về quy tắc đếm tổ hợp. Tổ hợp có phương pháp đếm đơn giản nhất và ai cũng có thể áp dụng sau khi đọc chia sẻ này.

Chúng ta sẽ có một tập hợp X gồm n phần tử với n > 0. Tiếp theo, chúng ta sẽ có một tổ hợp chập k với các phần tử bất kỳ từ tập hợp X. Điều kiện là 0 ≤ k ≤ n và k ∈ n. Từ đó, chúng ta có công thức quy tắc đếm tổ hợp là n!(n-k)!.

Quy tắc đếm chỉnh hợp

Có thể nói, công thức đếm hoán vị áp dụng chung cho cả tổ hợp và chỉnh hợp. Vì vậy, nếu bạn đã hiểu rõ hoán vị, cách tính tổ hợp và chỉnh hợp cũng rất đơn giản. Cụ thể trong phần này là quy tắc đếm chỉnh hợp.

Quy tắc đếm chỉnh hợp áp dụng cho tập hợp lớn X với n ≥ 1, n là số phần tử trong tập hợp, k là số lượng phần tử được chọn và sắp xếp. Điều kiện là 1 ≤ k ≤ n và k ∈ n. Từ đó, công thức quy tắc đếm chỉnh hợp là n!k!(n-k)!.

Công thức chỉnh hợp, tổ hợp, hoán vị và ví dụ minh họa

Sau khi đã tìm hiểu về các khái niệm cơ bản, bây giờ chúng ta sẽ đi sâu vào nội dung quan trọng nhất của bài viết này. Cùng Mytour học các công thức tính chỉnh hợp, tổ hợp và hoán vị nhé. Đương nhiên, để hiểu thực sự bạn cần thực hành cùng một số ví dụ minh họa cụ thể.

Công thức hoán vị

Công thức tính hoán vị của n phần tử rất đơn giản. Chúng ta biết ký hiệu của hoán vị là P(n). Vì vậy, công thức tính hoán vị là P(n) = n!. Ở đây, n! biểu thị cho giai thừa của n, nghĩa là tích của tất cả các số nguyên từ 1 đến n.

Ví dụ: Một ví dụ cụ thể là chúng ta có một tập hợp gồm 4 phần tử X = {A, B, C, D} = {4, 3, 2, 1}. Vậy từ tập hợp X, chúng ta có thể sắp xếp bao nhiêu số khác nhau gồm 4 chữ số?

Đáp án: Bạn áp dụng công thức P(n) = n! = P(4) = 4! = 4×3×2×1= 24. Từ đó, chúng ta có 24 cách sắp xếp khác nhau từ tập hợp X.

Công thức tổ hợp

Đối với công thức tính tổ hợp sẽ phức tạp hơn công thức chỉnh hợp và hoán vị. Cụ thể, công thức tính tổ hợp của n phần tử chọn k phần tử, ký hiệu là C(n,k): C(n,k) = n! / (k!(n-k)!) = (n(n-1)(n-2)…(n-k+1))/k!. Ở đây, n! là giai thừa của n, k! là giai thừa của k và (n-k)! là giai thừa của n-k.

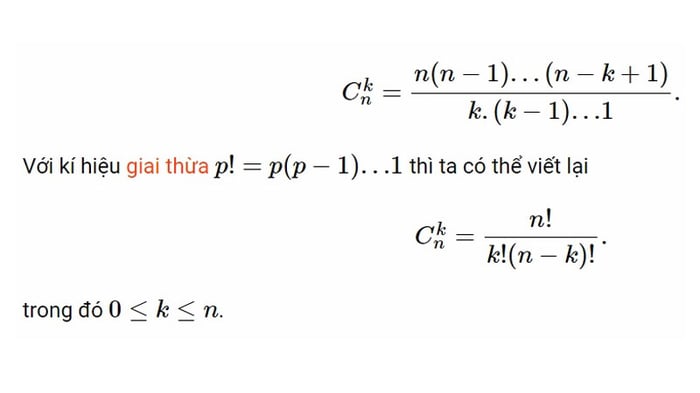
Ví dụ, nếu bạn có một tập hợp gồm 5 phần tử {A, B, C, D, E} = {5, 4, 3, 2, 1} và bạn muốn chọn 3 phần tử, số tổ hợp của chúng là: C(5,3) = 5! / 3!(5−3) = (5×4×3) / (3×2×1) = 10.

Công thức chỉnh hợp

Công thức tính chỉnh hợp cũng khá đơn giản, bạn chỉ cần đọc hiểu những điều kiện trong bài toán với n phần tử chọn k phần tử và sắp xếp theo một thứ tự cụ thể. Áp dụng công thức tính chỉnh hợp như sau: A (n,k) = n! / (n-k)! =  n(n-1)(n-2)…(n-k+1).

Ví dụ: Bài toán cho một tập hợp gồm 6 phần tử {A, B, C, D, E, F} = {6, 5, 4, 3, 2, 1} và bạn muốn chọn 4 phần tử và sắp xếp chúng theo một thứ tự cụ thể, số chỉnh hợp của chúng là: A(6,4) = 6! / (6-4)! = (6×5×4×3×2×1) / (2×1) = 360. Do đó, có 360 cách chọn và sắp xếp 4 phần tử từ tập hợp này.

Kết luận

Như vậy, Mytour đã chia sẻ cho bạn các thủ thuật tính toán công thức chỉnh hợp, tổ hợp và hoán vị. Các công thức này không quá phức tạp để áp dụng, nhưng bạn cần hiểu rõ về bản chất và phân biệt chúng.