Việc hiểu rõ công thức tính thể tích khối chóp không chỉ giúp bạn giải quyết nhanh chóng các bài toán hình học mà còn có thể áp dụng vào thực tế cuộc sống. Bài viết này, Mytour sẽ chia sẻ các công thức tính thể tích khối chóp đều và không đều, đồng thời tổng hợp 12 bài tập mẫu kèm theo lời giải chi tiết giúp bạn dễ dàng nắm bắt và áp dụng.
Khối chóp là gì?
Khối chóp là một đa diện có các mặt bên là các tam giác, tất cả giao nhau tại một đỉnh. Đáy của khối chóp là một đa giác. Chiều cao của khối chóp là khoảng cách vuông góc từ đỉnh xuống mặt đáy.
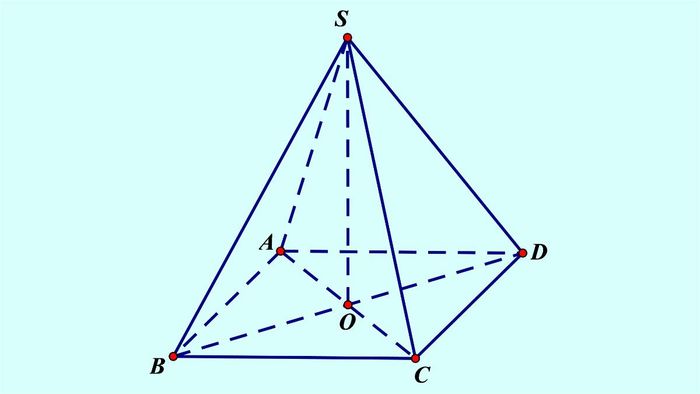
Khối chóp là một loại bài toán hình học phổ biến và có nhiều ứng dụng trong đời sống thực tế. Do đó, việc nắm vững công thức tính thể tích khối chóp là rất quan trọng.
Đặc điểm của khối chóp
Khối chóp có các đặc điểm sau:
- Khi các cạnh bên của khối chóp có độ dài đồng đều, chân của đường cao chính là tâm của đường tròn đi qua tất cả các đỉnh của đa giác đáy.
- Khi các mặt bên tạo với đáy các góc bằng nhau, chân của đường cao chính là tâm của đường tròn tiếp xúc với tất cả các cạnh của đa giác đáy.
- Nếu một mặt bên vuông góc với đáy, chân của đường cao sẽ là giao điểm của đường vuông góc từ đỉnh xuống đáy, thuộc mặt bên này.
- Khi hai mặt bên vuông góc với đáy, đường giao tuyến giữa hai mặt bên cũng sẽ vuông góc với đáy.
Công thức tính thể tích cho khối chóp
Công thức tính thể tích của khối chóp là: V = 1/3 x S x h
Trong đó:
- h: là chiều cao của khối chóp, là đoạn thẳng vuông góc từ đỉnh xuống đáy.
- S: là diện tích của đáy khối chóp.
Công thức này mang tính chất tổng quát, có thể áp dụng linh hoạt cho mọi loại khối chóp. Việc xác định chính xác diện tích đáy và chiều cao là yếu tố quan trọng để tính đúng thể tích trong các bài toán hình học không gian.
Sử dụng laptop sẽ giúp việc học trở nên hiệu quả và dễ dàng hơn. Với sự đa dạng về sản phẩm, học sinh và sinh viên có thể lựa chọn được mẫu laptop phù hợp với nhu cầu của mình. Dưới đây là một số gợi ý về các mẫu laptop có giá cả phải chăng:
Tổng hợp các dạng bài tập áp dụng công thức tính thể tích khối chóp
Khi đã hiểu rõ các công thức tính thể tích nhanh của khối chóp đều và không đều, việc vận dụng vào bài tập thực tế sẽ giúp bạn hiểu sâu hơn. Dưới đây, Mytour đã chọn lọc 12 dạng bài tập thường gặp, mỗi bài đều có lời giải chi tiết kèm theo:
Dạng 1: Tính thể tích khối chóp có mặt bên vuông góc với mặt đáy
Đề bài: Tính thể tích của khối chóp S.ABCD với mặt (SAB) vuông góc với mặt đáy ABCD hình chữ nhật. Biết rằng AB = 6cm, BC = 8cm và SA = 10cm.
Lời giải:
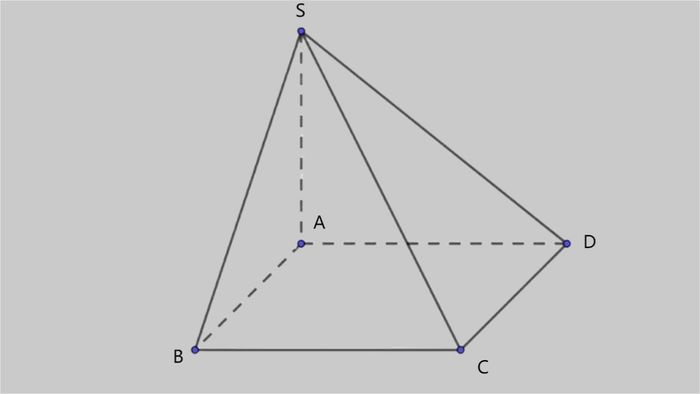
Diện tích đáy tính theo công thức: S = AB x BC = 6 x 8 = 48 cm2
Chiều cao của khối chóp: h = SA = 10cm
Áp dụng công thức tính thể tích cho khối chóp:
V = 1/3 x S x h = 1/3 x 48 x 10 = 160 cm3
Exercise 2: Calculate the volume of a pyramid when the lateral edge is perpendicular to the base
Problem: Find the volume of pyramid S.ABC, given that the base is a right triangle ABC with a right angle at A, AB = AC = 6cm, and the lateral edge SA = 9cm, which forms a 90-degree angle with the base.
Solution:
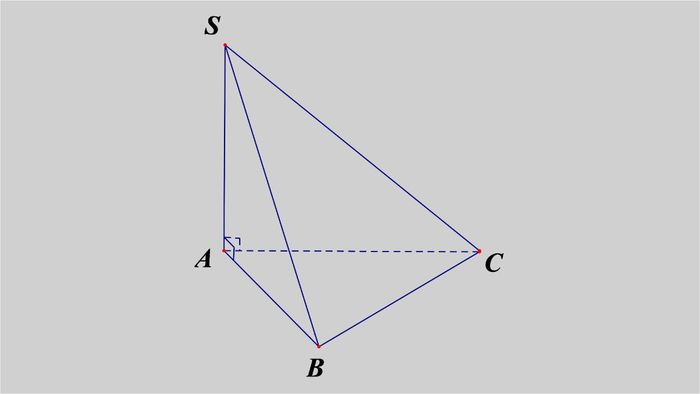
Area of the base: S = 1/2 x AB x AC = 1/2 x 6 x 6 = 18 cm2
Height: h = SA = 9 cm
The volume of the pyramid: V = 1/3 x S x h = 1/3 x 18 x 9 = 54 cm3
Exercise 3: Calculating the volume of pyramid S.ABCD when the base is a square
Problem: Calculate the volume of pyramid S.ABCD with a square base of side length 6 cm and height h = 10 cm.
Solution:
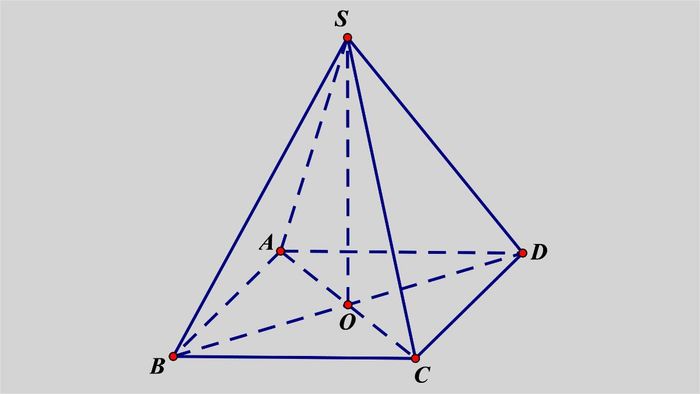
The height h = 10 cm
Base area: S = 6 x 6 = 36 cm2
Applying the formula to calculate the volume of the pyramid:
V = 1/3 x S x h = 1/3 x 36 x 10 = 120 cm3
Case 4: Calculating the volume of a pyramid with a cubic shape
This pyramid has all its side faces as squares, each with 12 equal edges. Therefore, the formula for calculating the volume of this pyramid is: V = a x a x a = a^3 (where a is the edge of the cube).
Problem: Calculate the volume of a pyramid with a cubic shape and an edge length of 6 cm.
Solution:
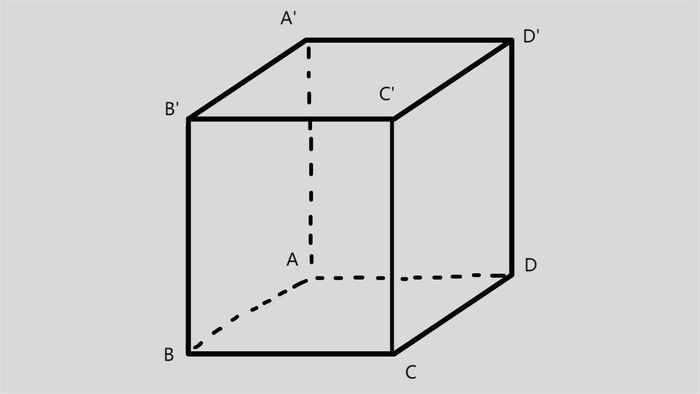
V = a x a x a = a^3 = 6^3 = 216 cm3
Case 5: Volume formula for a pyramid of an equilateral triangular prism
Problem: Calculate the volume of pyramid ABC.A’B’C’ with height h = 9 cm and the base being an equilateral triangle with side length a = 4 cm.
Solution:
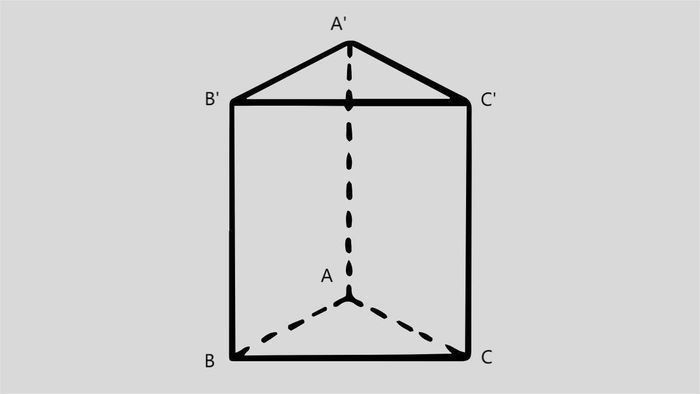
The area of the equilateral triangle base: S = (a^2 x √3)/4 = (4^2 x √3)/4 = 4√3 cm2
Height h = 9 cm
Formula to calculate the volume of a pyramid with an equilateral triangular prism base:
V = S x h = 4√3 x 9 = 36√3 cm3
Case 6: Calculate the volume of a pyramid with a regular hexagonal base
Problem: Calculate the volume of a pyramid with height h = 15 cm and a regular hexagonal base with side length a = 4 cm.
Solution:
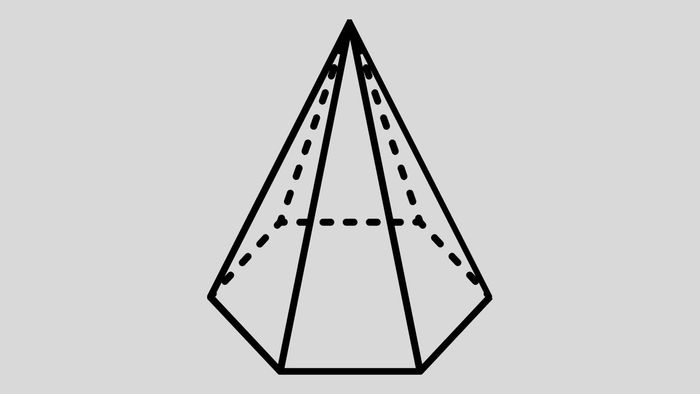
Diện tích đáy lục giác đều: S = (3√3 x a^2)/2 = (3√3 x 4^2)/2 = 24√3 cm2
Chiều cao của khối chóp là h = 15cm
Áp dụng công thức tính thể tích cho khối chóp:
V = 1/3 x S x h = 1/3 x 24√3 x 15 = 120√3 cm3
Dạng 7: Công thức tính thể tích khối chóp thuộc lăng trụ
Đề bài: Tính thể tích của khối chóp lăng trụ ABCD.A’B’C’D’ với AA’ = 5cm, AB = 1cm, BC = 3cm, đáy là hình chữ nhật.
Lời giải:
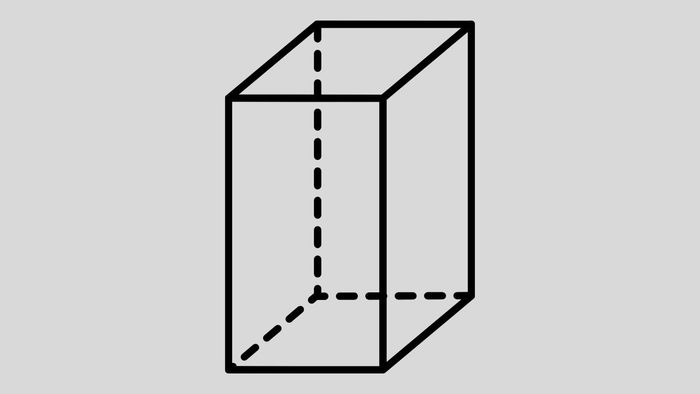
Chiều cao của khối chóp là h = AA’ = 5 cm
Diện tích đáy: S = 1 x 3 = 3 cm2
Công thức tính thể tích khối chóp đối với dạng lăng trụ:
V = B x h = 3 x 5 = 15 cm3 (h: chiều cao, B: diện tích đáy)
Dạng 8: Tính thể tích khối chóp khi đã biết độ dài ba cạnh bên
Đề bài: Tính thể tích của khối chóp S.ABC với SA = 8cm, SB = 10cm, SC = 12cm, và SA vuông góc với mặt đáy tam giác ABC vuông tại A.
Giải pháp:
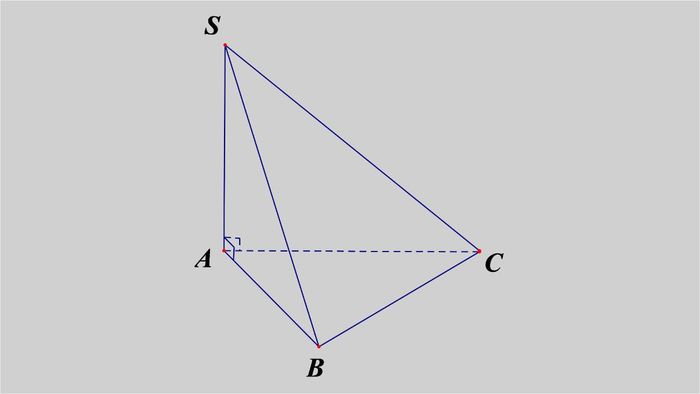
Ta có: SA vuông góc với mặt đáy
Vậy ta kết luận: SA vuông góc với các cạnh AB và AC
Tam giác SAB vuông tại đỉnh A:
AB = √(SB^2 - SA^2) = √(10^2 - 8^2) = 6 cm
Tam giác SAC vuông tại đỉnh A:
AC = √(SC^2 - SA^2) = √(12^2 - 8^2) = 4√5 cm
Diện tích đáy: S = 1/2 x AB x AC = 1/2 x 6 x 4√5 = 12√5 cm²
Chiều cao h = SA = 8 cm
Thể tích khối chóp: V = 1/3 x S x h = 1/3 x 12√5 x 8 = 32√5 cm³
Dạng 9: Tính thể tích khối chóp với các cạnh vuông góc nhau
Đề bài: Tính thể tích khối chóp S.ABC khi các cạnh bên tạo góc vuông với nhau tại S. Biết SA = 5 cm, SB = 3 cm, SC = 4 cm.
Lời giải:
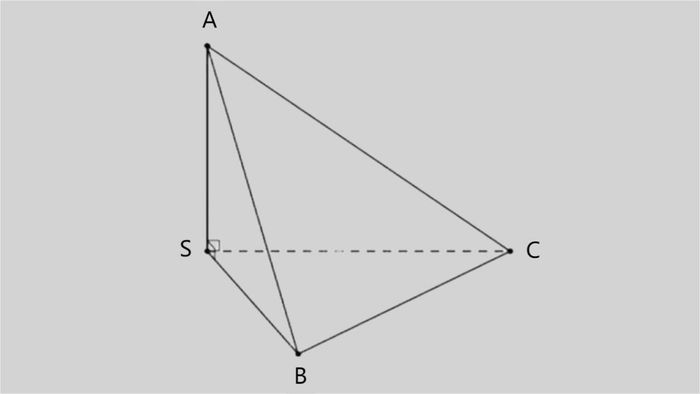
Ta có:
- SA vuông góc với SB
- SA vuông góc với SC
Suy ra: SA vuông góc với mặt (SBC)
Chiều cao h = SA = 5 cm
Diện tích đáy: S = 1/2 x SB x SC = 1/2 x 3 x 4 = 6 cm²
Thể tích của khối chóp: V = 1/3 x S x h = 1/3 x 6 x 5 = 10 cm³
Dạng 10: Tính thể tích của khối chóp tròn xoay
Đề bài: Tính thể tích khối chóp tròn xoay với đáy là một hình tròn có bán kính 7cm và chiều cao 15cm.
Lời giải:
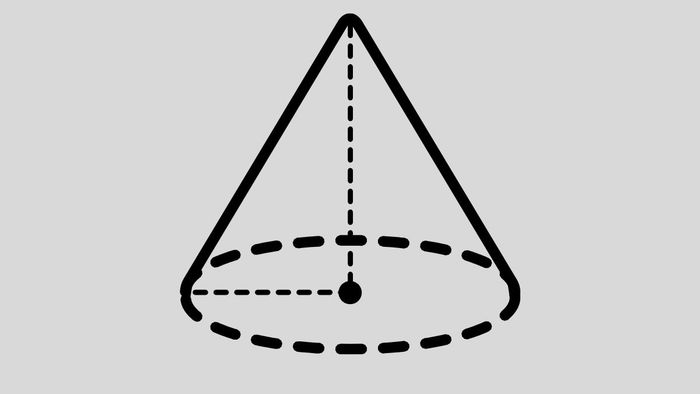
Chiều cao của khối chóp là h = 15cm
Bán kính đáy là r = 7cm
Công thức tính thể tích của khối chóp tròn xoay:
V = 1/3 x B x h = 1/3 x π x r^2 x h = 1/3 x π x 7^2 x 15 = 769,69 cm³
Trong đó:
- B: diện tích của đáy
- r: bán kính của đáy
- h: chiều cao của khối chóp
Dạng 11: Tính thể tích khối chóp có đáy là tam giác đều
Đề bài: Tính thể tích của khối chóp S.ABC có chiều cao h = 9cm và đáy là tam giác đều với mỗi cạnh dài 6cm.
Lời giải:
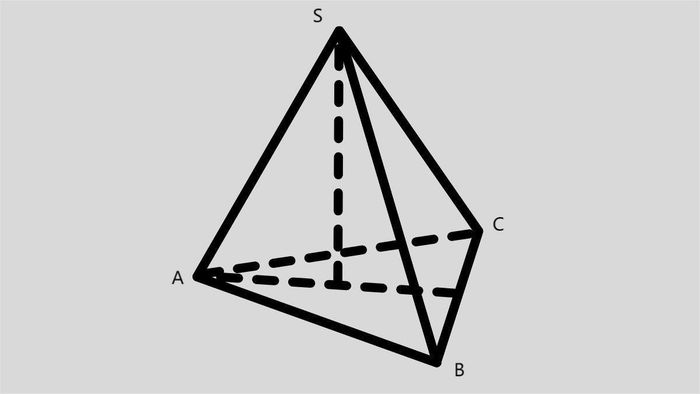
Diện tích đáy: S = (cạnh^2 x √3)/4 = (6^2 x √3)/4 = 9√3 cm2
Chiều cao h = 9 cm
Áp dụng công thức tính thể tích khối chóp:
V = 1/3 x S x h = 1/3 x 9√3 x 9 = 27√3 cm3
Dạng 12: Tính thể tích khối chóp tứ giác đều với cạnh đáy là a
Đề bài: Tính thể tích khối chóp S.ABCD với chiều cao h = 12cm và đáy là hình vuông có cạnh a = 8cm.
Lời giải:
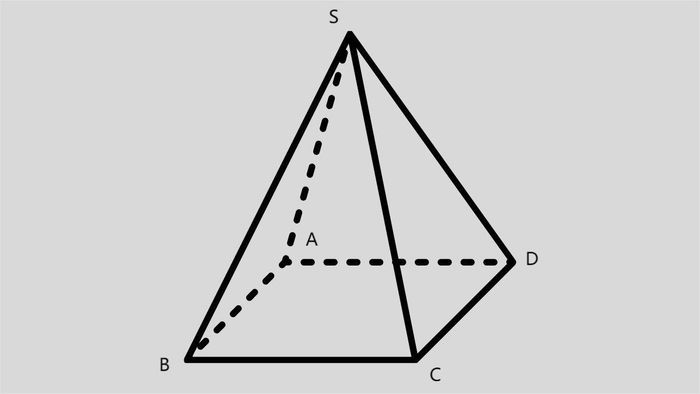
Diện tích đáy: S = a² = 8 x 8 = 64 cm²
Chiều cao h = 12 cm
Công thức tính thể tích khối chóp:
V = 1/3 x S x h = 1/3 x 64 x 12 = 256 cm³
Mytour đã chia sẻ các công thức tính thể tích khối chóp nhanh chóng và đầy đủ, bao gồm các dạng bài tập có lời giải chi tiết. Việc nắm vững công thức tính thể tích khối chóp giúp bạn không chỉ nâng cao thành tích học tập mà còn phát triển khả năng tư duy hình học.
