Khối lăng trụ là gì? Cách tính thể tích khối lăng trụ như thế nào? Đây là câu hỏi mà nhiều bạn học sinh quan tâm đến. Hãy cùng theo dõi bài viết dưới đây để có câu trả lời nhé.
Trong bài học này, chúng tôi sẽ giới thiệu đến các bạn toàn bộ kiến thức về hình lăng trụ, cách tính thể tích của khối lăng trụ cùng với một số bài tập minh họa kèm đáp án chi tiết. Hy vọng rằng đây sẽ là tài liệu hữu ích, giúp các bạn củng cố kỹ năng giải toán và đạt được điểm cao trong các bài kiểm tra và kỳ thi sắp tới. Ngoài ra, bạn cũng có thể xem thêm về cách tính chu vi của hình chữ nhật và diện tích của hình vuông.
Thể tích của khối lăng trụ: Công thức và bài tập
1. Khái niệm về hình lăng trụ
Một đa giác có hai mặt đáy song song và bằng nhau, mặt bên là hình bình hành thì được gọi là hình lăng trụ.
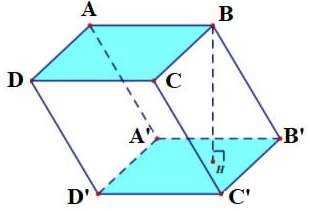
Tên gọi của hình lăng trụ
Hình lăng trụ được đặt tên dựa trên mặt đáy của nó.
Ví dụ:
- Nếu mặt đáy của hình lăng trụ là hình tam giác đều thì được gọi là hình lăng trụ tam giác đều.
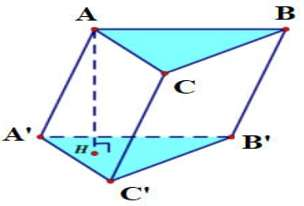
- Nếu hình tứ giác đều là mặt đáy, ta gọi đó là hình lăng trụ tứ giác đều.
Hình lăng trụ đứng
Khi các cạnh bên của hình lăng trụ tạo vuông góc với mặt đáy, nó được gọi là hình lăng trụ đứng.
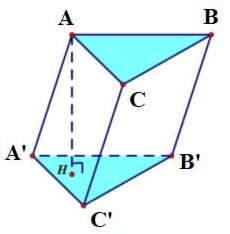
Chú ý:
- Khi mặt đáy là hình chữ nhật, hình lăng trụ đứng của tứ giác còn được biết đến với tên gọi khác là hình hộp chữ nhật.
- Nếu hình trụ đứng tứ giác có 12 cạnh đều có độ dài là a, ta gọi nó là hình lập phương.
2. Một số dạng lăng trụ
a) Hình lăng trụ đứng: là hình lăng trụ có các cạnh bên vuông góc với đáy. Chiều dài cạnh bên được gọi là chiều cao của hình lăng trụ. Lúc này, các mặt bên của hình lăng trụ đứng là các hình chữ nhật.
b) Hình lăng trụ đều: là hình lăng trụ đứng có đáy là đa giác đều. Các mặt bên của lăng trụ đều là các hình chữ nhật bằng nhau. Ví dụ: hình lăng trụ tam giác đều, tứ giác đều... được hiểu là hình lăng trụ đều.
c) Hình hộp: Là hình lăng trụ có đáy là hình bình hành.
d) Hình hộp đứng: là hình lăng trụ đứng có đáy là hình bình hành
e) Hình hộp chữ nhật: là hình hộp đứng có đáy là hình chữ nhật
f) Hình lăng trụ đứng: có đáy là hình vuông và các mặt bên đều là hình vuông được gọi là hình lập phương (hay hình chữ nhật có ba kích thước bằng nhau được gọi là hình lập phương)
Nhận xét:
- Hình hộp chữ nhật là hình lăng trụ đứng (Có tất cả các mặt là hình chữ nhật
- Hình lập phương là hình lăng trụ đều (tất cả các cạnh bằng nhau)
- Hình hộp đứng là hình lăng trụ đứng (mặt bên là hình chữ nhật, mặt đáy là hình bình hành)
3. Thể tích của khối lăng trụ đứng
Công thức tính thể tích khối lăng trụ đứng:
V = S * h
Trong đó:
- S là diện tích đáy
- h là chiều cao của khối lăng trụ.
Lưu ý: Lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.
4. Ví dụ tính thể tích của khối lăng trụ
Ví dụ 1:
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a = 2 cm và chiều cao là h = 3 cm. Hãy tính thể tích của hình lăng trụ này?
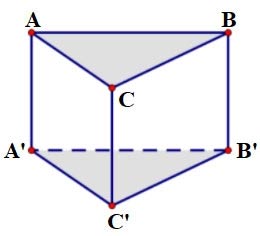
Giải:

Khi đó, thể tích của khối lăng trụ là:

Ví dụ 2:
Cho hình hộp đứng có các cạnh AB = 3a, AD = 2a, AA’= 2a. Tính thể tích của khối A’.ACD’
Hướng dẫn:
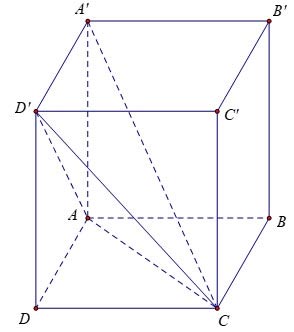
Vì mặt bên ADD’A’ là hình chữ nhật nên ta có:




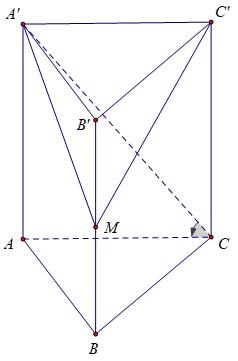
Ví dụ 3: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a√3, góc giữa và đáy là 60º. Gọi M là trung điểm của BB'. Tính thể tích của khối chóp M.A’B’C’.
Giải:







Ví dụ 4:
Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a và mặt (DBC’) với đáy ABCD tạo một góc 60º. Tính thể tích khối lăng trụ ABCD.A’B’C’D?
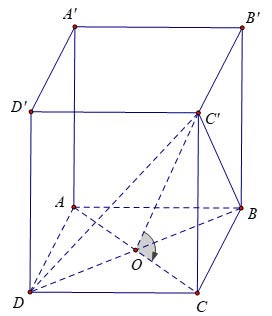


)
%2C(ABCD))%20%3D%20%E2%88%A0(C%27OD)%20%3D%2060%C2%BA)
Lại có:





5. Bài tập thể tích khối lăng trụ
Bài 1. Một bể nước hình trụ có diện tích mặt đáy B = 2 m2 và đường cao h = 1 m. Thể tích của bể nước này bằng bao nhiêu?
Lời giải
Áp dụng công thức V = B.h = 2.1 = 2 m3.
Bài 2:










Câu 3: Cho hình lăng trụ tứ giác đều có tất cả các cạnh bằng a. Thể tích khối lăng trụ này:




Câu 4 Cho lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh bên bằng 4a và đường chéo 5a. Tính thể tích của khối lăng trụ này là:



 Câu 5:
Câu 5:



 Câu 6
Câu 6



 Câu 7
Câu 7




Hãy tham khảo thêm các bài tập về thể tích khối lăng trụ để nắm vững công thức tính thể tích này nhé.
