1. Tứ diện là gì? Tứ diện đều là gì?
Tứ diện là một hình học không gian với bốn đỉnh thường ký hiệu là A, B, C, và D. Mỗi đỉnh trong số các điểm A, B, C, và D đều có thể coi là đỉnh của tứ diện. Mặt đối diện với điểm D được gọi là mặt đáy. Ví dụ, nếu chọn B làm đỉnh của tứ diện thì mặt đáy sẽ là ACD.
Tóm gọn, nếu trong không gian có 4 điểm không nằm trên cùng một mặt phẳng là A, B, C, và D, thì hình đa diện với các đỉnh này gọi là khối tứ diện. Được ký hiệu là ABCD.
- Tứ diện đều được định nghĩa là tứ diện có tất cả các mặt bên là tam giác đều, và nó thuộc vào nhóm năm khối đa diện đều.
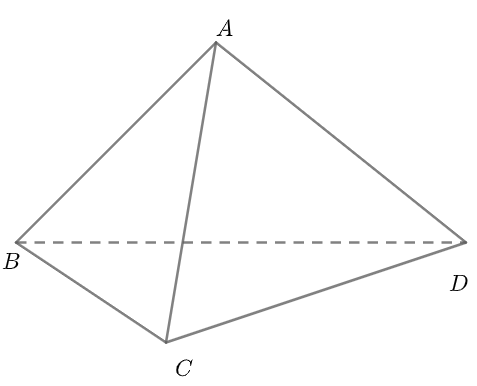
Những đặc điểm nổi bật của tứ diện đều:
Tứ diện đều sở hữu các đặc điểm sau:
- Tất cả bốn mặt xung quanh đều là các tam giác đều có kích thước như nhau
- Các mặt của tứ diện đều là các tam giác với ba góc nhọn đều nhau
- Tổng các góc tại bất kỳ đỉnh nào của tứ diện đều bằng 180 độ
- Các cặp cạnh đối diện trong tứ diện đều có chiều dài giống nhau
- Các mặt của tứ diện đều có kích thước giống nhau
- Các đường cao của tứ diện đều có độ dài đồng nhất
- Tâm của các mặt tiếp xúc và ngoại tiếp tứ diện trùng với tâm của tứ diện
- Hình hộp ngoại tiếp tứ diện có dạng hình hộp chữ nhật
- Các góc phẳng tương ứng với mỗi cặp cạnh đối diện của tứ diện bằng nhau
- Đoạn thẳng nối các trung điểm của các cạnh đối diện là đường vuông góc với cả hai cạnh đó
- Tứ diện có ba trục đối xứng
- Tổng các cosin của các góc phẳng nằm trên cùng một mặt của tứ diện bằng 1
2. Công thức tính thể tích của tứ diện đều với cạnh a
Tứ diện đều với cạnh a là một tứ diện trong đó tất cả các cạnh đều có độ dài bằng a
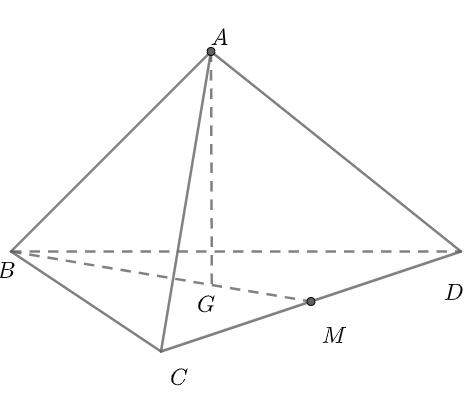
Khi giải bài toán về tứ diện đều, cần chú ý cách vẽ. Để vẽ tứ diện đều ABCD, bạn có thể thực hiện theo các bước sau:
- Xem tứ diện đều như một hình chóp với đáy là tam giác đều, ví dụ như A. BCD
- Vẽ mặt đáy, chẳng hạn như mặt BCD
- Vẽ một đường trung tuyến của mặt đáy BCD, ví dụ BM là trung tuyến của tam giác BCD
- Xác định trọng tâm G của tam giác BCD, và G sẽ là tâm của mặt đáy.
Dựng đường cao (đường thẳng đi qua G và song song với mặt phẳng giấy hoặc bề mặt làm việc của bạn)
Chọn điểm A trên đường vừa dựng và hoàn tất việc vẽ hình
Bài toán: Tính thể tích của khối tứ diện có cạnh a
Giải pháp:
Giả sử ABCD là tứ diện đều với cạnh a. G là trọng tâm của tam giác BCD như đã vẽ ở trên
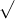
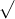
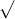
Vì vậy, thể tích của khối tứ diện đều với cạnh a được tính bằng:
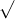
Một tứ diện đều có 6 cạnh bằng nhau và 4 mặt đều là tam giác đều, với các công thức tính thể tích như sau:
- Thể tích của tứ diện ABCD được tính bằng một phần ba tích của diện tích mặt đáy và chiều cao từ mặt đáy đó, cụ thể là: V = 1/3 x A (BCD) x AH
- Thể tích của tứ diện đều với mặt đáy là tam giác ABC được tính bằng một phần ba tích diện tích mặt đáy và chiều cao từ đáy đến đỉnh, công thức là: V = 1/3 x B x h
Do đó, thể tích của tứ diện đều với cạnh a được tính bằng công thức:
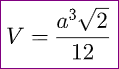
3. Bài tập thực hành để luyện tập
Câu 1: Tính thể tích của khối chóp tứ diện đều có cạnh a:
A. a³/3
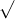
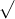
Câu 2: Hình tứ diện đều có tổng số mặt phẳng đối xứng là
A. 4 mặt phẳng đối xứng
B. 6 mặt phẳng đối xứng
C. 8 mặt phẳng đối xứng
D. 10 mặt phẳng đối xứng
Câu 3: Các điểm trung điểm của các cạnh trong một tứ diện đều tạo thành hình gì?
A. các đỉnh của một hình đa diện 20 mặt đều
B. các đỉnh của một hình đa diện 12 mặt đều
C. các đỉnh của một hình bát diện đều
D. các đỉnh của một tứ diện đều
Câu 4: Xét khối chóp tam giác đều S. ABC với cạnh đáy bằng a và cạnh bên đáy. Tính thể tích V của khối chóp S.ABC theo a
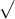
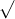
Câu 6: Với tứ diện đều ABCD có thể tích là 12 và G là trọng tâm của tam giác BCD, tính thể tích của khối chóp A. GBC
A. V = 4
B. V = 3
C. V = 5
D. V = 6
Câu 7: Tính thể tích của khối tứ diện đều ABCD với các thông số sau:
a. Cạnh AB = 4 cm
b. Cạnh CD = 6 cm
c. Cạnh BD = 3 cm
Hướng dẫn giải bài toán:
a. Vì là tứ diện đều, tất cả các cạnh đều bằng nhau: BC = CD = BD = AC = AB = 4 cm, do đó thể tích được tính như sau:
Cho tứ diện đều ABCD với cạnh a = 5 cm. Hãy tính thể tích của nó.
b. Trong tứ diện đều, các cạnh đều bằng: AB = DA = BD = AC = CD = 6 cm, và thể tích là:
c. Tứ diện đều có các cạnh bằng nhau: AB = BC = DA = AC = BD = 3 cm, và thể tích được tính như sau:
Câu 8: Cho hình chóp đều S> ABCD, với đáy là hình vuông và đường SA vuông góc với mặt phẳng ABC. Xác định các mặt đối xứng của hình chóp này.
Câu 9: Tính góc tạo bởi hai đoạn thẳng AB và CD trong một tứ diện đều ABCD với cạnh a.
Câu 10: Trong tứ diện đều ABCD với cạnh a, kéo dài đoạn BC thêm một đoạn CE = a và đoạn BD thêm một đoạn DF = a. M là trung điểm của AB.
a. Xác định thiết diện của tứ diện với mặt phẳng (MÈ).
b. Tính diện tích của thiết diện đó theo cạnh a.
Câu 11: Trong hình chóp đều S với đáy là hình vuông ABCD và đường SA vuông góc với mặt phẳng (ABCD), hãy xác định các mặt đối xứng của hình chóp này.
Câu 12. Khi hình tứ diện ABCD được viết dưới dạng D. ABC, chúng ta có thể kết luận điều gì?
A. Hình tứ diện ABCD có thể coi là hình chóp tam giác D. ABC với đỉnh là D.
B. Hình tứ diện ABCD có thể coi là hình chóp tam giác D. ABC với mặt đáy là mặt phẳng (ABC).
C. Hình tứ diện ABCD có thể coi là hình chóp tam giác D. ABC, và thể tích của nó được tính bằng diện tích tam giác ABC nhân với khoảng cách từ đỉnh D đến mặt phẳng (ABC) chia cho 3.
D. Các kết luận A, B và C đều đúng.
Câu 13. Với hình tứ diện ABCD có thể tích là 9a³ và diện tích tam giác BCD là 3a², phát biểu nào sau đây là chính xác?
A. Khoảng cách từ đỉnh A đến mặt phẳng BCD là 3a.
B. Khoảng cách từ đỉnh A đến mặt phẳng BCD là 9a.
C. Khoảng cách từ đỉnh A đến mặt phẳng BCD là 6a.
D. Khoảng cách từ đỉnh A đến mặt phẳng BCD là a.
Câu 14: Tính thể tích của tứ diện ABCD khi khoảng cách từ đỉnh D đến mặt phẳng (ABC) là 4a và diện tích tam giác ABC là 12a².
A. Thể tích của tứ diện ABCD là 3a³.
B. Thể tích của tứ diện ABCD là 16a³.
C. Thể tích của tứ diện ABCD là 48a³.
D. Thể tích của tứ diện ABCD là 12a³.
Câu 15: Trong một tứ diện đều, ta có các đặc điểm sau:
A. Tất cả các cạnh đều có độ dài giống nhau
B. Tất cả các mặt đều có diện tích giống nhau
C. Cả A và B đều không chính xác
D. Cả A và B đều đúng
Bài viết trên Mytour đã cung cấp thông tin chi tiết về cách tính thể tích tứ diện đều với cạnh a và các bài tập thực hành. Bài viết cũng đã nêu rõ đáp án và lý thuyết liên quan. Xin cảm ơn bạn đọc đã theo dõi bài viết.
