1. Công thức giải nhanh Toán lớp 11 Chương 1: Đại số
1.1 Hàm số lượng giác
Hàm số y = sinx
- Tập xác định: -1 ≤ sinx ≤ 1
- Đây là hàm số lẻ
- Hàm số tuần hoàn với chu kỳ là 2π
- Hàm số đồng biến trên đoạn
- Hàm số nghịch biến trên đoạn
.png)
Hàm số y = cosx
- Định nghĩa miền xác định: -1 ≤ sinx ≤ 1
- Hàm số là hàm số chẵn
- Hàm số tuần hoàn với chu kỳ 2π
- Hàm số có tính đồng biến trên khoảng (-π + k2π ; k2π)
- Hàm số có tính nghịch biến trên khoảng (k2π ; π + k2π)
.png)
Hàm số y = tanx
- Miền xác định:
- Hàm số là hàm số lẻ
- Hàm số có chu kỳ tuần hoàn bằng π
- Hàm số có tính đồng biến trên một số khoảng nhất định
- Hàm số có các đường tiệm cận đặc trưng
.png)
Hàm số y = cotx
- Miền xác định:
- Hàm số thuộc loại lẻ
- Hàm số có chu kỳ tuần hoàn là π
- Hàm số có tính nghịch biến trên khoảng (kπ ; π + kπ)
- Các đường tiệm cận của hàm số là x = kπ
.png)
1.2 Giá trị lượng giác của các cung
có liên hệ đặc biệt với nhau.
- Các cung đối nhau là: α và -α
cos(-α) = cos α
sin(-α) = -sin α
tan(-α) = -tan α
cot(-α) = -cot α
- Các cung bù nhau là: α và π - α
sin(π - α) = sin α
cos(π - α) = -cos α
tan(π - α) = -tan α
cot(π - α) = -cot α
- Các cung chênh lệch π: α và (α + π)
sin(α + π) = -sin α
cos(α + π) = -cos α
tan(α + π) = tan α
cot(α + π) = cot α
- Các cung phụ nhau: α và
→ Cos đối nhau, sin bù nhau, tan và cot hơn kém π, phụ chéo.
+) Các cung chênh lệch:
1.3 Công thức lượng giác
+) Công thức cộng
cos(a - b) = cos a cos b + sin a sin b
cos(a + b) = cos a cos b - sin a sin b
sin(a - b) = sin a cos b - cos a sin b
sin(a + b) = sin a cos b + cos a sin b
+) Công thức nhân đôi
sin 2a = 2 sin a cos a
cos 2a = cos²a - sin²a = 2cos²a - 1 = 1 - 2sin²a
+) Công thức nhân ba
sin 3a = 3 sin a - 4 sin³a
cos 3a = 4 cos³a - 3 cos a
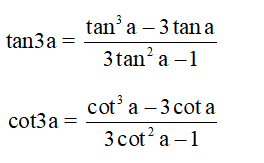
+) Công thức hạ bậc
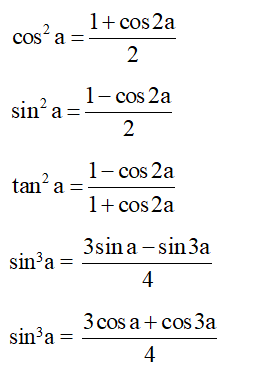
+) Các hệ quả liên quan
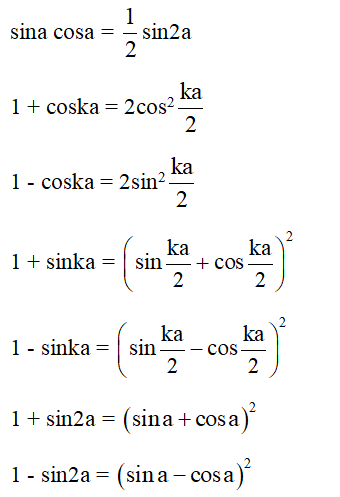
+) Công thức chuyển đổi tích thành tổng
.png)
+) Công thức chuyển đổi tổng thành tích:
.png)
+) Đặc biệt khi a = b = α
.png)
1.4 Phương trình lượng giác
Các phương trình lượng giác cơ bản
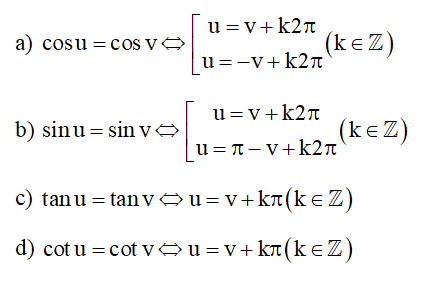
Đặc biệt:
.png)
Phương trình bậc hai đối với hàm số lượng giác
.png)
Tìm nghiệm t phù hợp rồi áp dụng vào phương trình cơ bản
Lưu ý: cos2x = 2cos2x - 1 = 1 - 2sin2x = cos2x - sin2x
sin2x = 1 - cos2x
cos2x = 1 - sin2x
Phương trình bậc nhất với sinx và cosx
- Hình thức phương trình: asinx + bcosx = c
- Điều kiện để phương trình có nghiệm: a2 + b2 ≥ c2
- Cách giải: Chia cả hai vế của phương trình cho một hệ số, sau đó áp dụng công thức cộng để chuyển về dạng phương trình cơ bản.
Phương trình bậc hai với sin(u) và cos(u)
Dạng phương trình: asin2u + bsinu.cosu + c.cos2u = d
Cách giải
+ Kiểm tra xem cosu = 0 có thỏa mãn phương trình không?
Xem xét trường hợp
Thay cosu = 0 vào phương trình (nhớ rằng sin2u = 1)
+ Xem xét trường hợp
Chia hai vế của phương trình cho , sau đó giải phương trình theo .
Ghi chú: Có thể sử dụng công thức hạ bậc để đưa về dạng asin2u + bcos2u = c.
Phương trình đối xứng và phản xứng
- Phương trình với các biểu thức chứa sinu ± cosu và sản phẩm sinu.cosu
Hướng dẫn cách giải chi tiết:
.png)
Thay vào phương trình ban đầu để chuyển đổi thành phương trình bậc hai theo biến t.
Một số lưu ý quan trọng:
.png)
2. Công thức giải nhanh Đại số lớp 11 Chương 2
2.1 Đại số tổ hợp
Quy tắc cộng
Phân chia công việc thành hai trường hợp khác nhau:
- Trường hợp 1: có m cách thực hiện.
- Trường hợp 2: có n cách thực hiện.
Vậy tổng số cách thực hiện là .
Quy tắc nhân
Sự vật 1 có m cách chọn. Đối với mỗi cách chọn của sự vật 1, có n cách chọn cho sự vật 2.
Tổng số cách chọn liên tiếp 2 sự vật là mn.
Giai thừa
n! = 1.2.3... (n - 1)n
Qui ước: 0! = 1
Lưu ý:
n! = (n - 1)!n = (n - 2)!(n - 1)n = ...
Hoán vị
Số cách sắp xếp n vật vào n chỗ là: Pn = n!
Chỉnh hợp
Với n vật, khi chọn ra k vật và sắp xếp chúng, số cách sắp xếp là:
.png)
Tổ hợp
Khi chọn ra k vật từ n vật mà không quan tâm đến thứ tự, số cách chọn là:
.png)
Một số kiến thức quan trọng cần ghi nhớ
Số chia hết cho 2 nếu chữ số cuối là 2, 4, 6, hoặc 8
Số chia hết cho 5 nếu chữ số cuối là 0 hoặc 5
Số chia hết cho 10 khi chữ số cuối là 0
Số chia hết cho 100 khi chữ số cuối là 00, 25, 50, hoặc 75
Số chia hết cho 3 nếu tổng các chữ số của nó chia hết cho 3
Số chia hết cho 9 nếu tổng các chữ số của nó chia hết cho 9
Khi làm bài tập với số tự nhiên liên quan đến số 0, cần chia thành các trường hợp khác nhau
+) Các tính chất
.png)
2.2 Nhị thức Newton
Khai triển theo định lý nhị thức Newton
.png)
Những công thức quan trọng cần nhớ
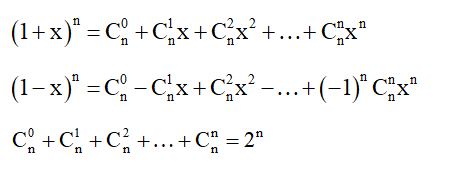
Tam giác Pascal (cung cấp giá trị của các hệ số)
.png)
2.3 Xác suất thống kê
Không gian mẫu ký hiệu là: Ω
Số lượng phần tử trong không gian mẫu được ký hiệu là: n(Ω)
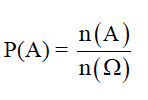
Lưu ý: Xác suất P(A) luôn nằm trong khoảng từ 0 đến 1
2. Nếu A1, A2, …, Ak là các biến cố không có điểm chung thì
P(A1 ∪ A2 ∪ ... ∪ Ak) = P(A1) + P(A2) + ... + P(Ak)
3. Nếu A1, A2, …, Ak là các biến cố độc lập thì
P(A1 ∩ A2 ∩ ... ∩ Ak) = P(A1) × P(A2) × ... × P(Ak)
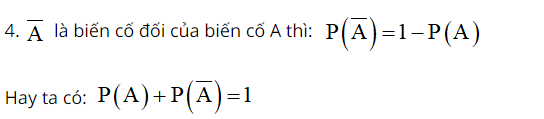
5. X là một biến ngẫu nhiên rời rạc với tập hợp giá trị là {x1; x2;…; xn}
a) Kỳ vọng của X được tính bằng công thức với pi = P(X = xi), i = 1, 2, 3, …, n
b) Phương sai của X được tính bằng công thức hoặc công thức khác, trong đó pi = P(X = xi), i = 1, 2, 3, ..., n và μ = E(X)
c) Độ lệch chuẩn của X được tính như sau:
3. Các công thức giải nhanh Toán lớp 11 Chương 1 về Hình học
3.1 Khái quát về phép biến hình
PBH F: (chuyển điểm M thành một điểm duy nhất M'), ký hiệu M' = F(M)
- Hình H' = F(H) ⇔ H' =
- O = F(O) ⇔ O là điểm không bị thay đổi.
- Phép biến hình mà mỗi điểm trong mặt phẳng được chuyển thành chính nó gọi là phép đồng nhất, ký hiệu .
- (tích của hai phép biến hình bằng cách thực hiện liên tiếp phép biến hình F và G)
3.2 Phép dời hình
Nếu PBH F là phép dời hình và A' = F(A); B' = F(B), thì A'B' = AB (khoảng cách giữa hai điểm được bảo toàn)
Phép dời hình biến
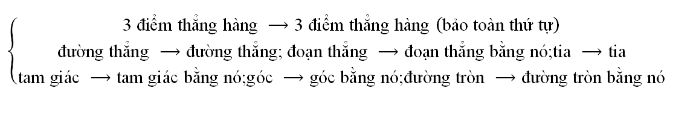
3.3 Phép tịnh tiến theo vector u, ký hiệu T(u)
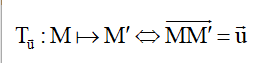
3.4 Phép đối xứng qua trục d, ký hiệu Đd
.png)
Phép đối xứng qua tâm I, ký hiệu ĐI
.png)
3.6 Phép vị tự với tâm I và tỷ số k, ký hiệu V(I;k)
.png)
3.7 Phép đồng dạng (PĐD)
PĐD với tỷ số k (k > 0) là phép biến hình sao cho với hai điểm bất kỳ A và B, và ảnh của chúng là A' và B', ta có A'B' = kAB
PĐD biến

3.8 Biểu thức tọa độ
Giả sử có điểm M(x;y) và M(x';y')
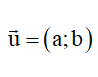
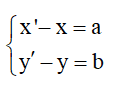
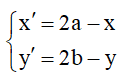
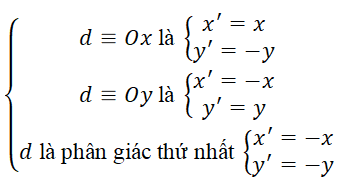
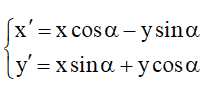
Lưu ý: Khi tâm quay là O(0;0) thì
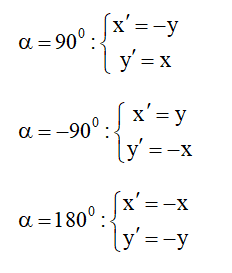
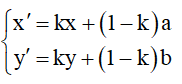
3.9 Ảnh của đường thẳng d khi áp dụng PTT, phép ĐXT, PQ và PVT
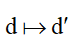
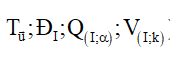
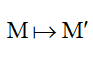
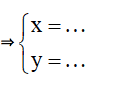
Nếu M thuộc đường thẳng d, thay x và y vào d, ta sẽ có đường thẳng d'.
3.10 Ảnh của đường tròn khi áp dụng các phép biến hình
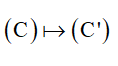
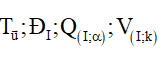
Xác định tâm I của đường tròn (C) và tìm ảnh I' của I qua phép biến hình F.
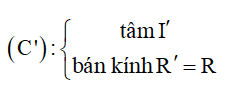
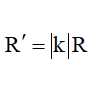
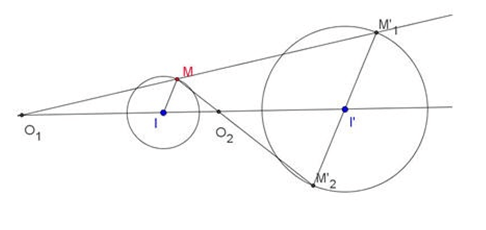
Tâm vị tự của hai đường tròn
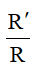
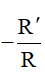
.png)
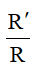
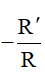
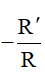
.png)
- Đề thi học kì 1 môn Toán lớp 11 mới nhất cùng đáp án
- Đề thi học kì 2 môn Toán lớp 11 với đáp án
- Đề cương ôn tập học kì 2 môn Toán lớp 11 mới nhất
- Các quy tắc tính xác suất trong Toán lớp 11 và bài tập ứng dụng
